Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 15 september 2018.

Opgave 378 [niveau oOO]

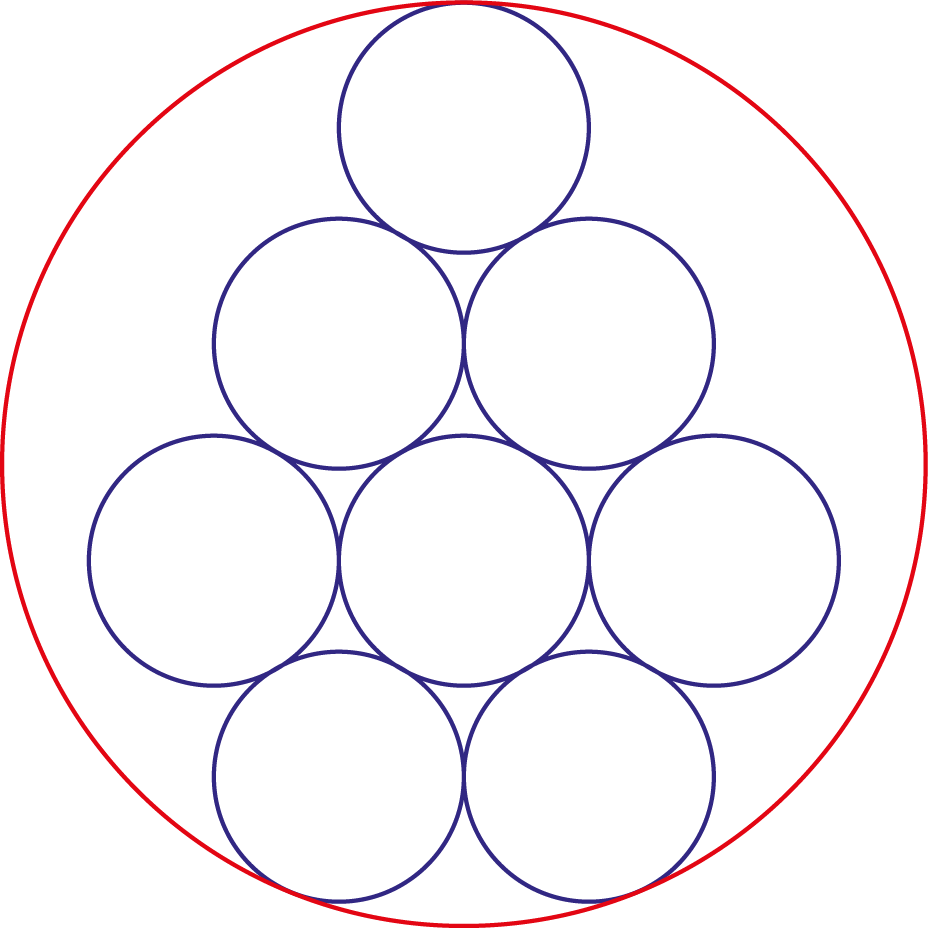
Acht cirkels, elk met straal $\sqrt{3}$ raken elkaar zoals in de figuur te zien is. Een omgeschreven cirkel raakt aan drie van deze cirkels. Hoe groot is de straal van deze omschrijvende cirkel?

Opgave 379 [niveau oOO]

Hoeveel factoren $12$ bevat $2018!$ ? En hoeveel factoren $12$ bevat $2025!$ ? Weet dat $n!$ betekent: $1 \times 2 \times 3 \times … \times n$, dus bijvoorbeeld $4! = 1 \times  2 \times  3 \times 4 = 24$.

Opgave 380 [niveau oOO]

Bewijs: als in drie van de vier hoekpunten van een viervlak de som van de drie hoeken bij zo’n hoekpunt $180°$ is, dan zijn de vier zijvlakken congruente driehoeken.

Opgave 381 [niveau ooO]

Vind alle gehele getallen $n$ waarvoor geldt: $\max(2n – 11 + 2n^6, 2 \max(n – 7 + n^6, 5 – 2n + n^6)) ≤ 2n^6$.
Hierbij staat $\max(a, b)$ voor het maximum, dus de grootste, van de getallen $a$ en $b$. Bijvoorbeeld, $\max(3, 5) = 5$, $\max(-3, -5) = -3$ en $\max(3, 3) = 3$.

Opgave 382 [niveau ooO]

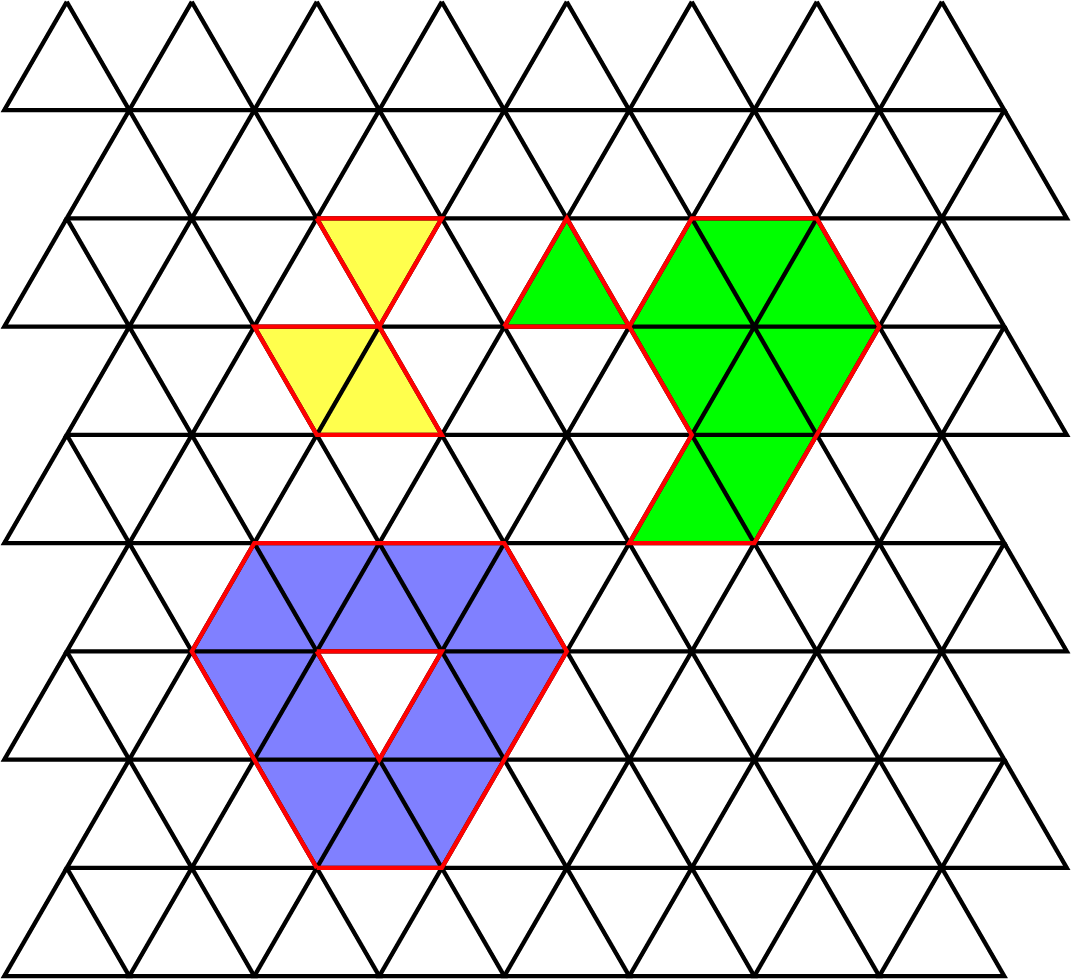
Bijgevoegd is een rooster van gelijkzijdige driehoeken. De $12$ blauwe driehoeken hebben een omtrek van lengte $12$.  De $9$ groene driehoeken hebben een omtrek van $11$. De $3$ gele driehoeken hebben een omtrek van $7$. We vermoeden dat een even aantal driehoeken altijd een even omtrek heeft en een oneven aantal driehoeken altijd een oneven omtrek heeft. Is dat correct? Bewijs dit of geef een tegenvoorbeeld.

Opgave 383 [niveau ooO]

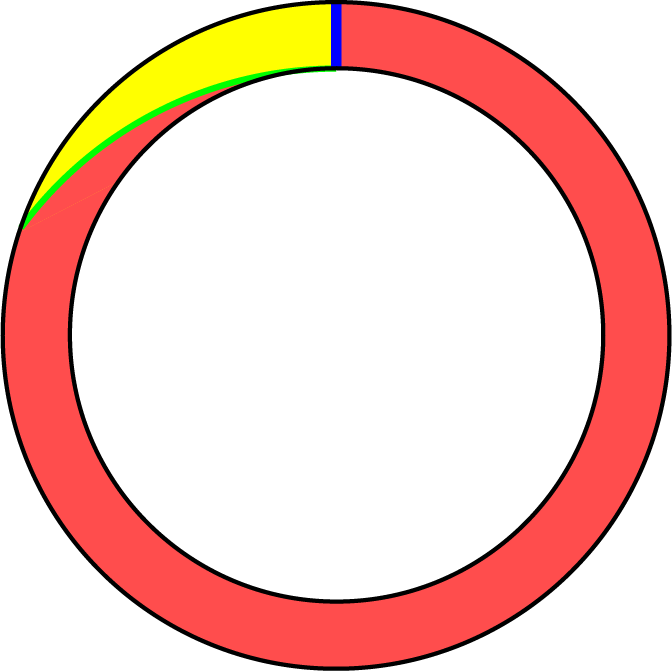
Op een atletiekbaan loopt iedereen een deel van een cirkel. Om precies te zijn lopen ze van het rechte blauwe lijnstuk $A$ met de klok mee naar de groene kromme $B$. Hierbij is de kromme $B$ zo getrokken dat elke deelnemer dezelfde afstand aflegt, waar ze ook beginnen op $A$. Deze afstand is altijd $400 m$. Dit betekent dat het gele stukje tussen $A$ en $B$ nooit gebruikt hoeft te worden. Wat is het oppervlak van dit gele gebiedje, als gegeven is dat de buitenste omtrek van de gehele baan $500 m$ is?

Opgave 384 [niveau ooo] Goed voor drie punten!

We hebben $D(n)$, de som van de cijfers van een natuurlijk getal $n$, en $R(n)$, het omgekeerde van $n$.
Bijvoorbeeld: $D(271) = 2 + 7 + 1 = 10$ en $R(271) = 172$. Bepaal alle natuurlijke getallen $n$ met $D(n) \times R(D(n)) = n$.

Bekijk oplossing