Opgave 378 [oOO]

Acht cirkels, elk met straal $\sqrt{3}$ raken elkaar zoals in de figuur te 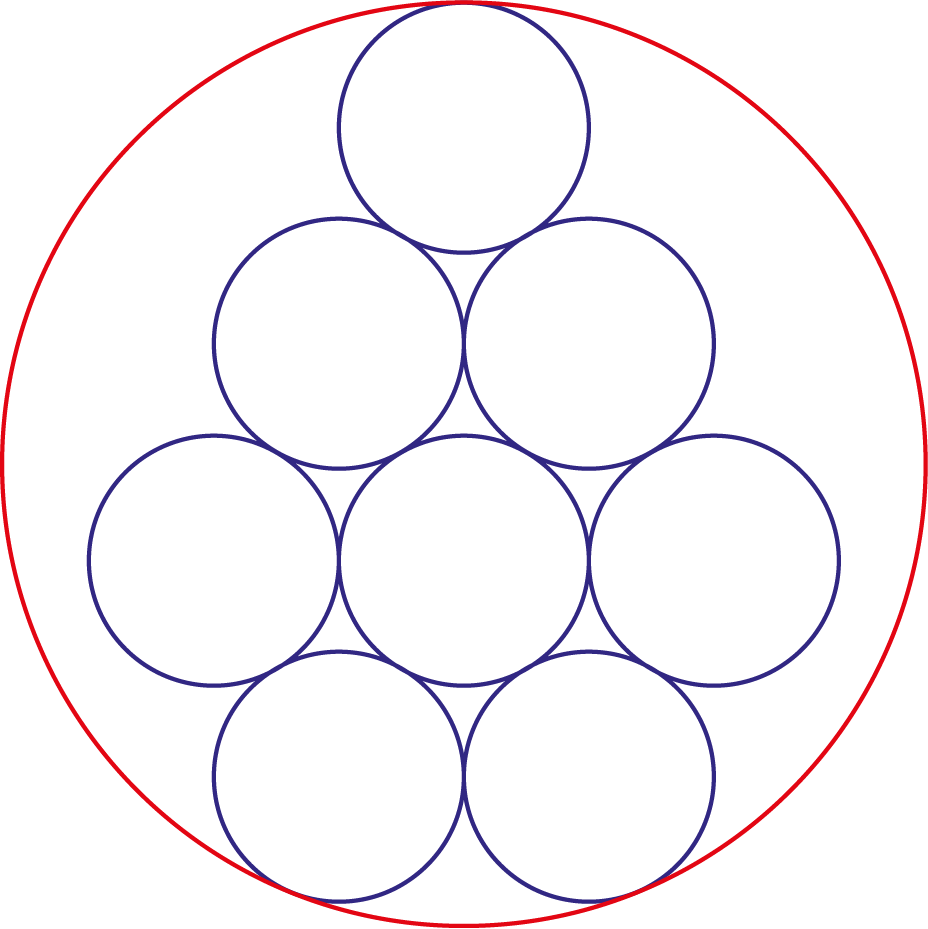zien is. Een omgeschreven cirkel raakt aan drie van deze cirkels. Hoe groot is de straal van deze omschrijvende cirkel?

Oplossing. De middelpunten van de kleine cirkels in de figuur zijn $A$ t/m $H$, het middelpunt van de grote cirkel is $M$, $N$ is het midden van lijnstuk $AB$, de punten waar de kleine en grote cirkels elkaar raken zijn $P$, $Q$ en $R$. In het rood zijn de stralen $MP$, $MQ$ en $MR$ getekend. Omdat zowel de stralen van de kleine cirkel als de straal van de grote cirkel de cirkels loodrecht snijden vallen de stralen daar samen. Zodoende ligt $A$ op $MP$, $B$ op $MQ$ en $C$ op $MR$. We noemen $MA = MB = MC = x$. Uiteindelijk is de gevraagde straal $x + \sqrt3$.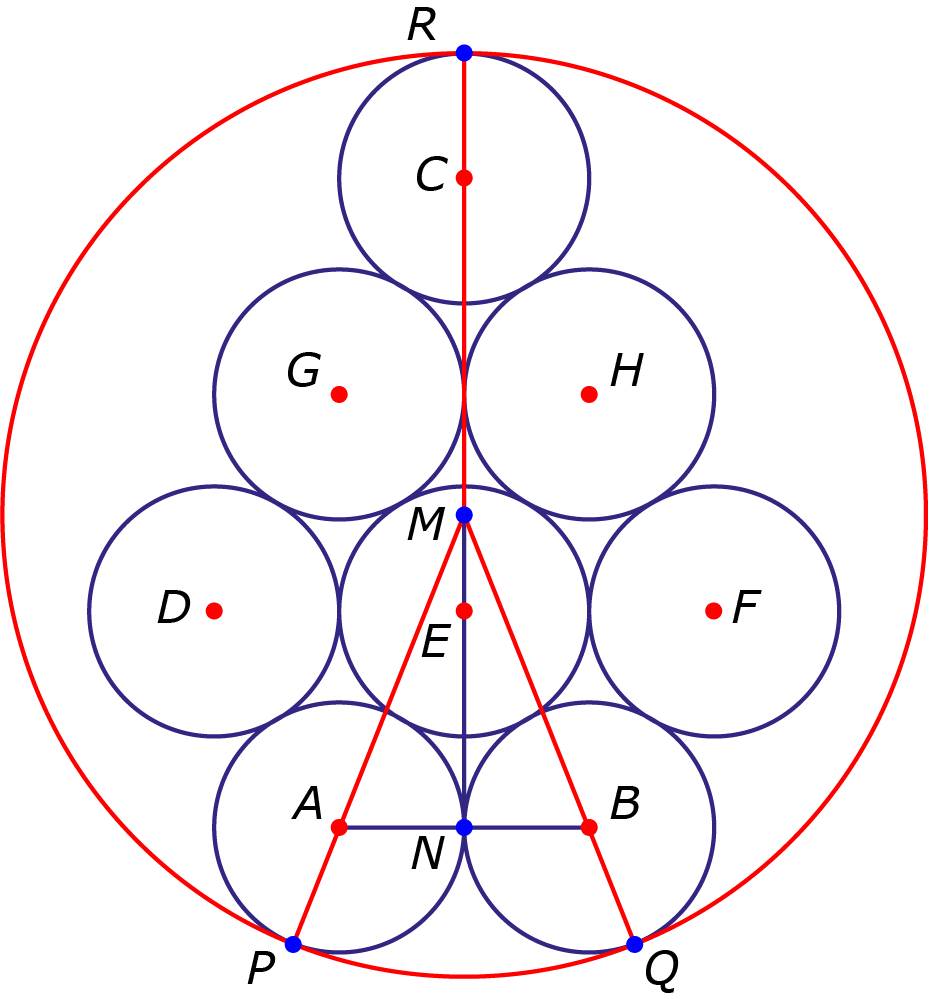

Er is gegeven dat $AN = \sqrt3$. $\triangle ABE$ is gelijkzijdig. Eenvoudig volgt dat $EN = 3$. Zo vinden we dat $CN = 9$. Nu geldt $MN^2 = x^2 - 3$. Tevens geldt $MN = 9 - x$. We vinden uit de vergelijking $(9 - x)^2 - x^2 + 3 = 0$ ofwel $84 - 18x = 0$ dat $x = \frac{14}{3}$. De gevraagde straal is $\frac{14}{3}+\sqrt3.$

 

 

 

 

Opgave 379 [oOO]

Hoeveel factoren $12$ bevat $2018!$ ? En hoeveel factoren $12$ bevat $2025!$ ? Weet dat $n!$ betekent: $1 \times 2 \times 3 \times \cdots \times n$, dus bijvoorbeeld $4! = 1 \times  2 \times  3 \times 4 = 24$.

Oplossing. $12 = 2^2 \times 3$. Steeds met twee factoren $2$ en een factor $3$ heb je een factor $12$. We gaan het aantal factoren $2$ en $3$ in $2018!$ en $2025!$ uitrekenen. Elk even getal bevat (minimaal) een factor $2$. Elk viervoud bevat 2 factoren $2$, elk achtvoud bevat 3 factoren $2$, enzovoort. In formulevorm: het aantal factoren $2$ is $\left\lfloor  \frac{2018}{2} \right\rfloor + \left\lfloor \frac{2018}{2^2} \right\rfloor + \left\lfloor \frac{2018}{2^3} \right\rfloor + \left\lfloor \frac{2018}{2^4} \right\rfloor + \left\lfloor \frac{2018}{2^5} \right\rfloor + \left\lfloor \frac{2018}{2^6} \right\rfloor + \left\lfloor \frac{2018}{2^7} \right\rfloor + \left\lfloor \frac{2018}{2^8} \right\rfloor + \left\lfloor \frac{2018}{2^9} \right\rfloor + \left\lfloor \frac{2018}{2^{10}} \right\rfloor =$ $1009 + 504 + 252 + 126 + 63 + 31 + 15 + 7 + 3 + 1 = 2011.$ (In die formule betekent $\lfloor q \rfloor$ het grootste gehele getal kleiner dan of gelijk aan q.)

Dat zijn 1005 factoren 4. Het aantal factoren 3 is $\left\lfloor \frac{2018}{3} \right\rfloor + \left\lfloor \frac{2018}{3^2} \right\rfloor + \left\lfloor \frac{2018}{3^3} \right\rfloor + \left\lfloor \frac{2018}{3^4} \right\rfloor + \left\lfloor \frac{2018}{3^5} \right\rfloor + \left\lfloor \frac{2018}{3^6} \right\rfloor =$ $672 + 224 + 74 + 24 + 8 + 2 = 1004.$

$2018!$ bevat $1004$ factoren $12$ en geen $1005$ factoren $12,$ want $2018!$ is niet deelbaar door $3^{1005}.$

Voor $2025$ doen we hetzelfde. Het aantal factoren $2$ is $\left\lfloor \frac{2025}{2} \right\rfloor + \left\lfloor \frac{2025}{2^2} \right\rfloor + \left\lfloor \frac{2025}{2^3} \right\rfloor + \left\lfloor \frac{2025}{2^4} \right\rfloor + \left\lfloor \frac{2025}{2^5} \right\rfloor + \left\lfloor \frac{2025}{2^6} \right\rfloor + \left\lfloor \frac{2025}{2^7} \right\rfloor + \left\lfloor \frac{2025}{2^8} \right\rfloor + \left\lfloor \frac{2025}{2^9} \right\rfloor + \left\lfloor \frac{2025}{2^{10}} \right\rfloor =$ $1012 + 506 + 253 + 126 + 63 + 31 + 15 + 7 + 3 + 1 = 2017.$

Dat zijn $1008$ factoren $4$. Het aantal factoren $3$ is $\left\lfloor \frac{2025}{3} \right\rfloor + \left\lfloor \frac{2025}{3^2} \right\rfloor + \left\lfloor \frac{2025}{3^3} \right\rfloor + \left\lfloor \frac{2025}{3^4} \right\rfloor + \left\lfloor \frac{2025}{3^5} \right\rfloor + \left\lfloor \frac{2025}{3^6} \right\rfloor =$ $675 + 225 + 75 + 25 + 8 + 2 = 1010.$

$2025!$ bevat $1008$ factoren $12$ en geen $1009$ factoren $12,$ want $2025!$ is niet deelbaar door $4^{1009}$.

Opgave 380 [oOO]

Bewijs: als in drie van de vier hoekpunten van een viervlak de som van de drie hoeken bij zo’n hoekpunt $180^{\rm o}$ is, dan zijn de vier zijvlakken congruente driehoeken.

Oplossing. De som van de hoeken in een 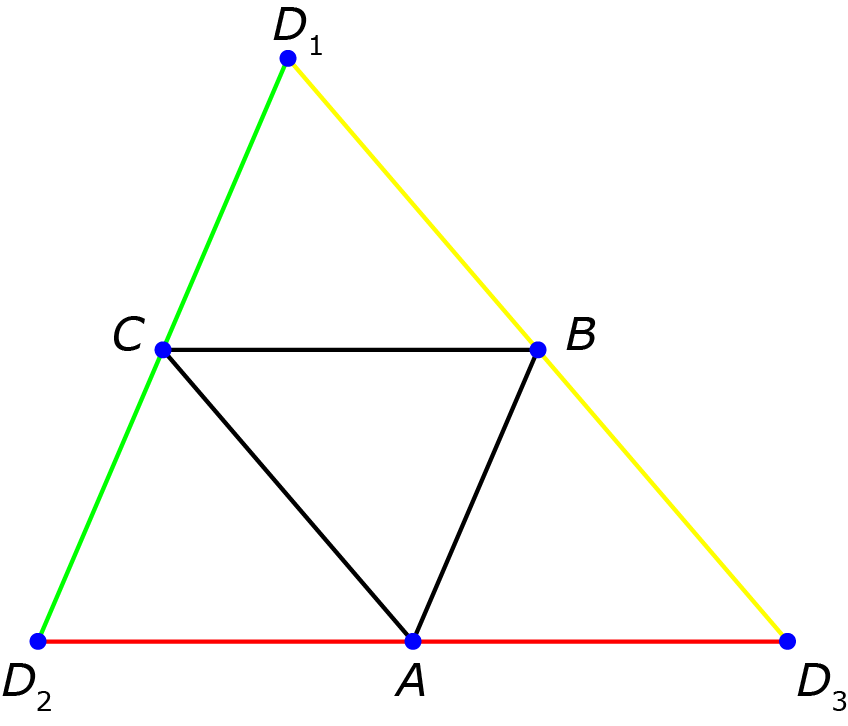driehoek is $180^{\rm o}$ Eenvoudig volgt dat ook voor het vierde hoekpunt moet ook gelden dat de som van de drie hoeken bij dat hoekpunt $180^{\rm o}$ is.

We vouwen de vierhoek uit, vanuit één van de hoekpunten (zeg $D$). Aangezien de som van de hoeken bij elk van de andere hoeken $180^{\rm o}$ is, verkrijgen we een driehoek, waarbij de hoekpunten $A$, $B$ en $C$ de middens zijn van de drie hoekpunten, die we voor het gemak $D_1$, $D_2$ en $D_3$ noemen. Driehoek $\triangle ABD_3$ is gelijkvormig met driehoek $\triangle D_2D_1D_3$, namelijk een factor $2$ kleiner. Dat geldt ook voor $\triangle BD_2CA$ en $\triangle CD_1B$. Ten slotte volgt eenvoudig dat de vier zijvlakken van de viervlak congruent zijn.

Opgave 381 [ooO]

Vind alle gehele getallen $n$ waarvoor geldt:

$$\max(2n - 11 + 2n^6, 2 \max(n - 7 + n^6, 5 - 2n + n^6)) \le 2n^6.$$

Hierbij staat $\max(a, b)$ voor het maximum, dus de grootste, van de getallen $a$ en $b$. Bijvoorbeeld, $\max(3, 5) = 5$, $\max(-3, -5) = -3$ en $\max(3, 3) = 3.$

Oplossing. We maken gebruik van drie rekenregels voor de functie max die eenvoudig te verifiëren zijn: (1) voor $a \ge 0$ geldt $a \max(b, c) = \max(ab, ac)$, (2) voor alle $a$ geldt $a + \max(b, c) = \max(a + b, a + c)$ en (3) $\max(a, \max(b, c)) = \max(\max(a, b), c).$

Om te beginnen halen we een $2$ binnen de $\max$-functie: $2\max(n - 7 + n^6, 5 - 2n + n^6) =$ $ \max(2n - 14 + 2n^6, 10 - 4n + 2n^6).$ Vervolgens trekken we aan beide zijden van de vergelijking $2n^6$ af: $\max(2n - 11, \max(2n - 14, 10 - 4n)) \le 0.$ Volgens de derde rekenregel geldt nu: $\max(\max(2n - 11, 2n - 14), 10 - 4n) \leq 0.$ Aangezien $-11 > -14$ is $\max(2n - 11, 2n - 14) = 2n - 11.$ Er moet gelden $2n - 11 \le 0$ en $10 - 4n \le 0.$ Dan geldt ook dat $\max(2n - 11, 10 - 4n) \le 0.$ Ofwel $n \leq \frac{11}{2}$ en $n \geq \frac{5}{2}.$ De gehele getallen in het interval $\left[\frac{5}{2},\frac{11}{2}\right]$ zijn $\{3, 4, 5\}.$

Opgave 382 [ooO]

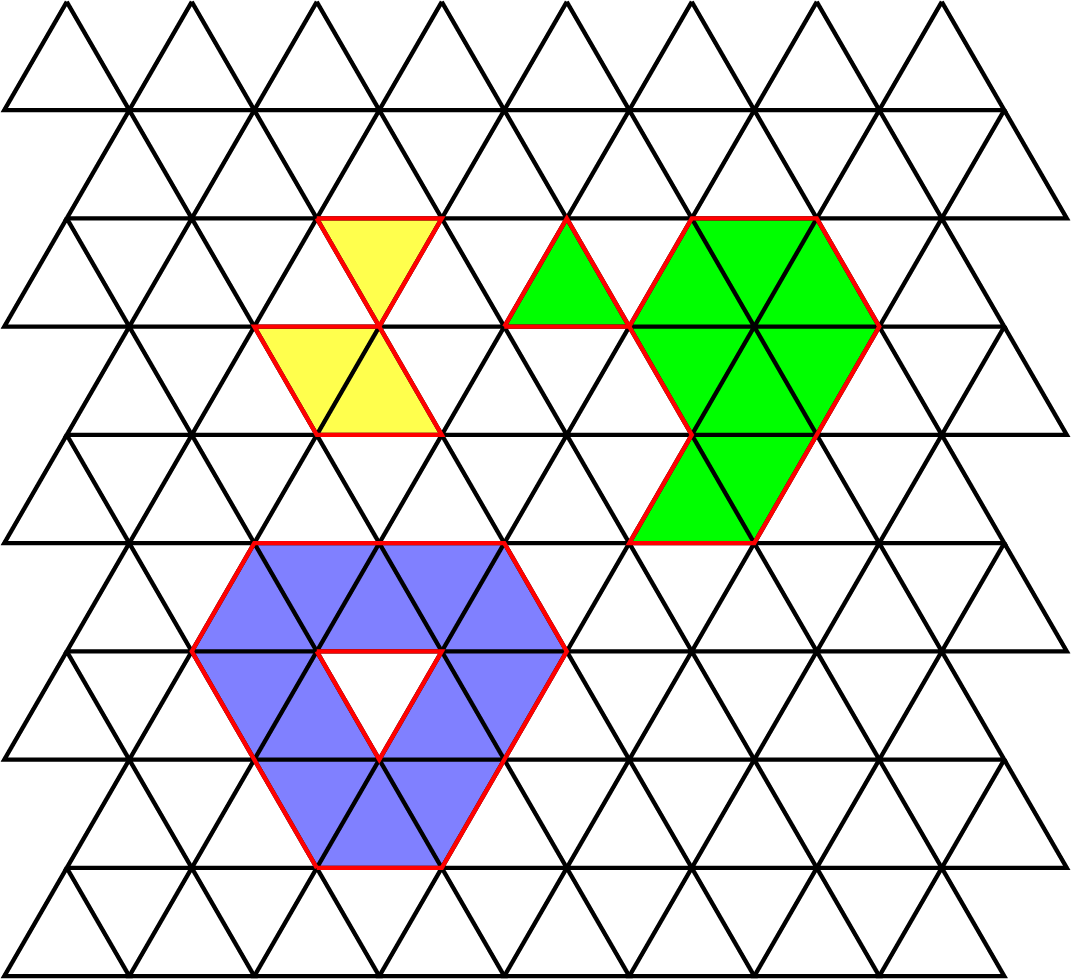Bijgevoegd is een rooster van gelijkzijdige driehoeken. De $12$ blauwe driehoeken hebben een omtrek van lengte $12.$ De $9$ groene driehoeken hebben een omtrek van $11.$ De $3$ gele driehoeken hebben een omtrek van $7.$ We vermoeden dat een even aantal driehoeken altijd een even omtrek heeft en een oneven aantal driehoeken altijd een oneven omtrek heeft. Is dat correct? Bewijs dit of geef een tegenvoorbeeld.

Oplossing. De bewering is inderdaad correct. Het bewijs kan worden geleverd met behulp van volledige inductie. We gaan eerst de situatie bekijken van één driehoek. De omtrek heeft een lengte $3.$ Beiden zijn oneven dus dat is correct. Nu bewijzen we de inductiestap. Dus we hebben alle situaties bestudeerd met $N$ driehoeken en nu bekij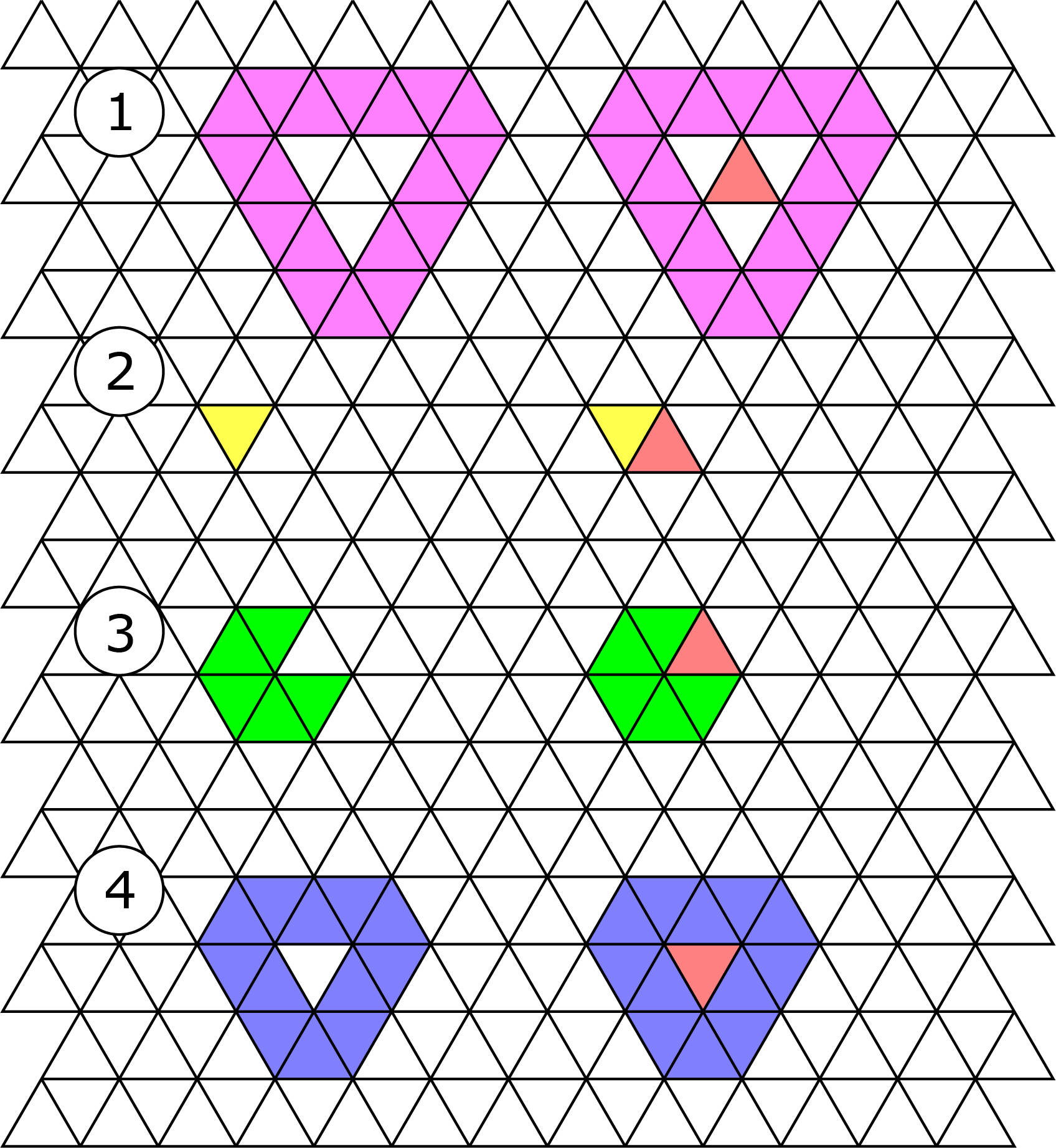ken we een situatie met $N + 1$ driehoeken. Er zijn voor een nieuwe driehoek vier mogelijkheden (zie afbeelding): (1) geen aangrenzende vlakken, (2) één aangrenzend vlak, (3) twee aangrenzende vlakken, en (4) drie aangrenzende vlakken. In de verschillende gevallen bekijken we het verschil van aantal extra randen van de omtrek minus randen die geen deel meer uitmaken van de omtrek. We vinden in de opeenvolgende gevallen  $+3, +2 – 1, +1 – 2$ en $-3$. Dat is steeds oneven.

 

 

 

 

 

 

Opgave 383 [ooO]

Op een atletiekbaan loopt iedereen een deel van een cirkel. Om precies te zijn lopen ze van het rechte blauwe lijnstuk A met de klok mee naar de groene kromme B. Hierbij is de kromme B zo getrokken dat elke deelnemer dezelfde afstand aflegt, waar ze ook beginnen op A. Deze afstand is altijd 400 m. Dit betekent dat het gele stukje tussen A en B nooit gebruikt hoeft te 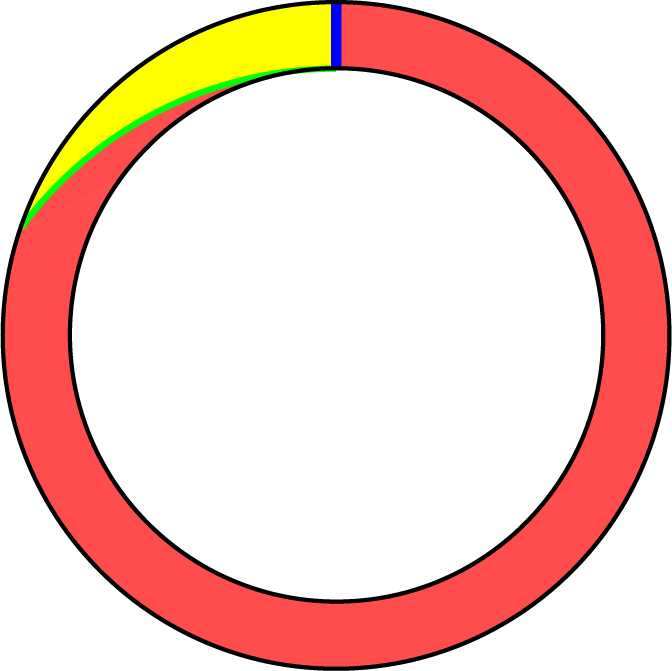worden. Wat is het oppervlak van dit gele gebiedje, als gegeven is dat de buitenste omtrek van de gehele baan 500 m is?

Oplossing:

We bepalen eerst het oppervlak van het deel tussen de twee cirkels. De kleine cirkel heeft een omtrek van $400$ m, daar hoort een straal bij van $\frac{200}{\pi}$ m, en een oppervlak van $\frac{40000}{\pi}$ m². Voor de grote cirkel vinden we een straal van $\frac{250}{\pi}$ m en een oppervlak van $\frac{62500}{\pi}$ m². Het verschil is $\frac{22500}{\pi}$ m². Dat is het oppervlak van het rode en gele gedeelte. Het rode gedeelte heeft overal een breedte van $\frac{50}{\pi}$ (namelijk het verschil van de twee stralen) en de lengte is overal constant, namelijk 400 m. Deze oppervlakte is $\frac{20000}{\pi}$ m². De oppervlakte van het gele gedeelte is dus $\frac{22500}{\pi}$ m² $ - \frac{20000}{\pi}$ m² = $\frac{2500}{\pi}$ m².

Opgave 384 [ooo]

Goed voor drie punten!

We hebben $D(n)$, de som van de cijfers van een natuurlijk getal $n$, en $R(n),$ het omgekeerde van $n.$

Bijvoorbeeld: $D(271) = 2 + 7 + 1 = 10$ en $R(271) = 172$. Bepaal alle natuurlijke getallen $n$ met $D(n) \times R(D(n)) = n.$

Oplossing. We introduceren vooraf $c(n)$, het aantal cijfers van $n$, ofwel in formule $c(n) = \lfloor^{10}\log(n)\rfloor$, waarbij de functie $\lfloor q\rfloor$ het grootste gehele getal kleiner dan of gelijk aan $q$ geeft. Er geldt $^{10}\!\log(n) - 1 < c(n) \le {}^{10}\!\log(n).$

We bekijken twee gevallen: $n < 10000$ en $n \ge 10000.$ We bekijken eerst het laatste geval. We schatten eerst $D(n)$ af: $D(n) \le 9c(n)$, en ook $R(D(n)) \le 9c(n)$, zodat $n = D(n) \times R(D(n)) \le 81(c(n))^2 < 100(^{10}\log(n))^2 < n$. Deze allerlaatste ongelijkheid volgt uit $^{10}\!\log(n) < \frac1{10}\sqrt{n}$, voor $n > 10000$, en kan zelf worden geverifiëerd.

Nu weten we dat $n < 10000$. We noemen $k = D(n)$. In plaats van te kijken naar oplossingen $n$ waarvoor geldt dat $D(n) \times R(D(n)) = n$, kijken we naar $k$ waarvoor geldt dat enerzijds het product $n = k \times R(k)$, en anderzijds $D(n) = k$. Als $n < 10000$ dan geldt $k \le 36$. We hoeven nog maar $36$ waarden voor $k$ te checken. Maar we kunnen nog een reductie uitvoeren.

We gaan nu kijken welke getallen modulo $9$ in aanmerking komen (ofwel we bekijken de getallen waarvan we een negenvoud aftrekken, zodat er een getal tussen $0$ en $8$ overblijft). Er geldt dat $n - D(n)$ is een negenvoud, maar ook $D(n) - R(D(n))$ is een negenvoud. We bekijken de tabel voor $n$ en $n^2$, waarbij we zoveel mogelijk veelvouden van $9$ aftrekken zodat er getallen tussen $0$ en $8$ overblijven.

$n \mod 9$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$
$n^2 \mod 9$	$0$	$1$	$4$	$0$	$7$	$7$	$0$	$4$	$1$

Alleen veelvouden van $9$ en veelvouden van $9$ plus $1$ blijven over. We hoeven alleen nog $k \in \{1, 9, 10, 18, 19, 27, 28, 36\}$ te controleren.

Uiteindelijk vinden we oplossingen voor $k \in \{1, 9, 18, 19\}$. De bijbehorende waarden van $n$ zijn $1, 81, 1458$ en $1729$.