Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 31 oktober 2018.

Opgave 385 [niveau oOO]

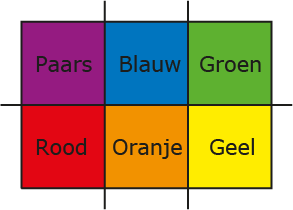
Je hebt een rechthoek van $2 \times 3$ vierkanten. Elk vierkant heeft een eigen kleur, onder en boven. Door drie keer naar keuze te vouwen volgens de scheidslijnen (die iets langer zijn getekend) krijg je een stapeltje van de zes vierkantjes op elkaar. Hoeveel verschillende kleurenvolgordes zijn er met rood aan een einde?

Opgave 386 [niveau oOO]

Jan en Piet nippen ieder een glas cola van $200 ml$. Jan drinkt iedere $2$ minuten $20 ml$ en Piet iedere $2$ minuten $10 ml$. Jan is hebberig, en kijkt daarom om de $2$ minuten wie er nog het meeste over heeft. Als dit Piet is, dan wisselt hij stiekem de glazen om. Dit wisselen kost geen tijd. Hoe lang duurt het voor er voor het eerst een glas op is?

Opgave 387 [niveau ooO]

Vind alle gehele getallen $n$ waarvoor geldt: $\max(2n – 11 + 2n^6, 2 \max(n – 7 + n^6, 5 – 2n + 6n^6)) ≤ 2n^6$.
Hierbij staat $\max(a, b)$ voor het maximum, dus de grootste, van de getallen $a$ en $b$. Bijvoorbeeld, $\max(3, 5) = 5$, $\max(-3, -5) = -3$ en $\max(3, 3) = 3$.

Opgave 388 [niveau ooO]

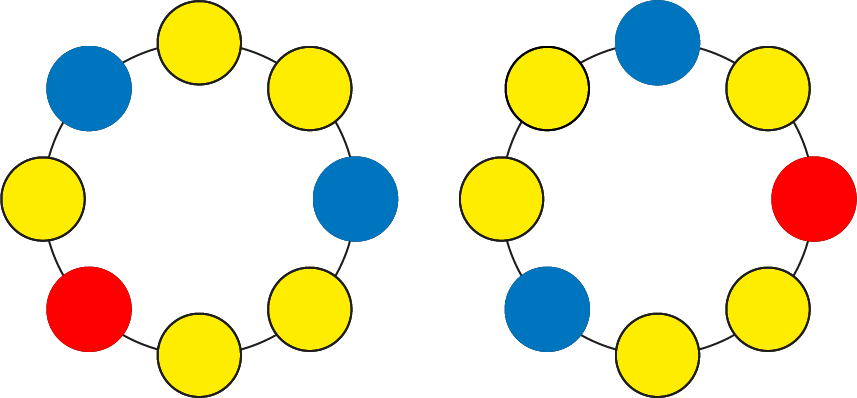
Marieke heeft $8$ kralen: één rode kraal, twee blauwe kralen en voor de rest gele kralen. Ze rijgt daarmee een ketting. Hoeveel verschillende kettingen kan ze zo rijgen? Let op: twee kettingen die elkaars gespiegelde zijn, of die ten opzichte van elkaar iets zijn gedraaid tellen als één ketting. Hieronder is één ketting tweemaal afgebeeld.

 

Bekijk oplossing