Opgave 385 [niveau oOO]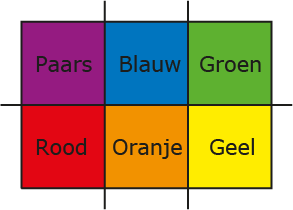

Je hebt een rechthoek van $2 \times 3$ vierkanten. Elk vierkant heeft een eigen kleur, onder en boven. Door drie keer naar keuze te vouwen volgens de scheidslijnen (die iets langer zijn getekend) krijg je een stapeltje van de zes vierkantjes op elkaar. Hoeveel verschillende kleurenvolgordes zijn er met rood aan een einde?

 

 

 

Oplossing. In de oplossing zorgen we dat het vel papier zo wordt gevouwen dat rood bovenop terechtkomt. Zoals in de opgave staat zijn er drie vouwlijnen. Voor de eerste vouw maakt het niets uit of er naar boven of naar beneden wordt gevouwen. We veronderstellen dat we zo vouwen dat rood bovenop komt te liggen. Bij de tweede (en derde vouw) maakt het wel uit hoe er wordt gevouwen.  Van belang is dat na de vouw rood nog steeds bovenop terechtkomt.

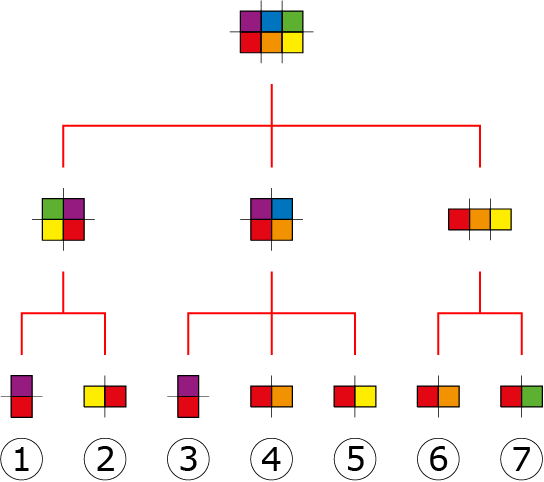
Hiernaast is een grafische weergave:

 

 

Uiteindelijk vinden we de volgende 7 oplossingen:

1	Rood, paars, blauw, oranje, geel, groen
2	Rood, paars, geel, groen, blauw, oranje
3	Rood, paars, blauw, groen, geel, oranje
4	Rood, paars, groen, blauw, oranje, geel
5	Rood, geel, oranje, blauw, groen, paars
6	Rood, oranje, geel, groen, blauw, paars
7	Rood, oranje, blauw, paars, groen, geel
-------
8	Rood, oranje, blauw, groen, geel, paars
9	Rood, groen, geel, oranje, blauw, paars

De laatste twee oplossingen worden niet goedgekeurd, omdat hier niet alleen gebruik is gemaakt van vouwen, maar ook van het buigen van het papier.

Opgave 386 [niveau oOO]

Jan en Piet nippen ieder een glas cola van $200\mbox{ ml}.$ Jan drinkt iedere $2$ minuten $20\mbox{ ml}$ en Piet iedere $2$ minuten $10\mbox{ ml}.$ Jan is hebberig, en kijkt daarom om de $2$ minuten wie er nog het meeste over heeft. Als dit Piet is dan wisselt hij stiekem de glazen om. Dit wisselen kost geen tijd. Hoe lang duurt het voor er voor het eerst een glas op is?

Oplossing. Stel dat Jan en Piet op een gegeven moment evenveel cola hebben, zeg $x\mbox{ ml}.$ Dan heeft Jan na $2$ minuten nog $x - 20\mbox{ ml}$ en Piet nog $x - 10\mbox{ ml}.$ Aangezien Jan nu minder heeft, zal hij de glazen nu omwisselen. Jan heeft nu dus $x - 10\mbox{ ml}$ en Piet $x - 20\mbox{ ml}.$ Na nog eens $2$ minuten staan ze beide op $x - 30\mbox{ ml}.$ Dit betekent dat ze steeds na $4$ minuten weer gelijk staan, en dat er uit elk glas dan $30\mbox{ ml}$ is gedronken. Na $24$ minuten hebben ze dus ieder nog $200 - 180 = 20\mbox{ ml}$ over. $2$ minuten later drink Jan zijn glas leeg, en is er dus voor het eerst een glas op. In totaal duurt dit daarom $26$ minuten.

OPGAVE 387 [niveau ooO]

Vind alle gehele getallen $n$ waarvoor geldt:

$$\max(2n - 11 + 2n^6, 2\max(n - 7 + n^6, 5 - 2n + \mathbf{6}n^6)) \le 2n^6.$$

Hierbij staat $\max(a, b)$ voor het maximum, dus het grootste, van de getallen $a$ en $b$. Bijvoorbeeld, $\max(3, 5) = 5$, $\max(-3, -5) = -3$ en $\max(3, 3) = 3.$

Oplossing: De opgave is door de toegevoegde 6 (vetgedrukt) toch anders dan opgave 381 in Pythagoras 57-5/6.

We maken gebruik van drie rekenregels voor de functie max die eenvoudig te verifiëren zijn:

1. voor $a \leq 0$ geldt $a \max(b,c) = \max(ab,ac)$,
2. voor alle $a$ geldt $a+ \max(b,c) = \max(a+b,a+c)$ en
3. $\max(a, \max(b,c)) = \max(\max(a,b),c) = \max(a,b,c)$.

Het linkerlid kunnen we herschrijven tot $\max(2n-11+2n^6,2n-14+2n^6,10-4n+12n^6)$. Merk op dat $2n-11+2n^6 > 2n-14+2n^6$. Zodoende reduceert de ongelijkheid tot $\max(2n-11+2n^6,10-4n+12n^6) \leq 2n^6$. Vervolgens trekken we aan beide zijden van de ongelijkheid $2n^6$ af. We hebben nu  $\max(2n-11,10-4n+10n^6) \leq 0$. Nu geldt echter dat $10-4n+10n^6$ uitsluitend positieve waarden heeft. Immers we kunnen de functie $f(x) = 10-4n+10n^6$ onderzoeken. Zowel als $x$ naar $+\infty$ als naar $-\infty$ gaat gaat de functiewaarde naar $\infty$. Vervolgens bepalen we het minimum door de afgeleide te bepalen: $f'(x) = -4+60x^5$. Als de afgeleide 0 is neemt de functie het minimum aan. Dit is voor $x = \sqrt[5]{\frac{1}{15}}$. De bijbehorende functiewaarde is $f\left(\sqrt[5]{\frac{1}{15}}\right) \approx 8,06$. Er zijn geen oplossingen.

OPGAVE 388 [niveau ooO]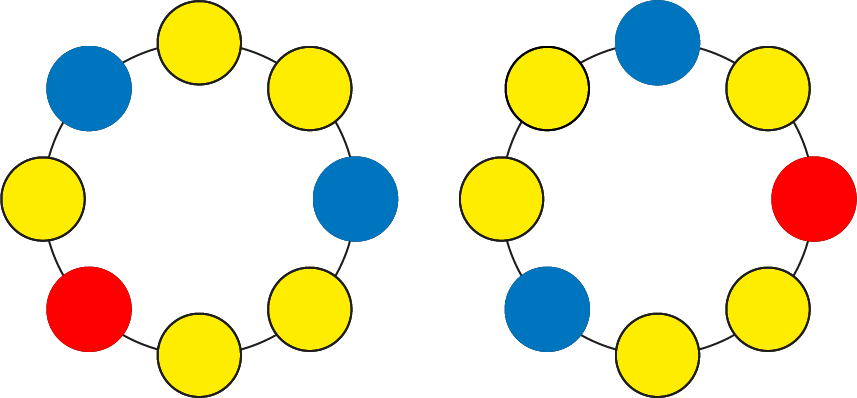

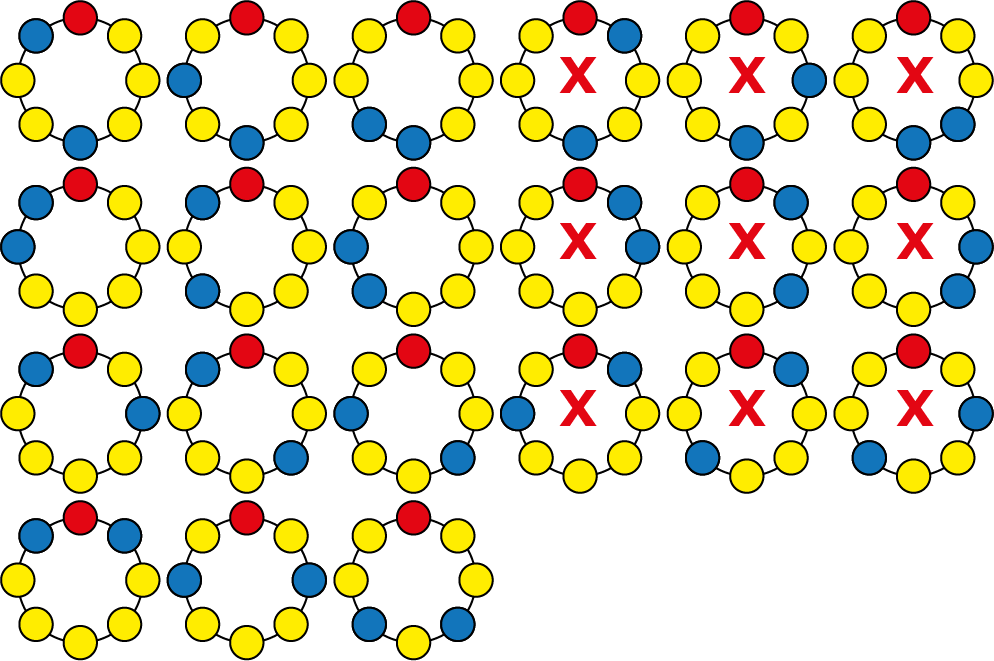
Marieke heeft 8 kralen: één rode kraal, twee blauwe kralen en voor de rest gele kralen. Ze rijgt daarmee een ketting. Hoeveel verschillende kettingen kan ze zo rijgen? Let op: twee kettingen die elkaars gespiegelde zijn, of die ten opzichte van elkaar iets zijn gedraaid tellen als één ketting. Hiernaast is één ketting tweemaal afgebeeld.

Oplossing. Als je eenmaal een ketting hebt geregen en je verdraait de ketting één kraal dan heb je nog steeds dezelfde ketting. We draaien de ketting totdat de rode kraal bovenaan zit. Doen we dat voor de twee kettingen die als voorbeeld zijn afgebeeld, dan krijg je twee kettingen die het spiegelbeeld zijn van elkaar. We onderscheiden om te beginnen een aantal locaties van de kralen: (1) de kraal beneden (2) de kralen links en (3) de kralen rechts. Op grond van deze locaties kunnen de volgende mogelijkheden voorkomen:

1. [3] blauwe kralen beneden en links;
2. [3] blauwe kralen beneden en rechts;
3. [3] blauwe kralen beide links;
4. [3] blauwe kralen beide rechts;
5. [3] één blauwe kraal links één rechts op gelijke hoogte;
6. [6] één blauwe kraal links één rechts op ongelijke hoogte.

In de rechthoekige haken is het aantal mogelijkheden geplaatst. Het totaal hiervan is $21,4 maar dat is niet het aantal verschillende kettingen. Er worden namelijk kettingen dubbel geteld.

De mogelijkheden van 1. en 2. zijn steeds gespiegeld aan elkaar. Dat geldt ook voor de mogelijkheden van 3. en 4.

De mogelijkheden bij 6. worden dubbel geteld, want voor het spiegelbeeld geldt eveneens dat zich één blauwe kraal links één rechts op ongelijke hoogte bevinden. We moeten het totale aantal verminderen met $9.$ Het antwoord is $12.$

Ook door het uittekenen van de oplossingen kom je tot de oplossing.