Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 31 december 2018.

Opgave 389 [niveau oOO]

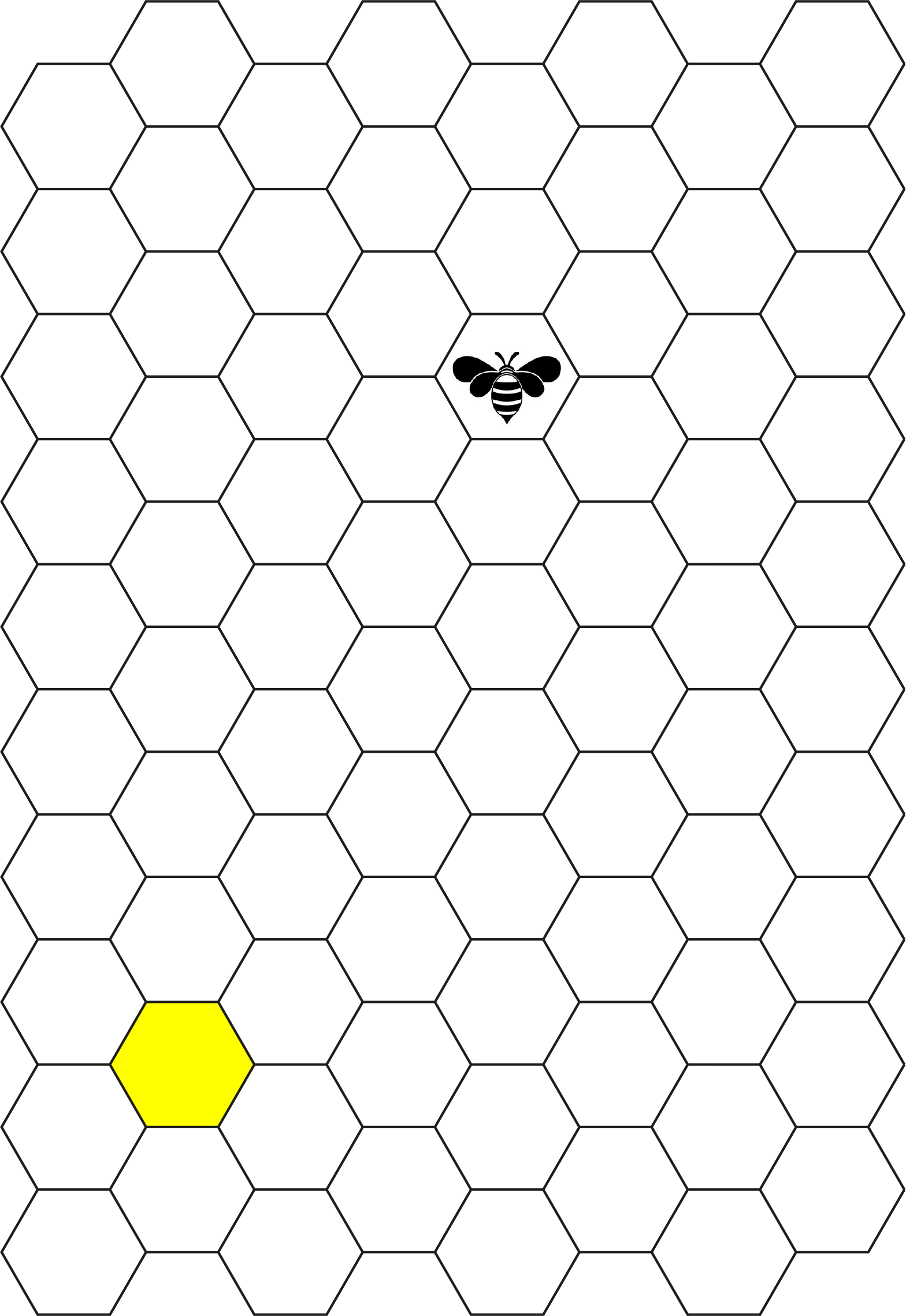
Een bij zit op een cel van een bijenraat en ziet verderop een cel gevuld met honing (geel gekleurd). De bij steekt steeds een celwand over van de ene naar de andere cel. Hoe lang is de kortste route en op hoeveel manier kan de bij naar de honingcel wandelen?

 

 

 

 

 

 

Opgave 390 [niveau oOO]

Gegeven is de onderstaande driehoek met zijden 11, 13 en 20. Het lijnstuk met lengte 15, neergelaten vanuit de tophoek, deelt de basis in twee lijnstukken met lengten p en q. Bepaal p en q.

Opgave 391 [niveau ooO]

Toon aan dat de volgende som kleiner is dan 1:

$$\left(\sqrt2-1\right) + \left(\sqrt{\sqrt2}-1\right) + \left(\sqrt{\sqrt{\sqrt2}} -1\right) + \dots.$$

Elke volgende term bevat een extra wortelteken.

Opgave 392 [niveau 2 ooO]

Alfred en Samira maken een afspraakje om Beatrice te imponeren. Ze doen het volgende spelletje met 6 kaarten. Deze liggen blind op tafel met de cijfers 1 tot en met 6 op de onderkanten. Beatrice mag er 3 willekeurig uitkiezen en blind terzijde schuiven. Alfred pakt de andere 3 op en bekijkt ze. Dan geeft hij er 1 van aan Samira. Ze bekijkt deze en zegt: "Je hebt zeker die en die kaart ook in handen, Alfred." Dat zegt ze altijd goed, hoe vaak ze het spelletje ook doen. Beatrice snapt er eerst niets van, maar later begrijpt ze wat Samira en Alfred hebben afgesproken. Weet jij ook wat Alfred en Samira hebben afgesproken?

Bekijk oplossing