Opgave 389 [niveau oOO]

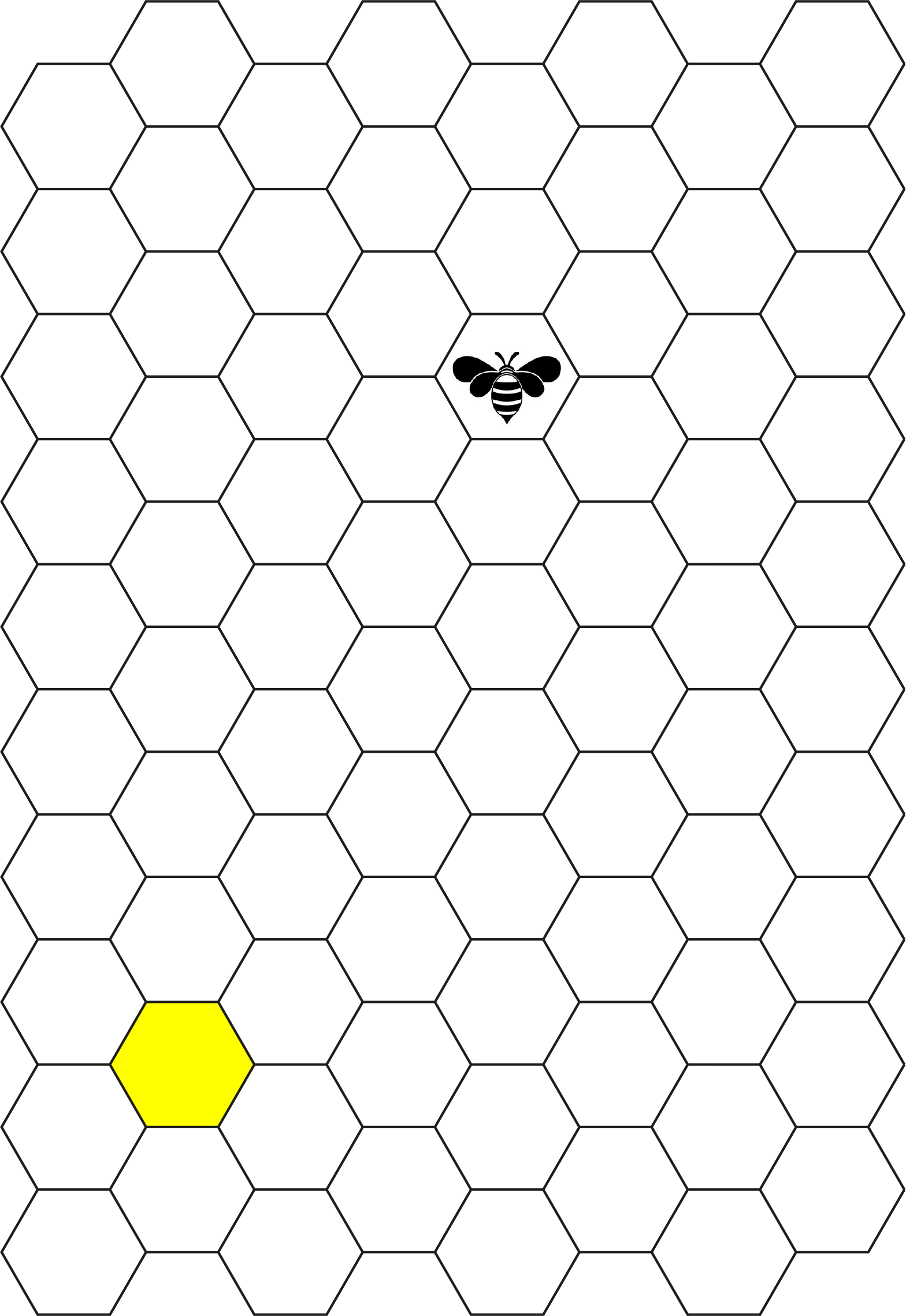Een bij zit op een cel van een bijenraat en ziet verderop een cel gevuld met honing (geel gekleurd). De bij steekt steeds een celwand over van de ene naar de andere cel. Hoe lang is de kortste route en op hoeveel manieren kan de bij naar de honingcel wandelen volgens zo’n kortste route?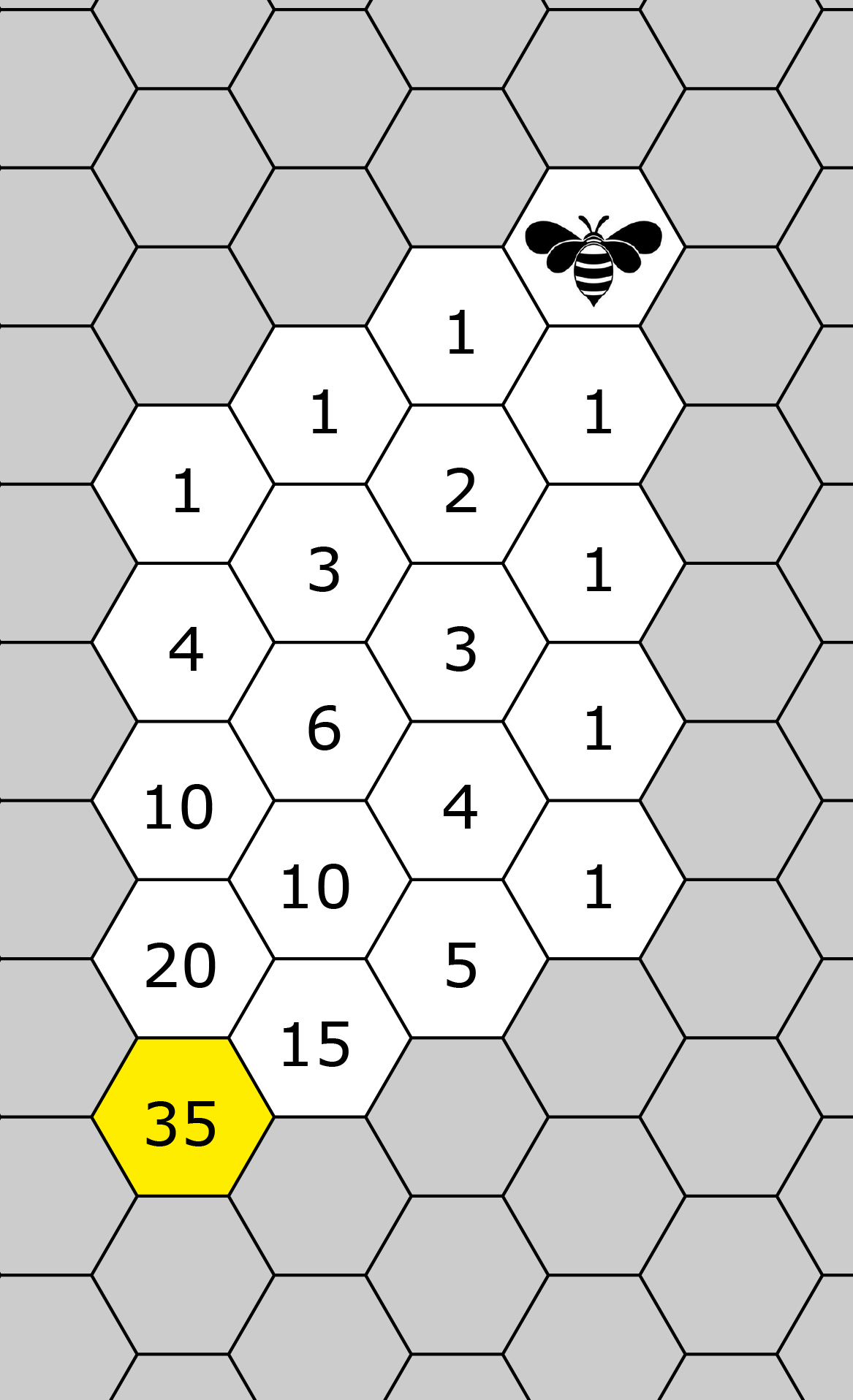

Oplossing. We laten de bij lopen in de richting van de cel met de honing. In het plaatje hieronder is te zien hoeveel mogelijkheden de bij heeft vanaf het beginpunt tot aan de betreffende cel. Voor aangrenzende cellen is dat $1.$ Dan is er een cel die de bij op twee manieren kan bereiken, namelijk bovenlangs en via de rechterzijde. Het aantal mogelijkheden neemt toe: steeds moet je de aantallen mogelijkheden van de cellen rechts en boven bij elkaar optellen. Zo vinden we als antwoord $35.$

Een alternatieve oplossing (meer voor de bovenbouw) maakt gebruik van het aantal combinaties. De bij moet $7$ stappen doen, waarvan $3$ naar links en $4$ naar beneden. De vraag is hoeveel volgordes er zijn van links en naar beneden. Dat aantal is ${7\choose 3} = 35$

Opgave 390 [niveau oOO]

Gegeven is de nevenstaande driehoek met zijden $11, 13$ en $20.$ Het lijnstuk met lengte $15,$ neergelaten vanuit de tophoek, deelt de basis in twee lijnstukken met lengten $p$ en $q.$ Bepaal $p$ en $q.$

Oplossing. Uitgaande van de driehoek $\triangle ABD$ tekenen de loodlijn $BC.$ De afstand $BC$ noemen we $h$ en de afstand $BC$ noemen we $r.$ Nu geldt $h^2 + r^2 = 13^2 = 169,$ $h^2 + (q + r)^2 = 15^2 = 225$ en $h^2 + (r + 11)^2 = 20^2 = 400.$ Door combineren van de eerste en laatste vergelijking vinden we $(r + 11)^2 - r^2 = 231.$ Na het wegwerken van de haakjes vinden we $22r + 121 = 231$ ofwel $r = 5.$ Eenvoudig volgt $h = 12.$ Substitueren we deze waarden in de tweede vergelijking dan vinden we $q = 4$ en $p = 7.$

Opgave 391 [niveau ooO]

Toon aan dat de volgende som kleiner is dan $1{:}$

$\left(\sqrt{2}-1\right) + \left(\sqrt{\sqrt{2}}-1\right) + \left(\sqrt{\sqrt{\sqrt{2}}} -1\right) + \dots.$

Elke volgende term bevat een extra wortelteken.

Oplossing. We noteren $a_n = \underbrace{\sqrt{\sqrt{\dots\sqrt{2}}}}_{n\ {\rm wortels}}$ en $b_n = a_n - 1.$

We zien direct dat $b_1 = \sqrt2 - 1 < \frac12$. Er geldt $a_{n+1}^2 = a_n$ ofwel $(b_{n+1} + 1)^2 = b_{n+1}$ ofwel $2b_{n+1} + b_{n+1}^2 = b_n.$ We concluderen $2b_{n+1}< b_n.$ Met behulp van inductie vinden we $b_{n} < \frac1{2^n}$. Voor de gevraagde som geldt $b_1+b_2+b_3+\dots+b_n+\dots < \frac12 + \frac14 + \frac18 + \dots + \frac1{2^n} + \dots = 1$.

Opgave 392 [niveau ooO]

Alfred en Samira maken een afspraakje om Beatrice te imponeren. Ze doen het volgende spelletje met $6$ kaarten. Deze liggen blind op tafel met de cijfers $1$ tot en met $6$ op de onderkanten. Beatrice mag er $3$ willekeurig uitkiezen en blind terzijde schuiven. Alfred pakt de andere $3$ op en bekijkt ze. Dan geeft hij er $1$ van aan Samira. Ze bekijkt deze en zegt: "Je hebt zeker die en die kaart ook in handen, Alfred." Dat zegt ze altijd goed, hoe vaak ze het spelletje ook doen. Beatrice snapt er eerst niets van, maar later begrijpt ze wat Samira en Alfred hebben afgesproken. Weet jij ook wat Alfred en Samira hebben afgesproken?

Opmerking. Bij het nakijken van de inzendingen bleek dat een aantal inzenders op zoek was gegaan naar een unieke oplossing. De oplossing is echter niet uniek. Vandaar dat de opgave nog even open blijft staan en iedereen in de gelegenheid wordt gesteld om een zo bondig mogelijke oplossing in te sturen.