Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 15 juli 2019.

Opgave 401 [oOO]

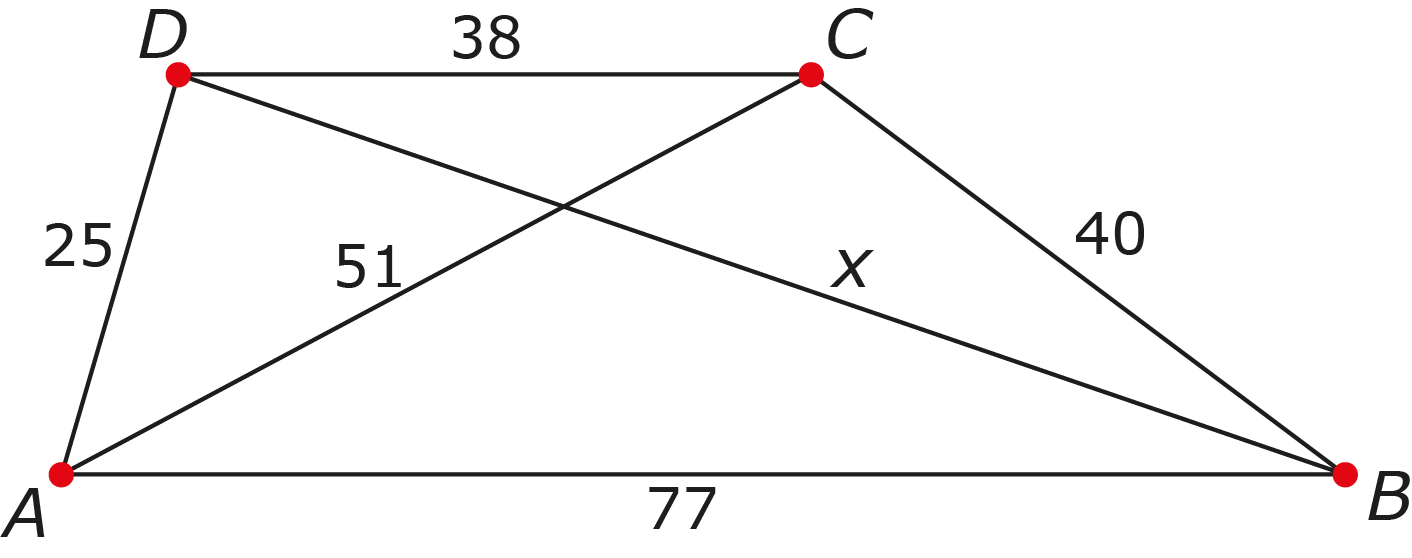
Gegeven trapezium $ABCD,$ waarbij $AB$ evenwijdig is aan $CD.$ Bovendien zijn de volgende lengten gegeven: $AB = 77, BC = 40, CD = 38, AD = 25$ en $AC = 51.$ Bepaal de lengte van de andere diagonaal $BD.$

Opgave 402 [oOO]

We hebben het volgende schuifspelletje: in elk vakje van de strook komt een getal. Er zijn reeds twee getallen ingevuld. De som van de drie getallen uit de drie linkse vakken is $14.$

Telkens als het raam (rood) één vakje naar rechts schuift vermeerdert de som van de drie getallen binnen het venster met $1.$ Bepaal de 10 getallen op het strookje.

Opgave 403 [ooO]

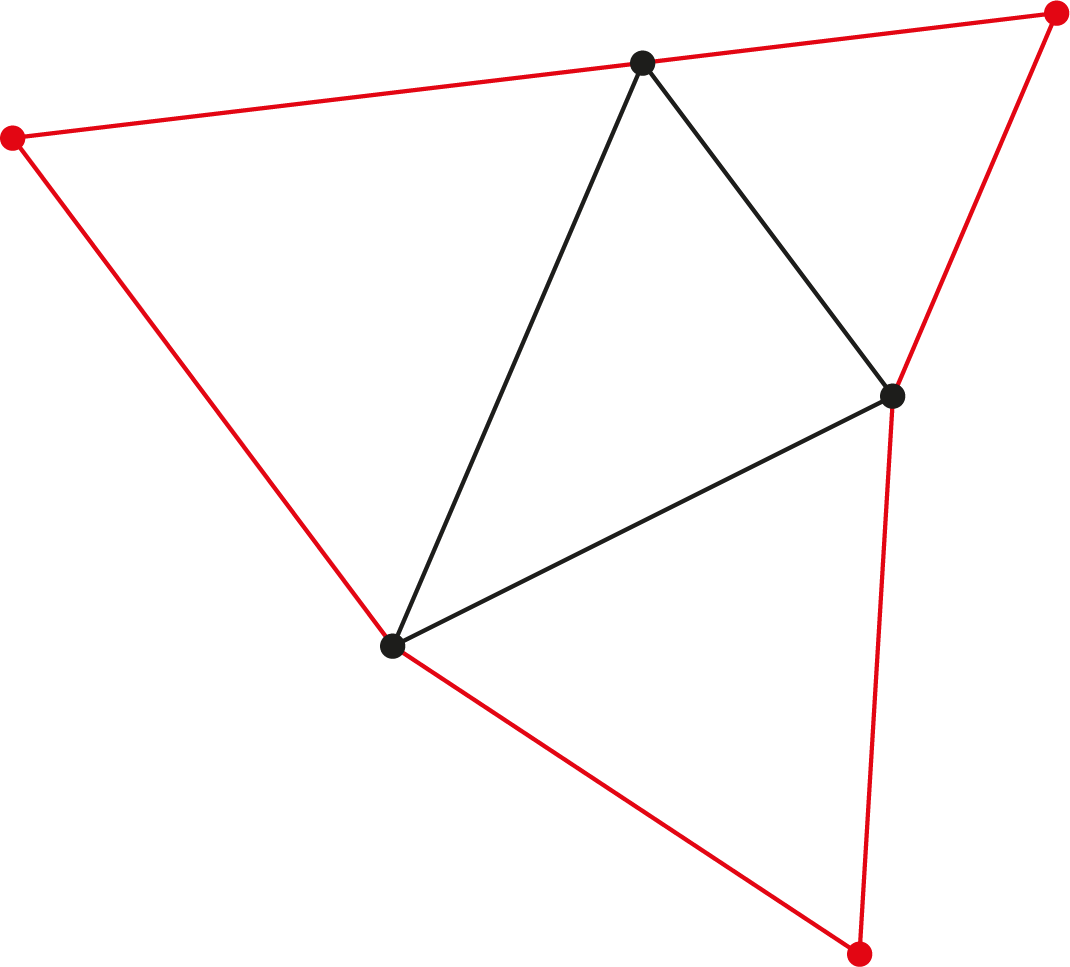
We gaan uit van een willekeurige driehoek. We construeren vervolgens drie punten buiten de driehoek, door op elke zijde een gelijkzijdige driehoek te plaatsen. In de figuur hieronder is een voorbeeld geplaatst.

Het is mogelijk om uitgaande van deze drie punten weer de oorspronkelijke driehoek construeren (met passer en liniaal). Hoe ziet de constructie er uit? Hint: maak gebruik van het punt van Torricelli (zie achterop dit nummer).

Opgave 404 [ooO]

We beschouwen een dambord (afmetingen $10 \times 10).$ Verder hebben we een heel bijzonder schaakstuk; een (2, 3)-paard werkt net zoals een gewoon paard, behalve dat het steeds sprongen van 2 hokjes opzij en 3 naar boven of onderen, of 3 opzij en 2 naar boven of onderen maakt. We plaatsen een (2, 3)-paard ergens in dit dambord. Is het voor zo’n paard mogelijk om één vakje opzij te bereiken (rechts of links)? Waarom wel of niet?

Bekijk oplossing