Opgave 401 [oOO]

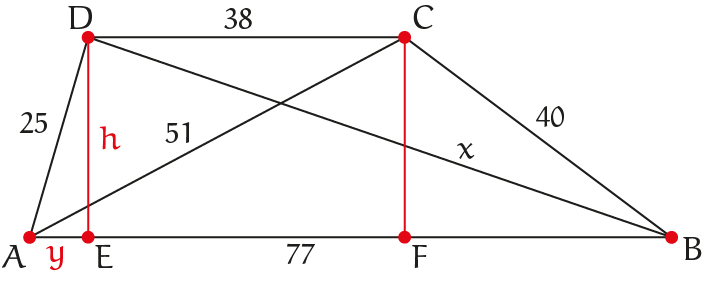Laat $E$ de loodrechte projectie van $D$ en $F$ die van $C$ op $AB$ zijn. We stellen de lengte van $AE$ gelijk aan $y$ en van $DE$ en $CF$ gelijk aan h. $EF = 38$ en $FB = 77 -$ y. Uit de stelling van Pythagoras op $\Delta AED$ volgt $h^2 + y^2 = 25^2 = 625$ en uit de stelling van Pythagoras op $\Delta FBC$ volgt $h^2 + (39 - y)^2 = 40^2 = 1600$. Het verschil van deze vergelijkingen geeft $1521 - 78y = 975$ en dus $y = 7$. Hieruit volgt dat $h = 24$. De stelling van Pythagoras toepassen op $\Delta EBD$ levert $70^2 + 24^2 = x^2$ en dus $x = 74$.

Opgave 402 [oOO]

Geef de openstaande vakjes de waarden $x_1, x_3, x_4, \ldots , x_9$.

Er geldt dat $x_1 + 8 + x_3 = 14$ en $8 + x_3 + x_4 = 15$, dus $x_4 = x_1 + 1$. Op vergelijkbare wijze krijg je $x_{i+3} = x_i + 1$ en dus $4 = x_7 + 1$. Hieruit kun je de resterende getallen eenvoudig berekenen en je krijgt als eindresultaat:

Opgave 403 [ooO]

We plaatsen hier een oplossing die gebaseerd is op de inzending van Marijn Adriaanse. In de constructie van de driehoek $\Delta ABC$ hebben we het volgende nodig: gegeven twee gelijkzijdige driehoeken $\Delta PQR$ en $\Delta P_1QR_1$, zoals hiernaast getekend, dan geldt $|PQ| = |PP_1| + |PR_1|$.

Bewijs. We bekijken de driehoeken $\Delta PQP_1$ en $ \Delta RQR_1$. Er geldt $|QR| = |QP|, |QR_1| = |QP_1| $ en de hoeken $\angle RQR_1$ en $\angle PQP_1$ zijn gelijk. Dan volgt $|PP_1| = |RR_1|$. Nu volgt $|PQ| = |PR| = |PR_1| + |R_1R| = |PP_1| + |PR_1|$.
Q.E.D.

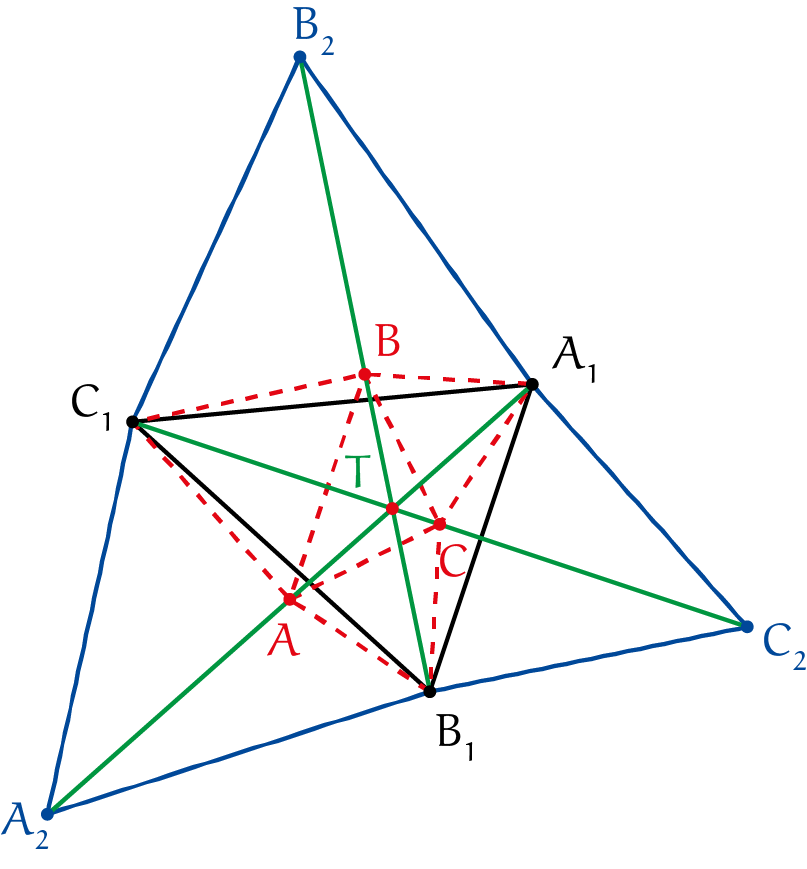
Opmerking. Uiteindelijk passen we dit toe zonder daadwerkelijk het punt $R$ te gebruiken. Van belang is dat $P_1QR_1$ een gelijkzijdige driehoek is en de hoeken $\angle QPR = 60^{\rm o}$ en $ \angle P_1PQ = 60^{\rm o}$ zijn. We hebben in geel de oorspronkelijke driehoek nog getekend. Driehoek $\Delta A_1B_1C_1$ is de driehoek van de extra getekende drie hoekhoekpunten van de drie gelijkzijdige driehoeken. We bepalen eerst het punt van Torricelli van deze driehoek. Volgens de achterkant van Pythagoras 58-5 (april 2019) moet je op alle drie de zijden een gelijkzijdige driehoek plaatsen. De drie nieuwe hoekpunten zijn $A_2 $ (op de zijde $B_1C_1), B_2$ (op de zijde $A_1C_1)$ en $ C_2$ (op de zijde $A_1B_1)$. Het snijpunt van $A_1A_2 $ en $B_1B_2$ is het punt van Torricelli, hetgeen we weergeven met $T. $ We bepalen eerst het punt van Torricelli van de oorspronkelijke driehoek $\Delta ABC$. Dit punt van Torricelli valt samen met het punt van Torricelli van de driehoek $\Delta A_1B_1C_1, $ immers de punten $A, B$ en $C$ liggen tegenover de punten $A_1, B_1$ en $C_1$, zodoende zijn de hoeken die de lijnstukken $AT, BT$ en $CT $ onderling maken steeds $120^{\rm o}$, per defi nitie dus het punt van Torricelli. Bewering: $A$ ligt in het midden van lijnstuk $A_1A_2, B$ ligt in het midden van lijnstuk $B_1B_2$ en $C$ ligt in het midden van lijnstuk $ C_1C_2. $ We tonen deze bewering aan: ten eerste laten we zien dat $|BT| + |CT| = |A_1T|$. Dit volgt direct uit het feit dat $\Delta A_1BC$ een gelijkzijdige driehoek is, en $\angle A_1TB = \angle A_1TC = 60^{\rm o}$. Evenzo vinden we $|AT| + |CT| = |B_1T| $ en $|AT| + |BT| = |C_1T|$. Maar ook kunnen we nagaan dat geldt dat $|B_1T| + |C_1T| = |A_2T|$ (op vergelijkbare wijze). We vinden door substitutie van $|B_1T|$ en $|C_1T|$ dat $|A_2T| = |B_1T| + |C_1T| = 2|AT| + |BT| + |CT| = 2|AT| + |A_1T|$. Nu geldt $|A_1A_2| = |A_2T| + |A_1T| = 2(|AT| + |A_1T|) = 2|AA_1|. $ Daarmee kan de oorspronkelijke driehoek $\Delta ABC$ eenvoudig worden geconstrueerd.

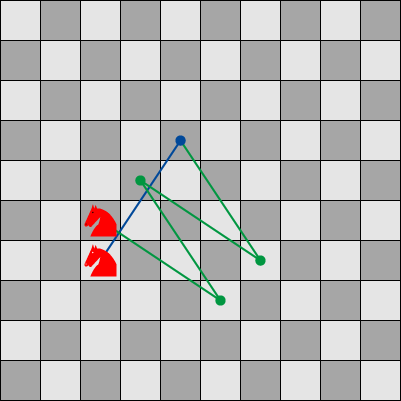
Opgave 404 [ooO]

Dit is zeker mogelijk. Als het $(2, 3)$ paard naar rechts $3$ en naar beneden $2$ springt en vervolgens naar links $2$ en naar boven $ 3$ dan springt het paard in twee sprongen één vakje naar rechts en één vakje naar boven. Herhaal dit procedé tweemaal en zet het paard met één sprong terug in de richting waar het paard vandaan kwam.