Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 20 augustus 2019.

Opgave 405 [oOO]

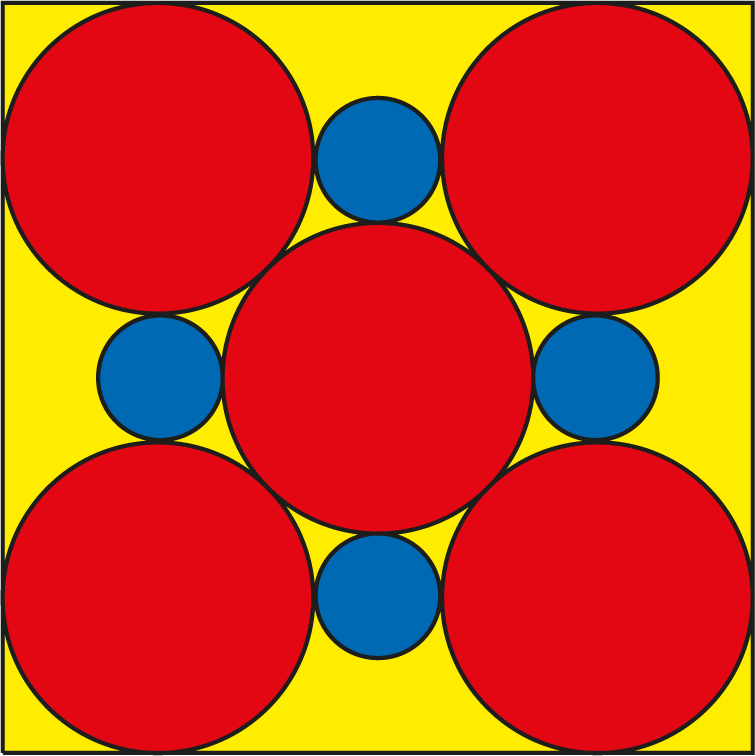
In een vierkant met zijde 6 worden vijf rode cirkels geplaatst, zó dat vier cirkels raken aan steeds twee zijden en de laatste cirkel raakt aan de overige vier cirkels.

Vervolgens worden nog vier blauwe cirkels geplaatst die raken aan de middelste cirkel en steeds twee andere.

Bepaal de stralen van de rode en blauwe cirkels.

Opgave 406 [oOO]

Hierboven zie je een schaakbord waarvan een aantal velden zijn verwijderd. Op een willekeurig veld wordt een toren geplaatst. Een torenrondgang is een opeenvolging van zetten van de toren (horizontaal of verticaal, niet diagonaal), waarbij elk veld precies één keer wordt bezocht en waarbij het eerste en laatste veld hetzelfde zijn. Is een torenrondgang op dit bord mogelijk? Zo ja, hoe ziet die rondgang eruit? Zo nee, hoeveel velden worden dan minstens niet bezocht?

Opgave 407 [ooO]

Bewijs dat voor elke geheel getal n > 1 geldt dat

$$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots+\frac{1}{n^2} > \frac{3n}{2n+1}.$$

Opmerking: Er geldt dat de oneindige som

$$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots+\frac{1}{n^2} + \cdots = \frac{\pi^2}{6}.$$

Zie Wikipedia: Bazel-probleem.

Opgave 408 [ooO]

We zetten in een (eindig groot) rooster op een aantal vakjes een spiegel neer, deze wordt dan diagonaal onder een hoek van $45^{\circ}$ geplaatst. We sturen hier een lichtstraal parallel in het rooster in. Bepaal een bovengrens voor hoe lang het duurt voor een lichtstraal weer het rooster verlaat.

In het voorbeeld hieronder is de lengte van de lichtstraal in het rooster van $5 \times 5$ gelijk aan $26.$

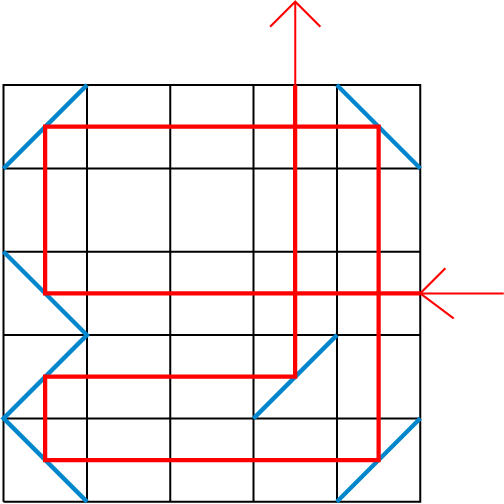
Bestaat deze bovengrens ook als de lichtstraal niet meer parallel aan het rooster naar binnen gaat?

Bij deze opgave kun je ook punten krijgen voor deeloplossingen. Bovendien geven we bonuspunten voor een fraaie oplossing.

Bekijk oplossing