Opgave 405 

We noemen de straal van de rode cirkel $r$ en die van de blauwe cirkel $b$. Er geldt dat $4r + 2b = 6$. De diagonaal van het vierkant met zijde $2r + 2b$ heeft de lengte $4r$. Volgens Pythagoras, (toegepast op een rechthoekige gelijkbenige driehoek) geldt dus $2r + 2b = 2r\sqrt 2$. Zodoende vinden we $b = r(\sqrt 2 - 1)$. Na substitutie van $b$ in de eerste vergelijking vinden we $4r + 2r(\sqrt 2 - 1) = 6$,  ofwel $$r=\frac{3}{1+\sqrt2} = 3(\sqrt2-1).$$ Hieruit volgt $b = 3(3 - 2\sqrt 2)$.

Opgave 406

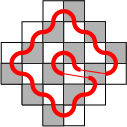
Een koning zou geen koningsrondgang kunnen maken. De koning kan twee velden niet bereiken. Een toren moet op die plaatsen een veld overslaan (dat is met een dunne rode lijn weergegeven).

Opgave 407

Laat in deze opgave $$S_n = \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots +\frac{1}{n^2}.$$
We bewijzen deze opgave met volledige inductie.

De eerste stap (inductiebegin) is het controleren of de ongelijkheid geldt voor $ n = 2$. Dat is inderdaad het geval, immers $1 + \frac{1}{2^2} = \frac54 > \frac65$.

De inductieveronderstelling is dat voor een zekere $n$ geldt dat $ S_n > \frac{3n}{2n+1}$.

De inductiestap die we nu moeten bewijzen is of dan daaruit volgt dat $S_{n+1}>\frac{3(n+1)}{2n+3}$.

Dat is inderdaad het geval, want $S_{n+1}=S_n+\frac{1}{(n+1)^2}$. We hebben:

$$S_{n+1}=S_n+\frac{1}{(n+1)^2}>\frac{3n}{2n+1}+\frac{1}{(n+1)^2}\ge\frac{3(n+1)}{2n+3}.$$

Deze laatste ongelijkheid moeten we natuurlijk nog wel bewijzen. Eerst trekken we rechts en links $\frac{3n}{2n+1}$ af. Tevens brengen we de twee noemers aan de rechter zijde samen.

$$\frac{1}{(n+1)^2}\ge\frac{3(n+1)}{2n+3}-\frac{3n}{2n+1}=\frac{3}{(2n+1)(2n+3)}.$$

Vervolgens vermenigvuldigen we de ongelijkheid met de noemers aan weerszijden: $$ (2n + 1) (2n + 3) \ge 3(n + 1)^2.$$

Als we de haakjes uitwerken, dan blijkt dat deze ongelijkheid inderdaad klopt, en daarmee is de inductiestap bewezen.

Opgave 408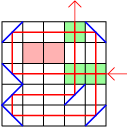

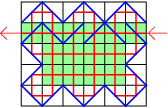
We kunnen in één vakje lengte $0$, $1$ of $2$ aan lichtstraal hebben. We kleuren de velden rood als er in de betreffende velden geen lichtstraal is, en we kleuren een veld groen als in het betreffende veld lichtstralen ter lengte $2$ zijn. Zie het voorbeeld hiernaast. We gaan uit van een rooster met afmetingen $a$ en $b$. We onderscheiden de rand en het binnengedeelte. In het binnen gedeelte kunnen in één veld maximaal twee stralen aanwezig zijn, in de rand is dat er maar één, behalve de velden waar de straal naar binnen gaat en er weer uit komt. Zodoende is het theoretische maximum $ab + (a-2)(b-2)+2=2ab-2a-2b+6$.

We onderscheiden $6$ gevallen ($a \le b$):

• $a = 1 $
• $a = b = 2 $
• $a = 2$ en $b > 2$
• $a$ en $b$ zijn even (groter dan $2$)
• $a$ of $b$ is even, de ander oneven
• $a$ en $b$ zijn oneven.

Voor elk van deze gevallen moet worden nagegaan of het optimale maximum ook gehaald wordt.

Geval: $a = 1$ De maximale lichtstraallengte is $b$.
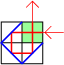
Geval: $a = b = 2$ De maximale lichtstraallengte is $5$.
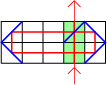
Geval: $a = 2$ en $b$ > 2$ De lichtstraallengte heeft de maximale lengte van $2b+2$ (is optimaal!)
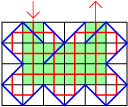
Geval: $a$ en $b$ zijn even We kunnen nu spiegels in de randvelden plaatsen die het binnengedeelte helemaal afsluiten. Er zijn weliswaar een aantal losse gesloten routes, maar door een aantal spiegels te plaatsen is het mogelijk om één gesloten route te creëren, die alle velden van het binnengedeelte dubbel meeneemt. Ten slotte maken we twee openingen naar buiten en verschuiven we een paar spiegels. De lichtstraallengte heeft de maximale lengte van $2ab - 2a - 2b + 6$ (is optimaal!)
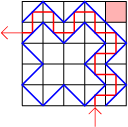
Geval: $a$ of $b$ is even, de ander oneven Laten we voor het gemak $a$ (horizontaal) even zijn en $b$ oneven (verticaal). Als we de bovenste strook velden weglaten, dan kunnen we de resterende velden rondom het binnengebied plaatsen. In de bovenste rij kunnen we nog $a$ extra spiegels plaatsen. De spiegels worden geplaatst zoals hieronder is weergegeven. Er kan een lichtstraal doorheen. Nu moeten we opnieuw door spiegels te plaatsen (verwijderen en verplaatsen) de lichtstraal (zoals hierboven is getekend) combineren met de lichtstraal in het gesloten deel. Dat lukt bijvoorbeeld met deze oplossing: Ook hier heeft de lichtstraallengte de maximale lengte van $2ab - 2a - 2b + 6$ (is optimaal!)
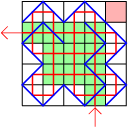
Geval: $a$ en $b$ zijn oneven We kunnen linksonder een gesloten deel creëren. Boven en rechts plaatsen we nog extra spiegels. Dit gebeurt op een dusdanige manier dat het veld rechtsboven niet kan worden bereikt door een lichtstraal. Het theoretische maximum zal niet worden bereikt. Een lichtstraal die rechtsonder het vierkant in gaat verlaat het vierkant linksboven. Deze lichtstraal moet worden gecombineerd met de gesloten route in het gesloten deel. Dit lukt door één spiegel te verwijderen. De lichtstraallengte heeft nu lengte $2ab - 2a - 2b + 5$ (is optimaal!) In deze oplossing komt het verplaatsen van spiegels, zodat de maximale lengte wordt bereikt niet goed uit de verf. De ruimte hier is ontoereikend om dat op papier te zetten. Dat geldt ook voor het feit dat in geval van oneven bij oneven het maximum niet kan worden bereikt.

Extra opgave.

Door twee spiegels parallel te plaatsen en een lichtstraal min of meer loodrecht op de spiegel te plaatsen kan de lengte van de lichtstraal oneindig groot worden. (Theoretisch gezien! Fysische wetten maken dit onmogelijk.)