Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 9 november 2019.

Opgave 409 [oOO]

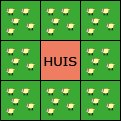In een mooi stallencomplex zit in het midden een schaapherder die nauwlettend zijn lieve schaapjes in het oog houdt. In elke stal zitten vijf schapen, zoals op de tekening afgebeeld staan. 
In de middelste ruimte zitten vier ramen, waar de herder door kan kijken. Via elk raampje ziet hij vijftien schapen (drie stallen van elk vijf schapen). 

Nu arriveert er een nieuwe lading schapen. In totaal zijn er zestien nieuwe schapen, die ook in de stallen moeten worden geplaatst. Maar dat moet zo gebeuren, dat de schaapherder uit elk raampje nog steeds vijftien schapen blijft zien. Het is toegestaan om de schapen uit de kooien te verplaatsen. Het is niet toegestaan om de brave diertjes te slachten. 

Er moet minstens één schaap in elke stal zitten. Hoe moeten de schapen verdeeld worden over de stallen?

Opgave 410 [oOO]

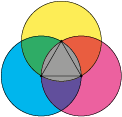Bepaal de oppervlakte van het grijs gearceerde deel van de tekening hiernaast. De middelpunten van de cirkels liggen op de hoekpunten van een gelijkzijdige driehoek met zijde $1.$ Ook de stralen hebben lengte $1.$

Opgave 411 [ooO]

Maarten kiest één van de tweecijferige priemgetallen en geeft Erik het eerste cijfer van dit priemgetal en hij geeft Laura het laatste cijfer. Maarten vraagt vervolgens “Weten jullie welk priemgetal ik heb gekozen?”

Erik zegt: “Ik weet het niet”, Laura zegt: “Ik weet het ook niet, en trouwens ik wist al dat jij het niet zou weten”. Hierop zegt Erik: “Maar nu weet ik wel welk priemgetal Maarten heeft gekozen”. Weet Laura nu ook welk priemgetal Maarten heeft gekozen?

Opgave 412 [ooO]

Kees heeft drie bekertjes naast elkaar op tafel staan. Alle drie liggen op z'n kop, en onder de middelste ligt een euro. Vervolgens verwisselt hij $100$ keer ofwel de middelste en de linker, ofwel de middelste en de rechter. De kans dat hij het ene paar omwisselt of het andere is steeds $\frac12.$ Is na afloop de kans dat de euro weer in het midden ligt groter dan $\frac13,$ precies $\frac13$ of kleiner dan $\frac13?$

 

Bekijk oplossing