Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 15 december 2019.

Opgave 413 [oOO]

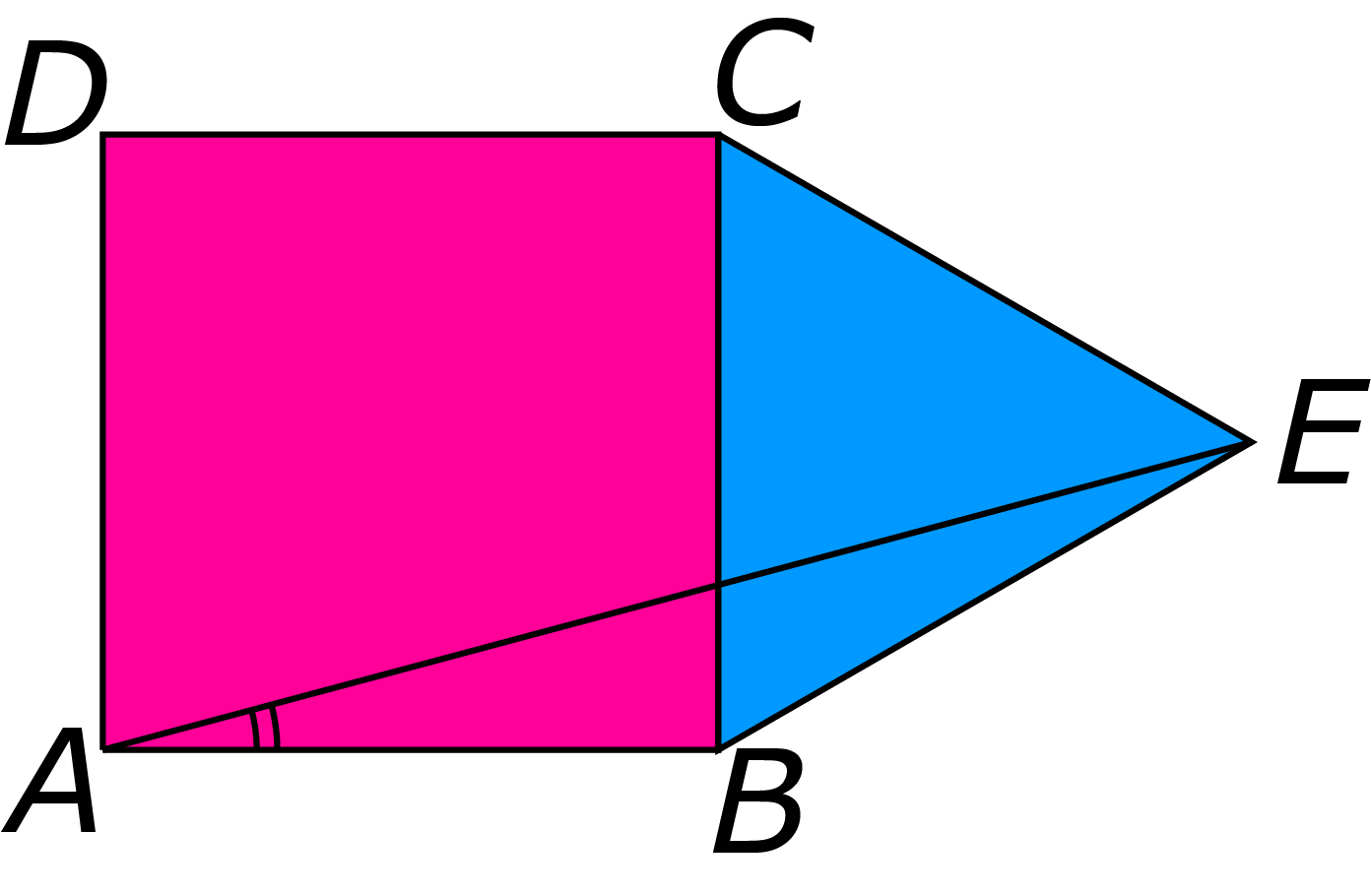Gegeven is het vierkant $ABCD.$ Op de zijde $BC$ staat een gelijkzijdige driehoek $BCE.$ Bepaal de hoek $\angle BAE.$

 

 

Opgave 414 [oOO]

Laura gaat verhuizen naar de stad waar ze al een jaar studeert. Op de Campusweg wonen inmiddels haar 9 beste vriendinnen. De onderlinge afstanden van haar vriendinnen (die allen in verschillende huizen wonen) is aangegeven. Waar gaat haar voorkeur naar uit als haar wens is om de som van de afstanden tot haar vriendinnen te minimaliseren?

Opgave 415 [ooO]

In een laboratorium is een flesje met het pokkenvirus terecht gekomen bij een verzameling van 125 verder identieke flesjes mazelenvaccin. Helaas kan niet meer achterhaald worden welk flesje het pokkenvirus bevatte. Er wordt berekend dat het het goedkoopst is om een aantal kweken te maken. Dat kan van de inhoud van één of meer flesjes zijn. De resultaten van een dergelijke kweek geven met 100% zekerheid dat in één van de flesjes het pokkenvirus zat, als dat flesje wordt getest. Het kost echter 24 uur voordat de resultaten bekend zijn. De directeur van het laboratorium eist dat:

• er over 24 uur bekend is welk flesje het pokkenvirus bevat,
• het aantal kweken zo laag mogelijk wordt gehouden,
• minimaal één van de kweken het pokkenvirus moet bevatten, om zo zekerheid te hebben dat het flesje gevonden is.

Hoe pakt de laborant dit probleem aan?

Opgave 416 [ooO]

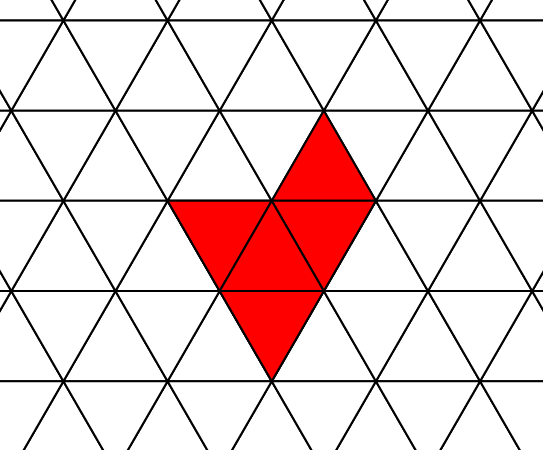Rechts staat een figuur bestaande uit 5 gelijkzijdige driehoeken. Maak een vlakvulling met deze figuur (en het spiegelbeeld van deze figuur).

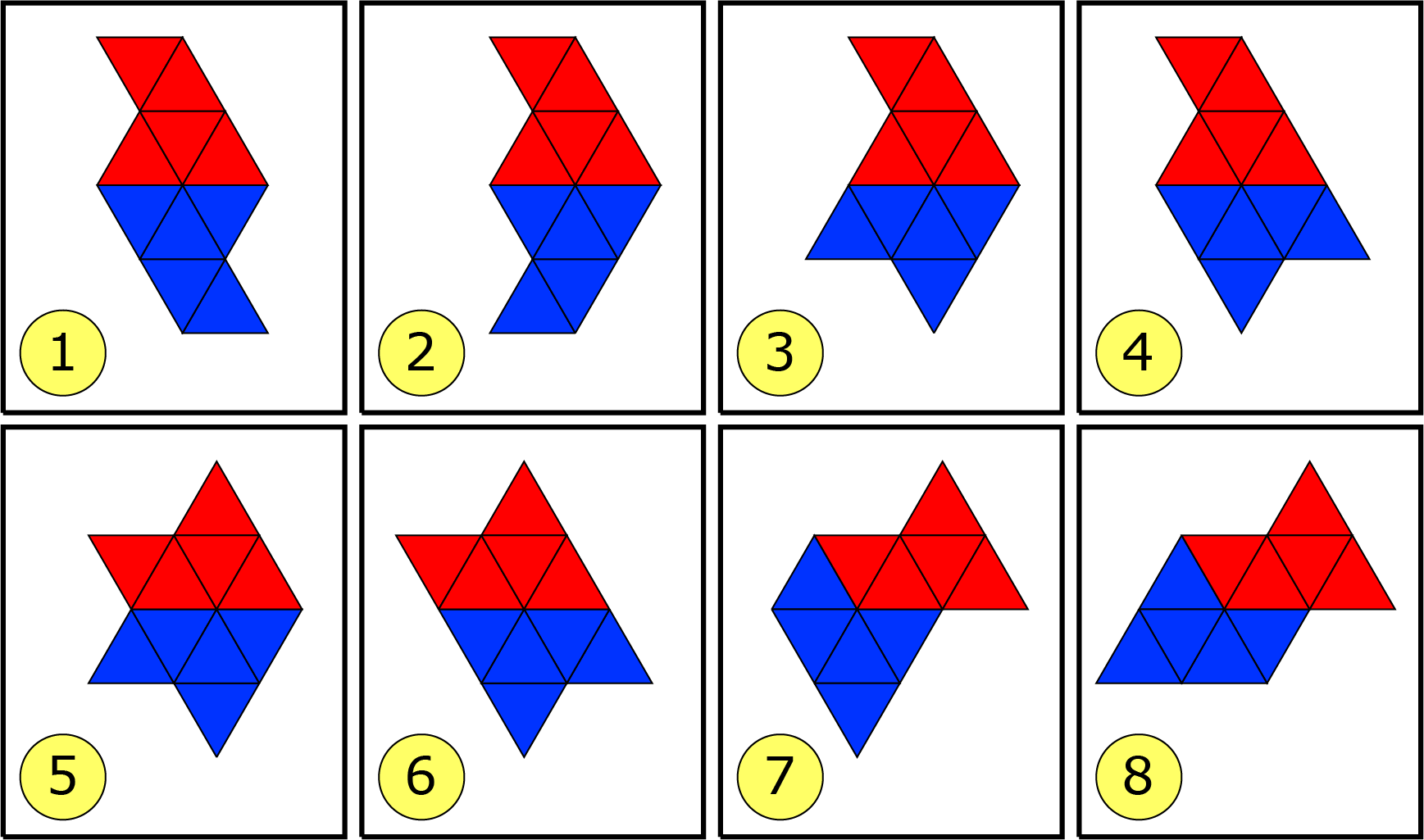
Voor één of twee bonuspunten: in de figuur hieronder staan alle mogelijkheden hoe je twee figuren met 5 gelijkzijdige driehoeken aan elkaar kunt leggen, zó dat er twee zijden aan elkaar liggen. Probeer met zoveel mogelijk van deze figuren (bestaande uit 10 gelijkzijdige driehoeken) vlakvullingen te leggen. (Het zal niet met alle figuren lukken.)

 

 

 

 

 

 

 

 

 

 

Bekijk oplossing