Opgave 413

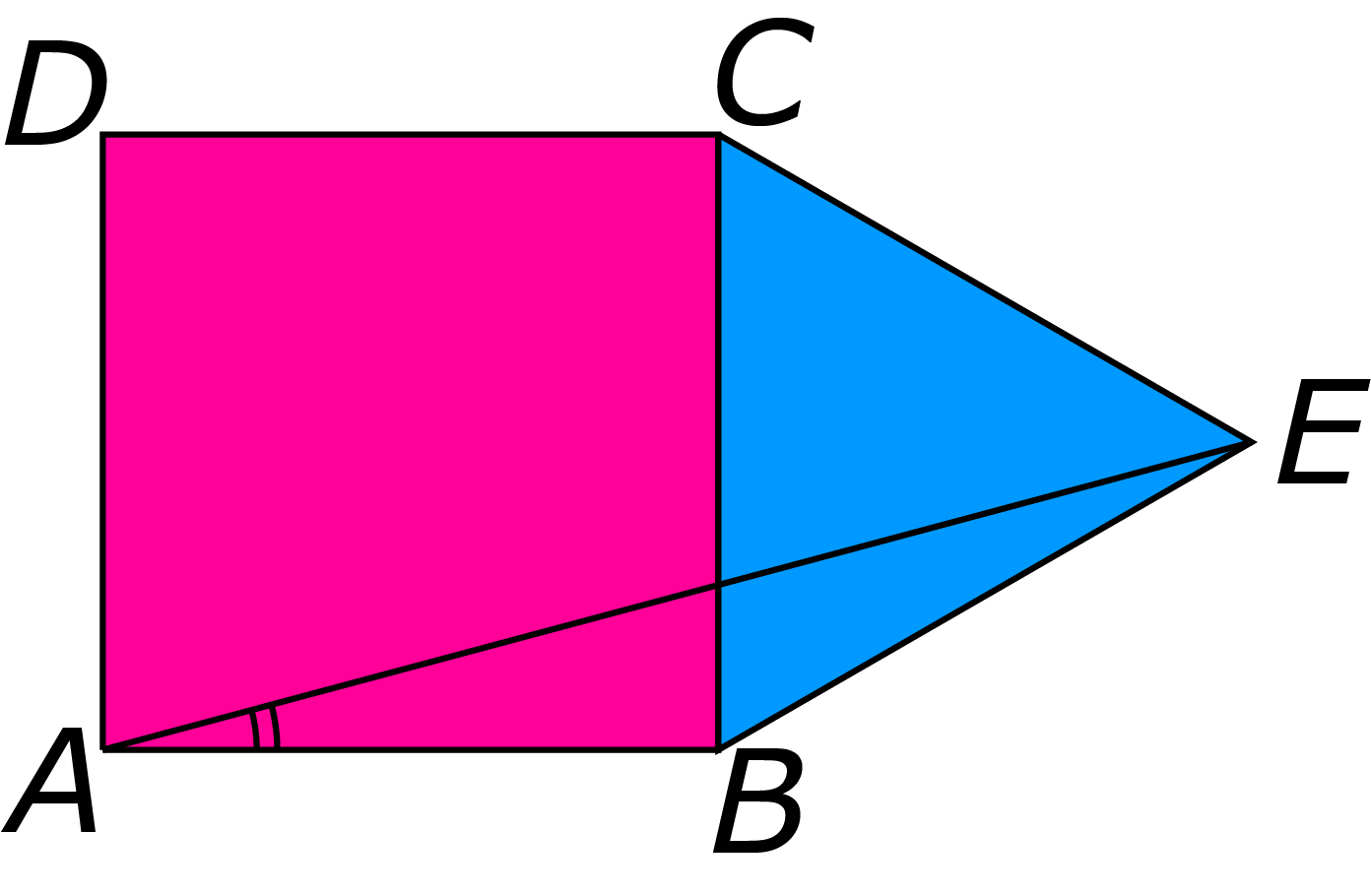
Omdat $ABCD$ een vierkant is, geldt dat $\angle ABC = 90^{\rm o}$ en $|AB| = |BC|$. Omdat $BEC$ een gelijkzijdige driehoek is, geldt dat $\angle EBC = 60^{\rm o}$ en $|BC| = |BE|$. Als we dit combineren, dan vinden we dat $\angle ABE = \angle ABC + \angle EBC = 90^{\rm o} + 60^{\rm o} = 150^{\rm o}$ en bovendien dat $|AB| = |BC| = |BE|$. We concluderen dat driehoek $ ABE$ een gelijkbenige driehoek is met een tophoek van $150^{\rm o}$. Voor de basishoek vinden we dan dat $\angle BAE = (180^{\rm o} - 150^{\rm o})/2 = 15^{\rm o}$.

Opgave 414

Veronderstel dat Laura zich links van het huis van vriendin $E$ bevindt. Als zij nu een meter naar rechts beweegt, dan verkleint de afstand tot de huizen van vriendinnen $ E, F, G, H$ en $I$ met een meter, terwijl de afstand tot de vriendinnen $A, B, C$ en $ D$ ofwel toeneemt met een meter, ofwel afneemt met een meter. Er zullen dus zeker meer vriendinnen zijn ten opzichte van wie de afstand een meter kleiner wordt, en dus zal de totale som van de afstanden tot de vriendinnen afnemen. Op volkomen analoge wijze redeneren we dat indien Laura zich rechts van het huis van vriendin $E$ bevindt, een stap naar links zetten de totale som van de afstanden tot haar vriendinnen zal doen afnemen. Als we dit combineren, concluderen we dat Laura het beste bij vriendin $E$ in huis kan gaan wonen.

Opgave 415

Nummer de flesjes van $1$ tot en met $125 $ en vertaal deze getallen vervolgens naar het binaire stelsel. Zo kunnen we elk flesje een unieke code van precies zeven nullen en enen toekennen, omdat $2^7 = 128 > 125 $Beschouw nu zeven verschillende kweken. De eerste kweek bevat alle flesjes die een $ 1$ op de eerste positie van hun nummer hebben, de tweede bevat alle flesjes die een $1$ op de tweede positie van hun getal hebben, en zo verder tot de zevende kweek. Na $24$ uur zal een aantal kweken tekenen van het pokkenvirus vertoond hebben. Deze kweken komen precies overeen met de enen die voorkomen in de binaire schrijfwijze van het nummer dat het flesje met het pokkenvirus gekregen heeft. Omdat ieder flesje een uniek nummer gekregen had, vinden we uit deze informatie zo het flesje met het pokkenvirus terug.

Opgave 416

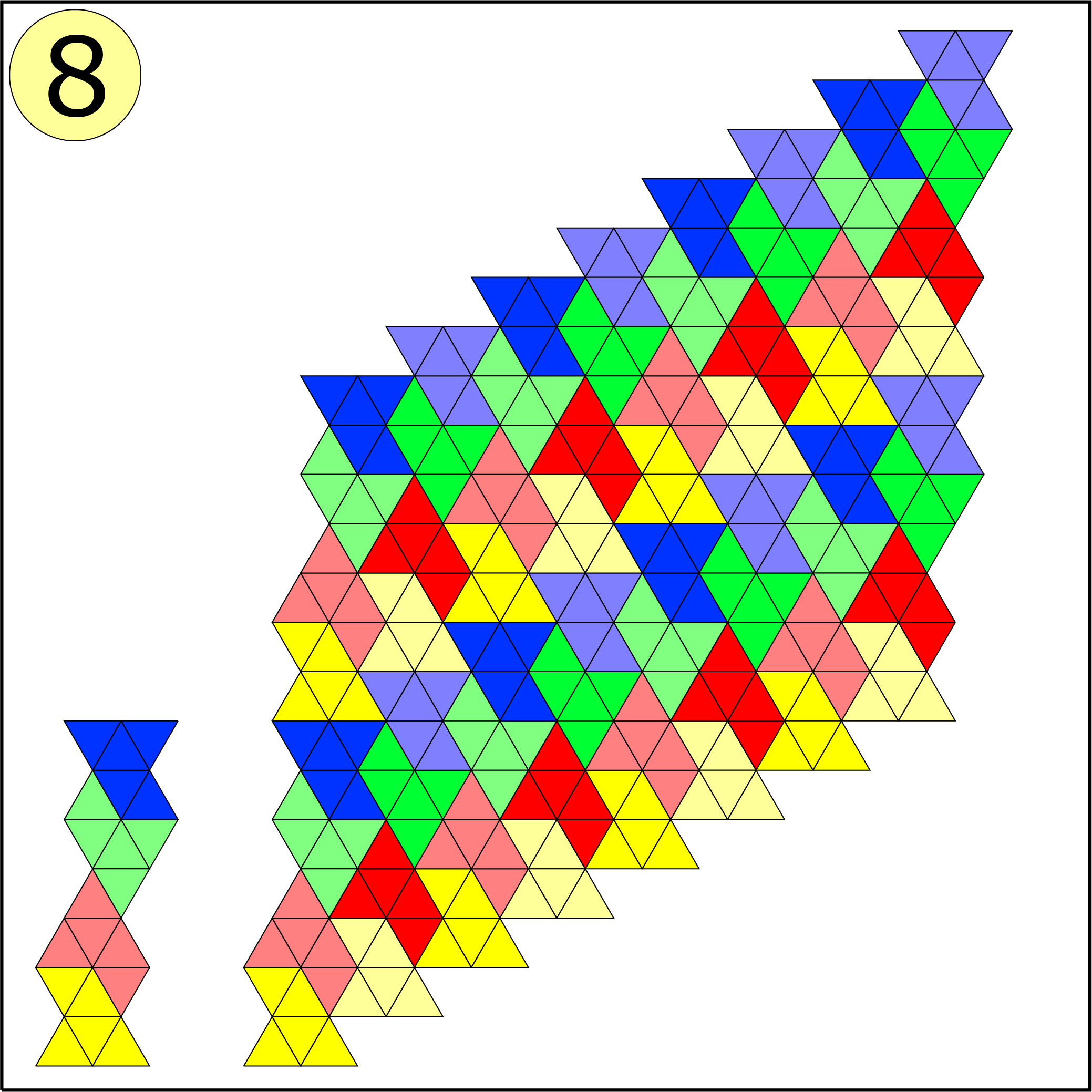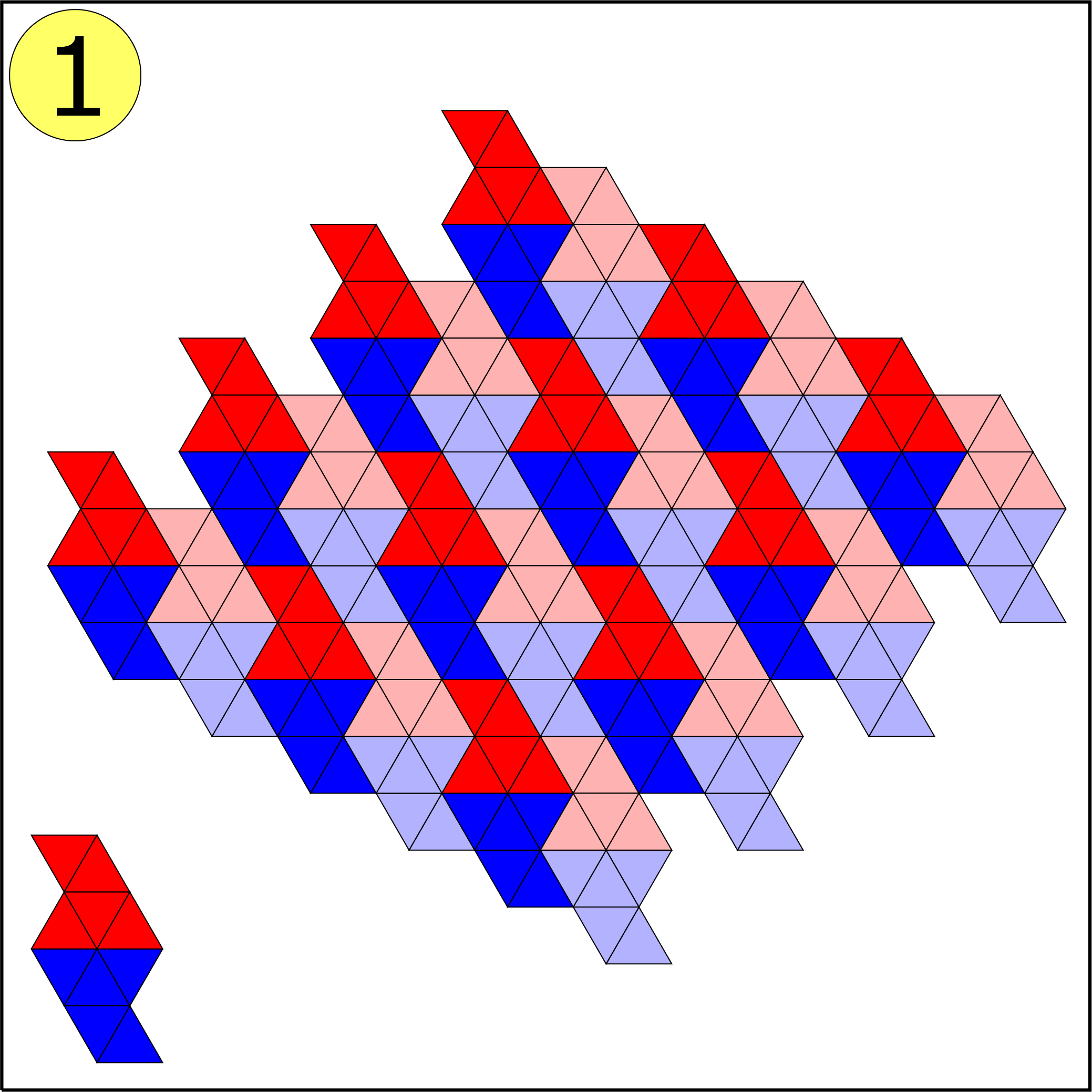
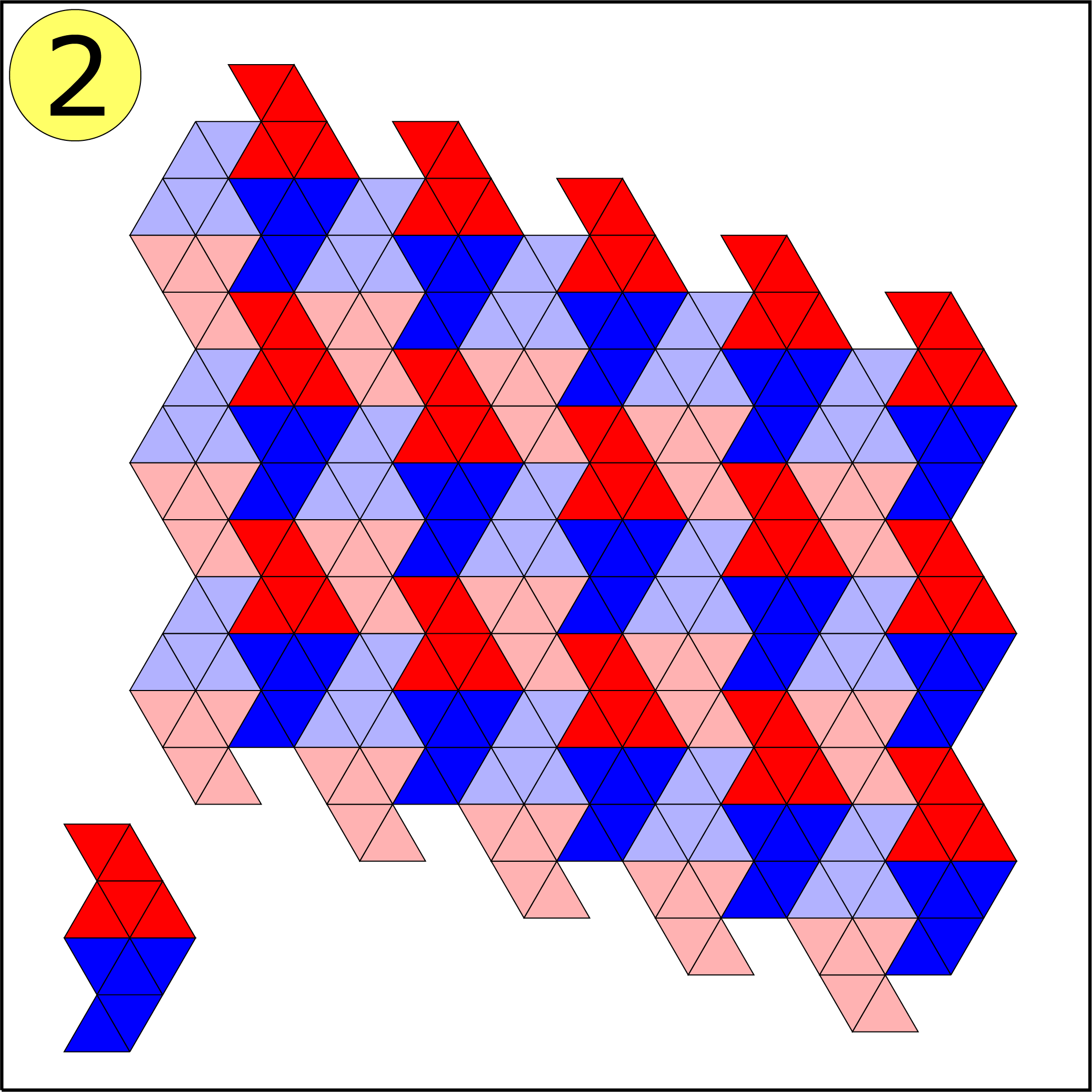
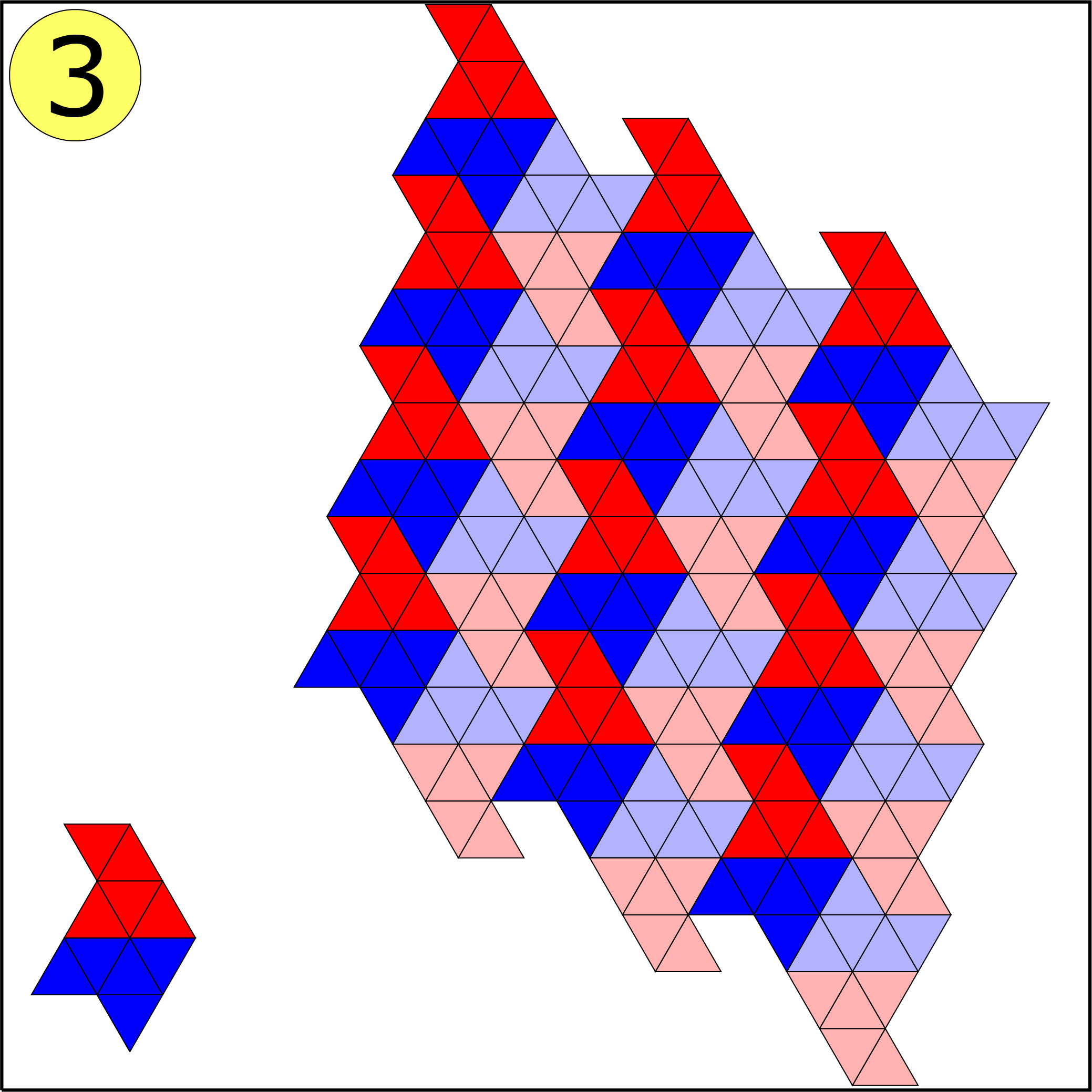
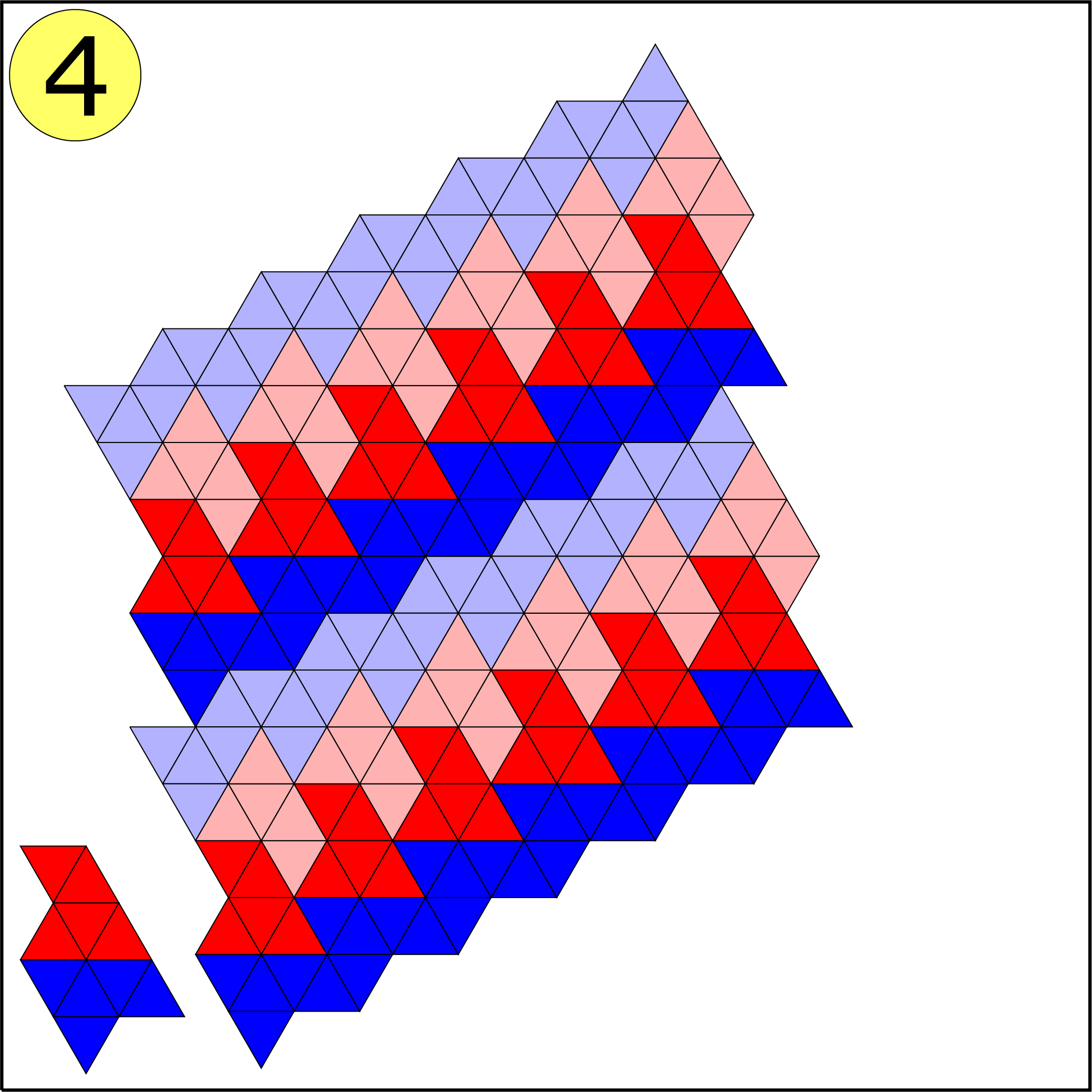
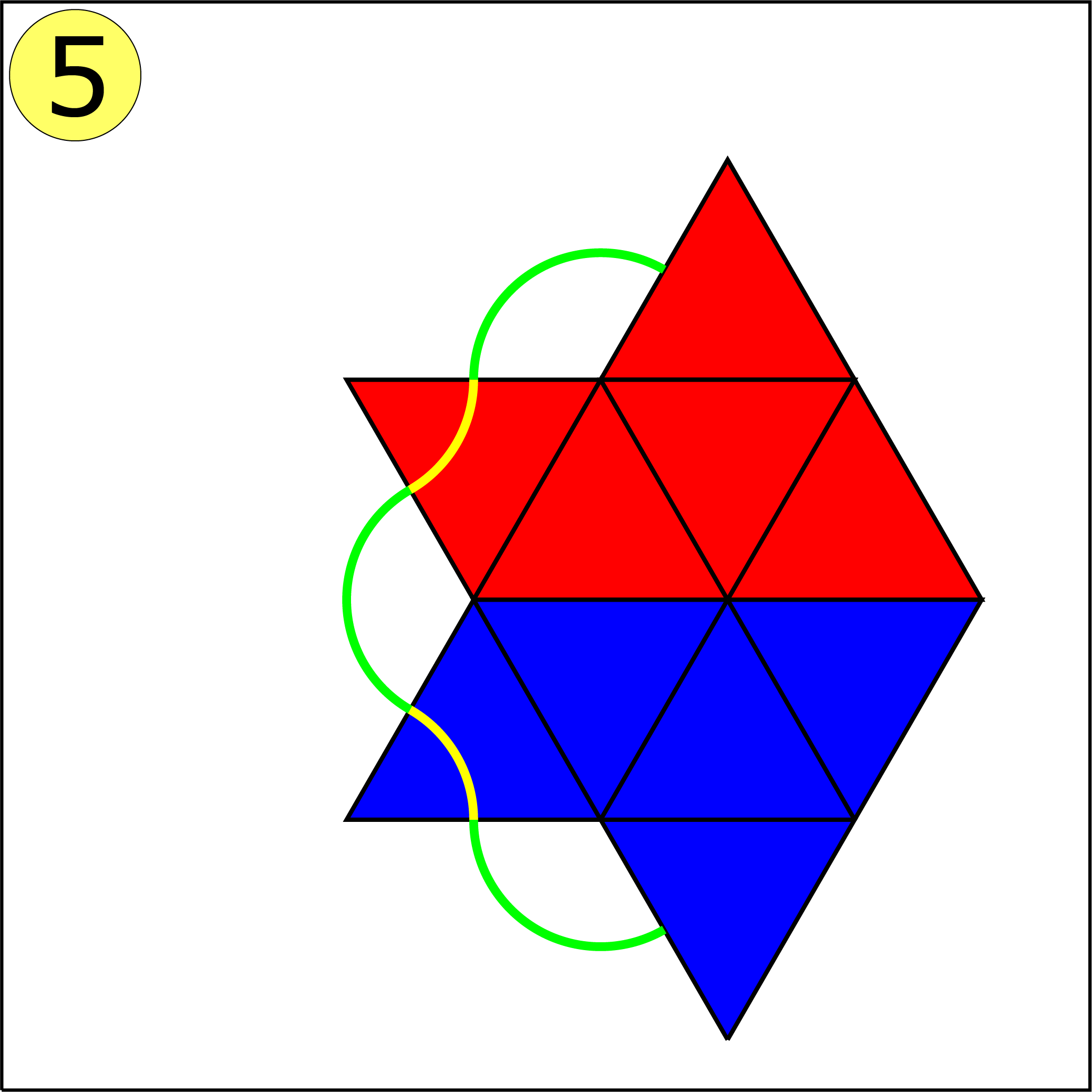
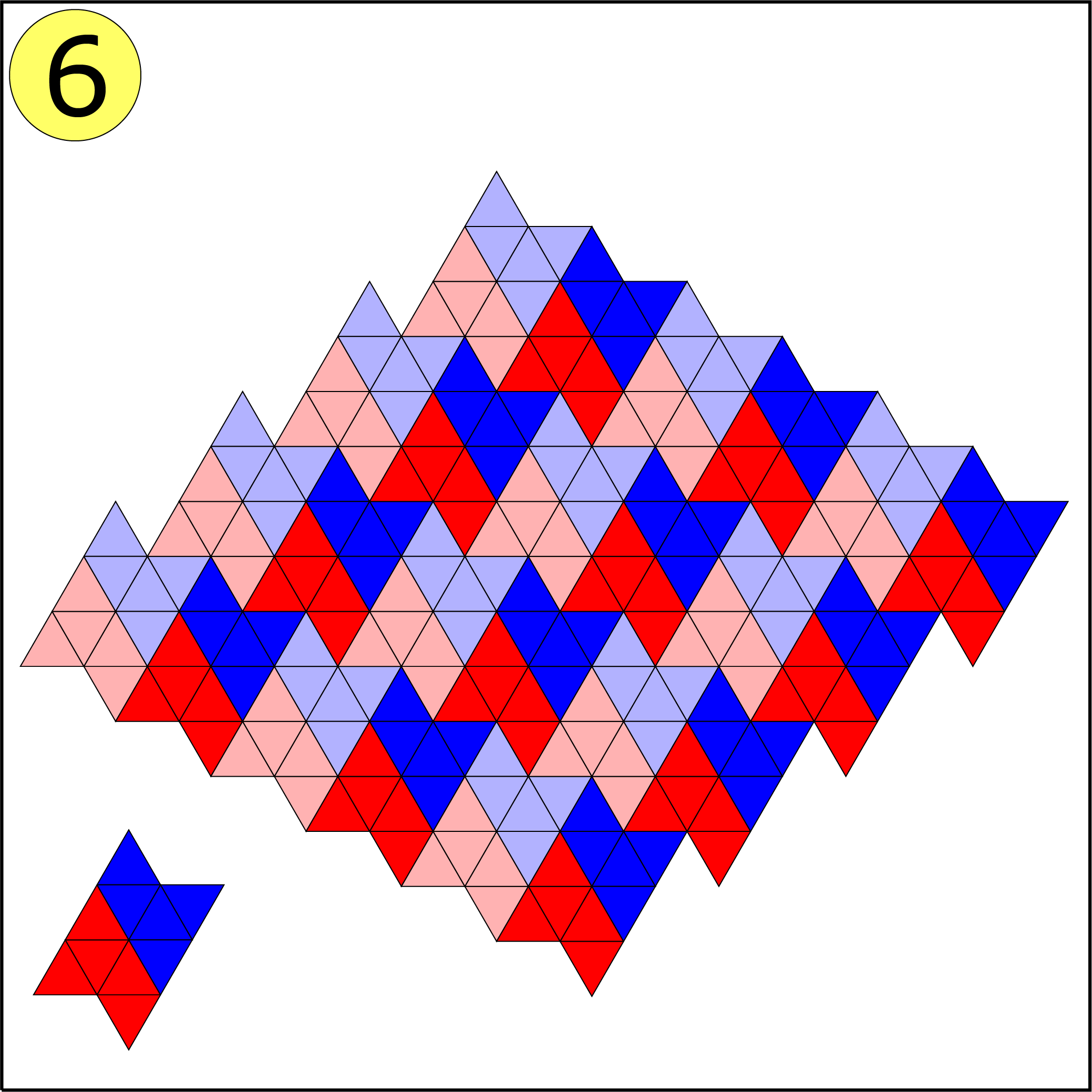
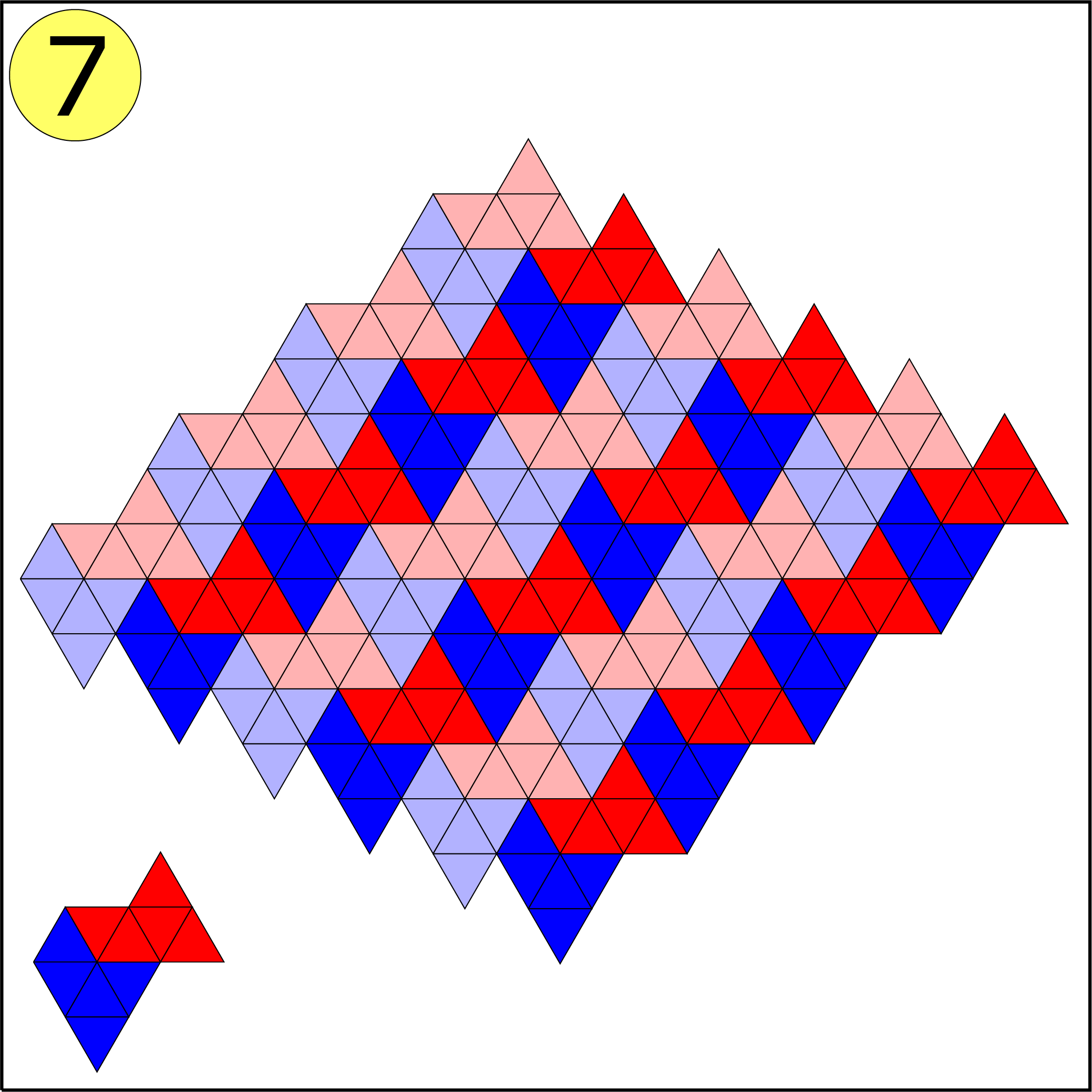
Bij de vijfde figuur lukt het niet. Lance Bakker (klas 2, Katholieke Scholengemeenschap, Hoofddorp) bewees tevens waarom het niet lukt. Zijn bewijs komt er op neer dat figuur 5 drie hoeken van $240^{\rm o}$ bevat. Om te komen tot een volledige vlakvulling moeten deze hoeken worden aangevuld met een hoek van $120^{\rm o}$ of twee hoeken van $60^{\rm o}$. Figuur 5 bevat echter vier hoeken van $ 60^{\rm o}$ en één hoek van $120^{\rm o}$. Daarmee kunnen precies drie hoeken worden opgevuld. Het probleem is echter dat de twee (met geel gemarkeerde) hoeken van $60^{\rm o}$ op geen enkele manier met een andere hoek kunnen worden samengevoegd tot een hoek van $ 120^{\rm o}. $ Bij de vlakvulling in figuur 4 moet je de helft van de figuren spiegelen. (In de opgave was dit niet helemaal duidelijk.)