Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 1 juli 2020.

Opgave 425 [niveau oOO]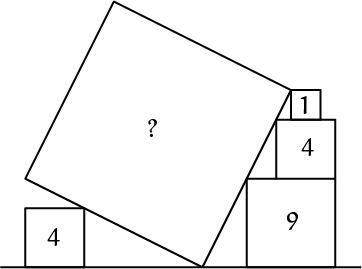

We plaatsen een gedraaid vierkant tegen een vierkant (links) en een stapel vierkanten (rechts), zie de figuur. Het vierkant links heeft oppervlakte $4, $ terwijl de toren van vierkanten rechts bestaat uit vierkanten met oppervlakte $9, 4$ en $1$. De rechterzijde van het vierkant met oppervlakte $4$ sluit aan op de rechterzijde van het vierkant met oppervlakte $ 9$. Het gedraaide vierkant heeft een hoekpunt gemeen met het vierkant met oppervlakte $1$. Wat is de oppervlakte van het gedraaide vierkant?

(Met dank aan Ben Orlin)

Opgave 426 [niveau oOO]

We schrijven de getallen $1$ tot en met $1000$ achter elkaar op. Hoeveel keer komt het cijfer $0$ voor in het resultaat?

Opgave 427 [niveau ooO]

Een boer bezit een gebied dat bestaat uit vierkante graanvelden die liggen in een rechthoek van $3$ bij $4 $ velden. Op een dag merkt hij op dat al zijn velden vol zitten met muizen en besluit hij om alles muisvrij te maken, waarbij hij linksonder begint. De boer kan per dag driemaal naar een aangrenzend veld bewegen. Alle vier de velden die de boer zo per dag bezoekt, maakt hij muisvrij. Het veld waar hij gisteren geëindigd was, is het eerste veld dat hij de volgende dag weer muisvrij maakt. Echter, ’s nachts breiden de muizen zich weer uit naar alle velden die grenzen aan een nog niet-muisvrij gemaakt veld. Er komen geen muizen van buiten het perceel zijn velden binnen.Kan de boer het hele gebied muisvrij maken? Zo ja, binnen hoeveel dagen kan de boer dat bewerkstelligen?

Opgave 428 [niveau ooO]

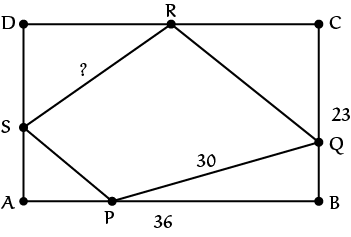
Zij $ABCD$ een rechthoek met $|AB| = 36$ en $|AD| = 23$. Voor de vierhoek $PQRS$ is gegeven dat de hoekpunten daarvan respectievelijk op de zijden $AB, BC, CD$ en $DA$ liggen en daarbij niet samenvallen met de punten met de punten $A, B, C$ en $D$. De afstanden van $P$ tot $A$ en $B$ zijn geheel. Hetzelfde geldt voor de afstanden van $Q$ tot $B$ en $C$, de afstanden van $R$ tot $C $ en $D$ en de afstanden van $S$ tot $D$ en $A$. Tevens geldt dat de lengtes van de zijden van $PQRS$ verschillende gehele getallen zijn en dat $|PQ| = 30$. Hoe lang is lijnstuk $RS?$

(Met dank aan Huub Odijk)

 

 

 

Bekijk oplossing