Opgave 425 [oOO]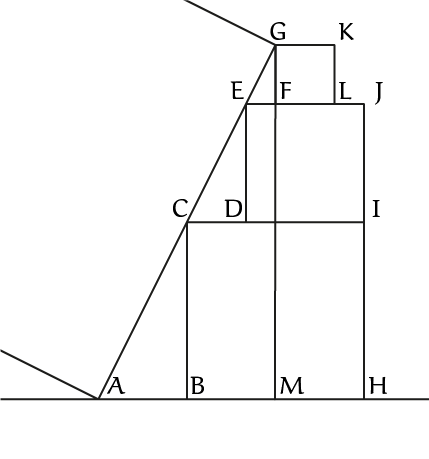

We bepalen de lengte van de schuine zijde die tegen de drie vierkanten aan ligt: in de figuur is dit lijnstuk $AG$. Aangezien de oppervlakte van vierkant $BHIC$ gelijk is aan $9,$ is de zijde gelijk aan $3,$ en zo volgt dus $|CI| = 3$. De oppervlakte van $DIJE$ is gelijk aan 4, dus $|DE| = |DI| = 2$, waaruit volgt $|CD| = 1$. We vinden ook dat $|GM| = 1 + 2 + 3 = 6$. Via F-hoeken zien we dat $\angle CED = \angle CGM = \angle AGM$, en ook $\angle CDE = 90^{\rm o} = \angle AMG.$ Dus $\triangle CDE \sim \triangle AMG\,\,(hh)$. Hieruit volgt dat $|AM|/|GM| = |CD|/|ED| = \frac{1}{2}$ en dus geldt $|AM| = 3$. De stelling van Pythagoras geeft ons nu dat $|AG| = \sqrt{6^2 + 3^2} = \sqrt{45}$, en dus is de oppervlakte van het gevraagde vierkant gelijk aan $(\sqrt{45})^2 = 45$.

Opgave 426 [oOO]

Er zijn verschillende manieren om dit slim te tellen. Eén manier is door te kijken hoeveel keer het cijfer van respectievelijk de eenheden, tientallen en honderdtallen $0$ is:

• Het cijfer van de eenheden (het laatste cijfer) is $0$ voor alle tienvouden. Aangezien er $100$ tienvouden zijn in de getallen van $1$ tot $1000$, geeft dit ons $100$ nullen.
• Het cijfer van de tientallen is $0$ voor alle getallen van de vorm $x0y$ met $x \neq 0$, en er zijn $90$ zulke getallen. Het is ook $0$ bij $1000$. Dus in totaal is dit cijfer $91$ keer $0$.
• Het cijfer van de honderdtallen is alleen $0$ voor $1000$. Dus $1$ keer.

Dus we tellen in totaal $100 + 91 + 1 = 192$ nullen.

Opgave 427 [ooO]

Het antwoord is ja, de boer kan het hele veld muisvrij maken. Hij heeft hiervoor minstens 9 dagen nodig. Een voorbeeld van een plan om het veld muizenvrij te maken is te zien in de figuur.

Hierbij bezoekt de boer op dag $1$ alle velden met nummer $1,$ waarbij hij start op het veld linksonder. Op dag $2$ bezoekt hij alle velden met nummer $2,$ startend op het veld waar hij op dag $1$ eindigde. Enzovoorts, tot aan dag $9.$ Na $9$ dagen is het hele veld dan muizenvrij. Je kan dit controleren door het dag voor dag uit te tekenen.

We kunnen ook bewijzen dat het niet nog beter kan (dat was niet vereist voor de opgave). Een belangrijke observatie is het volgende: als er minstens $2$ velden zijn met muizen en minstens $2$ velden zonder muizen, dan zijn er minstens $3$ velden zonder muis die grenzen aan een veld met muis. Dit betekent dat nadat de boer op de eerste dag $4$ velden muizenvrij heeft gemaakt, er minstens $3$ weer muizen bevatten na de eerste nacht: er is er maximaal één die de volgende ochtend nog muizenvrij is. Met dezelfde redenering zien we dat er na twee dagen en nachten maximaal twee muizenvrije velden zijn. Dit gaat door tot $7$ dagen en nachten, waarna er maximaal $7$ muizenvrije velden zijn, ongeacht welke stappen de boer maakt.

Omdat de boer niet $5$ velden in een dag muizenvrij kan maken, heeft de boer na dag $7$ nog minstens $2$ dagen nodig om het hele veld muizenvrij te maken, dus de boer heeft in totaal minstens $7 + 2 = 9$ dagen nodig. Omdat deze ondergrens daadwerkelijk bereikt wordt in ons voorbeeld, is $9$ het optimale aantal dagen voor de boer.

Opgave 428 [ooO]

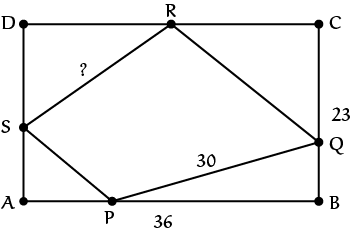
Het idee is dat je geleidelijk aan alle lengtes in de figuur uitrekent. We bekijken eerst de driehoek $BPQ$: hierin geldt $|BP|^2 + |BQ|^2 = 30^2$. De enige manier om $30^2 = 900$ als som van twee kwadraten te schrijven is $18^2 + 24^2 = 30^2$ (dit kan je vinden door uit te proberen). Omdat $|BQ| < |BC| = 23$ is het onmogelijk dat $|BQ| = 24$, dus we vinden dat $|BQ| = 18$ en dus $|BP| = 24$. Bijgevolg is $|AP| = |AB| - |BP| = 12$ en $|CQ| = |BC| - |BQ| = 5$.

Beschouw nu $\triangle CQR$. Met $|RC| = x$ en $|RQ| = y$ moeten we nu oplossen $25 + x^2 = y^2$. Dus $y^2 - x^2 = 25$ dus $(y + x)(y - x) = 25$. Aangezien $y + x > y - x$, is de enige oplossing met positieve gehele getallen dat $y + x = 25$ en $y - x = 1$. Dus $|RC| = x = 12$ en $|RQ| = y = 13$. Dus $|DR| = 24$.

Nu bekijken we $\triangle DRS$. We zoeken nu een Pythagoreïsch drietal met $24$ als rechtshoekszijde. Met dezelfde strategie als bij driehoek $CQR$ vinden we als mogelijkheden $(7, 24, 25)$, $(10, 24, 26)$ en $(18, 24, 30)$. Andere mogelijkheden hebben $|DS| > 23$ en zijn daarom onmogelijk. Omdat de zijden van $PQRS$ verschillend moeten zijn, valt $(18, 24, 30)$ af. Dus $|DS|$ is of $7$ of $10$.

We kijken tenslotte $\triangle APS$. Uit $|AP| = 12$ vinden we als mogelijke drietallen $(5, 12, 13)$, $(9, 12, 16)$ en $(12, 16, 20)$ (andere mogelijkheden hebben $|AS| > 23$). Omdat $|RQ| = 13$ valt $(5, 12, 13)$ af. We vinden dus voor $|AS|$ de mogelijke waarden $9$ en $16$.

We weten dat $|AS| + |DS| = 23$, en met de mogelijke waarden die we hebben is de enige optie hiervoor dat $|AS| = 16$ en $|DS| = 7$. We concluderen dat $|RS| = \sqrt{7^2 + 24^2} = 25$.