Opgave 433 ^{[niveau oOO]}

Oom Donald wil Kwik, Kwek en Kwak geld meegeven voor de kermis. Hij heeft $10$ muntstukken van waarde $1$, $10$ muntstukken van waarde $2$ en $10$ muntstukken van waarde $3$. Elk neefje moet in totaal evenveel geld krijgen, maar ook wil Donald elke neef evenveel muntstukken meegeven.

Op hoeveel manieren kan hij de munten in drie groepen verdelen zodat aan de voorwaarden wordt voldaan? Let op: het gaat alleen om de groepen munten en niet om welk neefje welke groep munten krijgt.

Opgave 434 ^{[niveau oOO]}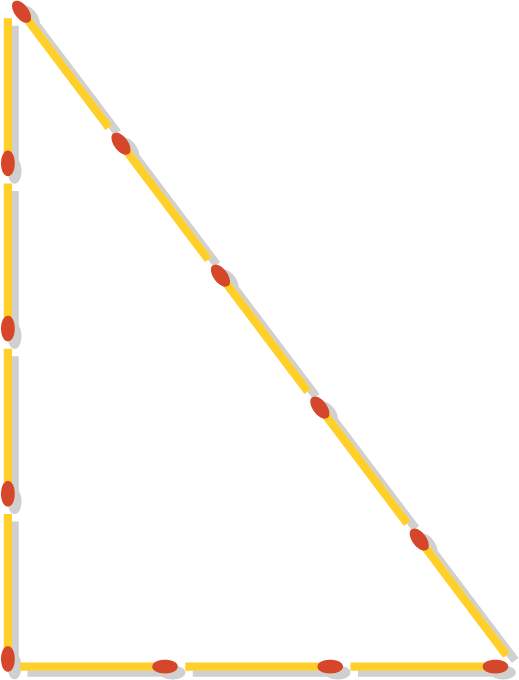

Met lucifers van lengte $1$ maken we een driehoek met zijden $3$, $4$ en $5$. Hoe kunnen we door vier lucifers te verplaatsen een figuur overhouden met oppervlakte $3$?

Opgave 435 ^{[Niveau ooO]}

Voor een positief geheel getal $n$ schrijven we de decimale expansie van $\frac1n$ als $0{,}\overline{a_1a_2a_3\ldots}$ . Bijvoorbeeld voor $n = 11$ krijg je $\frac{1}{11} = 0{,}090909\ldots$, dus $a_1 = a_3 = a_5 = \ldots = 0$ en $a_2 = a_4 = \ldots = 9$. Stel nu dat $\frac{2}{n}$ als decimale expansie $0{,}\overline{a_3a_4a_5\ldots}$ heeft, dus gelijk aan $\frac1n$ maar dan twee plekken opgeschoven. Wat zijn alle mogelijke waarden van $n$?

Opgave 436 ^{[Niveau ooO]}

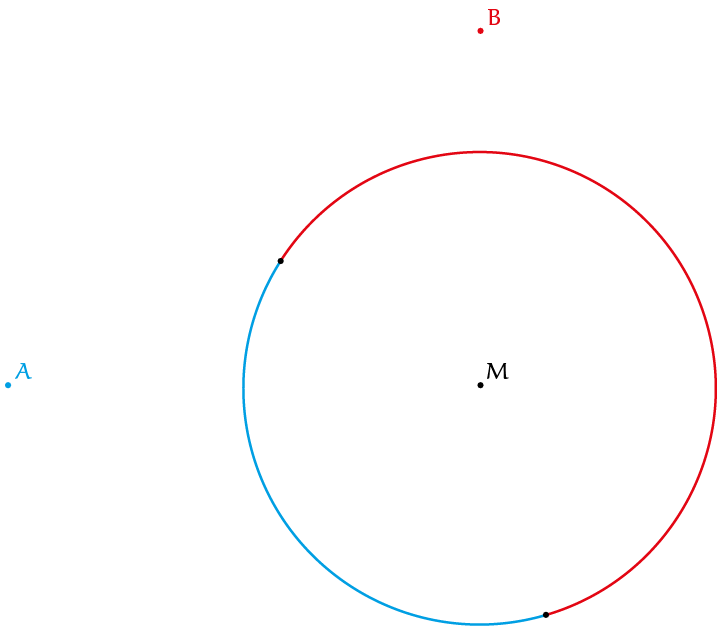
Beschouw een cirkel met middelpunt $M$ en straal $1$. Gegeven zijn punten $A$ en $B$ (niet noodzakelijk op de rand van de cirkel) zodat één derde van de punten op de rand van de cirkel dichter bij $A$ ligt en twee derde dichter bij $B$. Wat is de minimale waarde van $|MA| + |MB|$?

 

 

 

Bekijk oplossing