Opgave 433

Elk neefje moet $10$ muntjes hebben met totale waarde $20$, zodat de gemiddelde waarde van de muntjes gelijk moet zijn aan $2$. De muntjes met waarde $2$ veranderen niets aan dit gemiddelde, zodat de gemiddelde waarde van de muntjes met waarde $1$ en waarde $3$ ook wel $2$ zijn. Met andere woorden, elk neefje heeft evenveel muntjes van waarde $1$ als van waarde $3$. Dit betekent dat we enkel paren van muntjes met waarde $1$ en $3$ onder de neefjes hoeven te verdelen. Er is dan namelijk een unieke manier om de verdeling te completeren met de muntjes van waarde $2$.

Omdat we $10$ paren muntjes van $1$ en $3$ moeten verdelen, moet minstens één van de neefjes wel $4$ of $5$ zulke paren krijgen. Als een neefje $5$ zulke paren krijgt, dan zijn er precies drie manieren om de verdeling af te maken. Namelijk, de andere neefjes krijgen dan ofwel $0$ en $5$ paren respectievelijk, ofwel $1$ en $4$ paren respectievelijk, ofwel $2$ en $3$ paren respectievelijk. Als niemand $5$ zulke 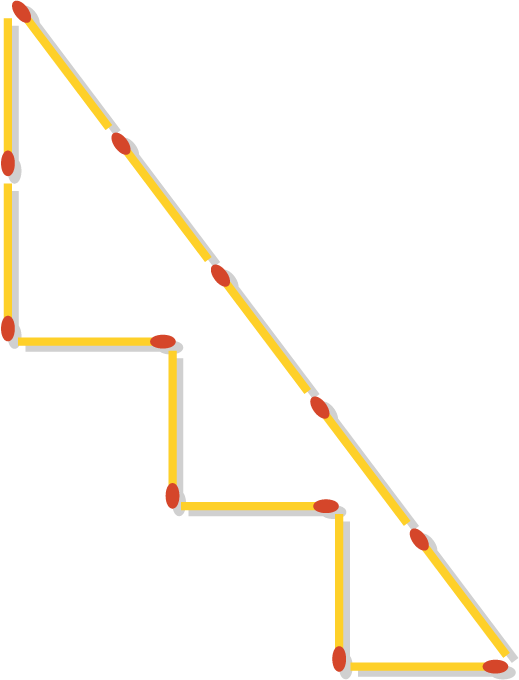paren krijgt, dan kunnen de drie neefjes ofwel respectievelijk $4$, $4$ en $2$ paren krijgen, ofwel $4$, $3$ en $3$. In totaal geeft dit $5$ mogelijke verdelingen.

Opgave 434

Er zijn verschillende manieren om dit vraagstuk op te lossen. Een mogelijke manier is weergegeven in de figuur rechts.

Opgave 435

Als $2/n$ dezelfde decimale expansie heeft als $1/n$, maar dan twee plekken opgeschoven, dan volgt dat $2/n$ en $100/n$ wel precies hetzelfde achter de komma moeten hebben. Namelijk, de decimale schrijfwijze van $100/n$ is gelijk aan die van $1/n$, maar dan met de komma twee plekken opgeschoven. Hieruit volgt dat $(100/n)-(2/n) = 98/n$ alleen maar nullen achter de komma heeft - met andere
woorden, het is een geheel getal. We zien dat $n$ een deler moet zijn van $98$. Omdat $98 = 2 \cdot 7^2$ vinden we snel dat $1$, $2$, $7$, $14$, $49$, $98$ de enige zes delers van $98$ zijn. Technisch gezien voldoen al deze getallen, maar voor $n = 1$ en $n = 2$ is het resultaat enigszins flauw. Het is leuk om met een rekenmachine na te gaan dat $7$, $14$, $49$ en $98$ daadwerkelijk voldoen.

Opgave 436

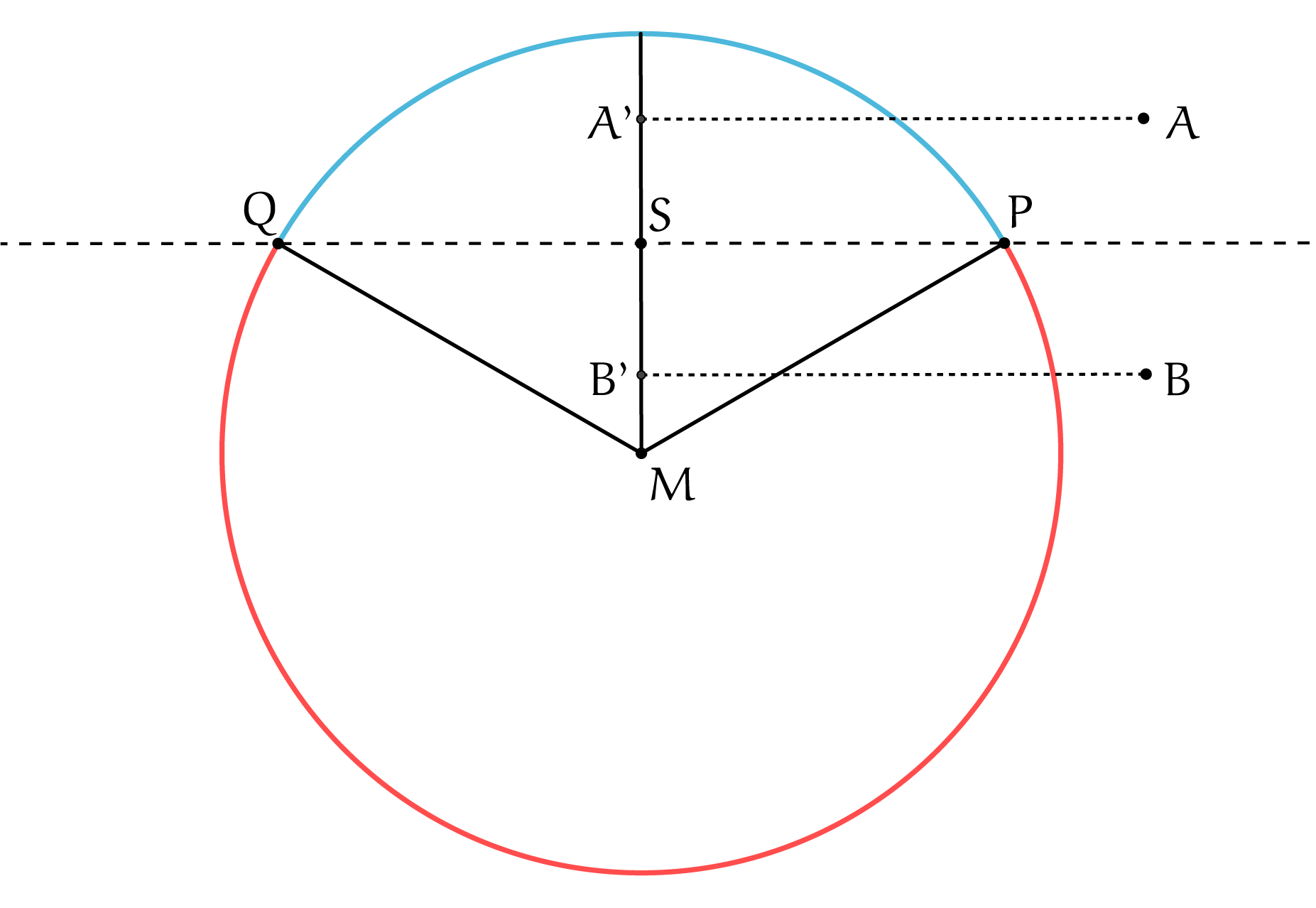
Laat $P$ en $Q$ de snijpunten zijn van de middelloodlijn van $AB$ met de cirkel. Alle punten aan de kant van $A$ van lijn $PQ$ liggen dichterbij $A$ en alle punten aan de kant van $B$ liggen dichterbij $B$. Omdat de punten op de cirkel die dichterbij $A$ liggen precies een derde van de cirkel vormen, zien we dat $\angle PMQ = 360^{\rm o}/3 = 120^{\rm o}$. Zij $S$ de projectie van $M$ op lijnstuk $PQ$. Dan zien we dat $\Delta PSM$ en $\Delta QSM$ beide halve gelijkzijdige driehoeken zijn met lange zijde $1$. Er volgt dat $|SM| = 1/2$.

Merk nu op dat de projecties $A'$ en $B'$ van $A$ en $B$ respectievelijk op de lijn $SM$ dezelfde middelloodlijn $PQ$ hebben als $A$ en $B$. Echter, $|A'M| \le |AM|$ en $|B'M| \le |BM|$, omdat de lange zijde van een rechthoekige driehoek altijd langer is dan de rechthoekszijden. We concluderen dat $A$ en $B$ waarvoor de som $|AM| + |BM|$ minimaal is, wel op lijn $SM$ moeten liggen. Omdat $A$ en $B$ symmetrisch liggen rondom lijn $PQ$, is nu makkelijk in te zien dat die som minimaal is als $A$ en $B$ op het lijnstuk $SM$ liggen, wanneer de som altijd gelijk is aan $1$.