Opgave 489 ^[oOO]

Bepaal alle tweetallen reële getallen $(x, y)$ die voldoen aan de vergelijking $$x+y=\frac{1}{x}+\frac{1}{y}.$$

Opgave 490 ^[oOO]

Beschouw een koordenvierhoek $ABCD$ met $|AB| = |AC|$, $|BC| = |BD|$ en $|AD| = |CD|$. Bepaal de grootte van alle hoeken van de vierhoek.

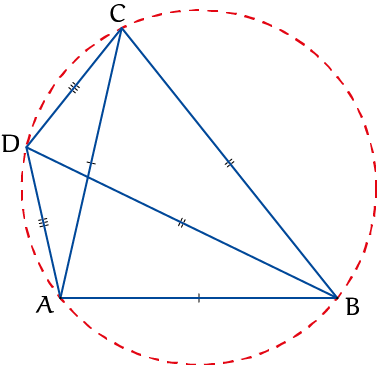
Hint: Als je niet bekend bent met koordenvierhoeken, bekijk eens https://nl.wikipedia.org/wiki/Middelpuntshoek_en_omtrekshoek.

Opgave 491 ^[ooO]

Laat $ABCD$ een convexe vierhoek zijn en veronderstel dat $$\cos(\angle A) + \cos(\angle B) + \cos(\angle C) + \cos(\angle D) = 0.$$

Bewijs dat $ABCD$ een koordenvierhoek of een trapezium is. 

Opgave 492 ^[ooO] 

Beschouw de rij getallen 

$1 \cdot 4 = 4$,
$3 \cdot 6 = 18$,
$5 \cdot 8 = 40$,
$7 \cdot 10 = 70$,
$9 \cdot 12 = 108$,
$\dots$

Bepaal de waarde van 

$$\sqrt{4+\sqrt{18+\sqrt{40+\sqrt{70+\sqrt{108+\dots}}}}}.$$

Bekijk oplossing