Opgave 493 ^[oOO]

Hoeveel tijdstippen op een digitale $24$-uurs klok bevatten het cijfer $2$?

Opgave 494 ^[oOO]

Het woord $REKEN$ beschrijft een vijfcijferig getal als we elk van de vier letters door een cijfer vervangen. Het blijkt dat

$(R + E + K + E + N)^3 = REKEN$.

Wat zijn de waardes van alle letters?

Opgave 495 ^[ooO]

In een klas met $31$ kinderen schrijven alle kinderen vijf positieve gehele getallen op van $1$ tot en met $25$. Bewijs dat er twee kinderen zijn die twee dezelfde getallen hebben opgeschreven.

Bonus: bewijs dat dit met $30$ kinderen niet zo hoeft te zijn.

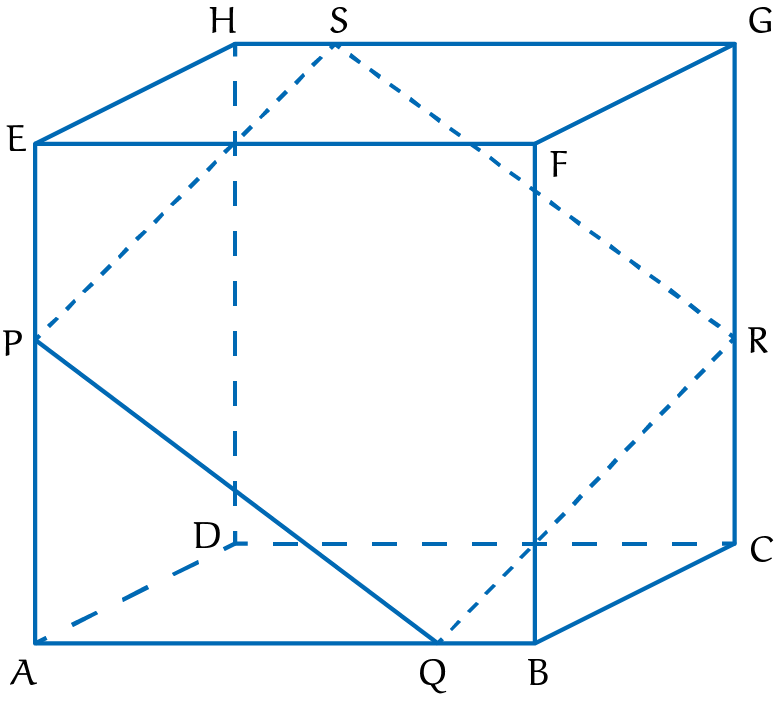
Opgave 496 ^[ooO]

Gegeven de kubus $ABCD\cdot EFGH$ met punten $P$ op $AE$, $Q$ op $AB$, $R$ op $CG$ en $S$ op $GH$ die niet samenvallen met hoekpunten van de kubus. Toon aan dat we die punten zo kunnen kiezen dat $PQRS$ een vierkant is (met dank aan Huub Odijk).

Bekijk oplossing