Opgave 501 ^[oOO]

Bij bushalte Pythagoraslaan was de dienstregeling vroeger zo dat er de hele dag door precies elke $20$ minuten een bus vertrok. Bas keek echter nooit op de klok en verscheen altijd op een willekeurig moment bij de bushalte, waardoor hij gemiddeld $10$ minuten moest wachten totdat de bus er was. De dienstregeling werd echter aangepast: de bussen vertrokken nu altijd op $0$, $10$ en $30$ minuten na het hele uur. Als Bas willekeurig bij de bushalte aan blijft komen, hoe lang is zijn gemiddelde wachttijd dan nu?

Opgave 502 ^[oOO]

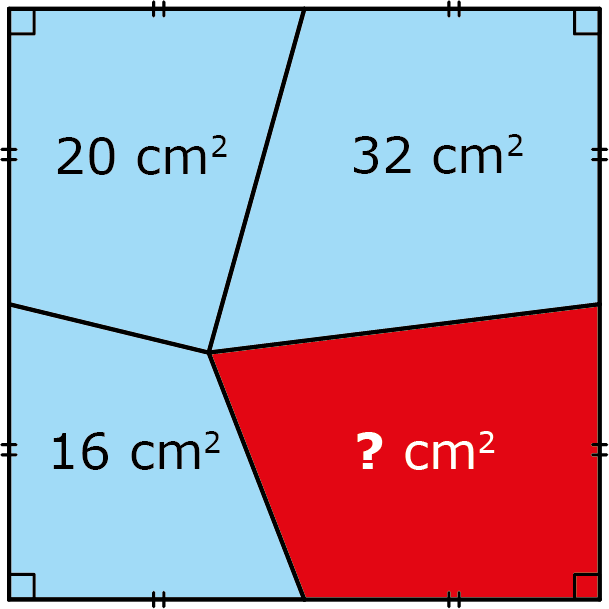
Een vierkant is opgedeeld in vier delen zoals aangegeven in de figuur. De oppervlaktes van drie van deze delen zijn bekend. Wat is de oppervlakte van het vierde gebied?

Opgave 503 ^[ooO]

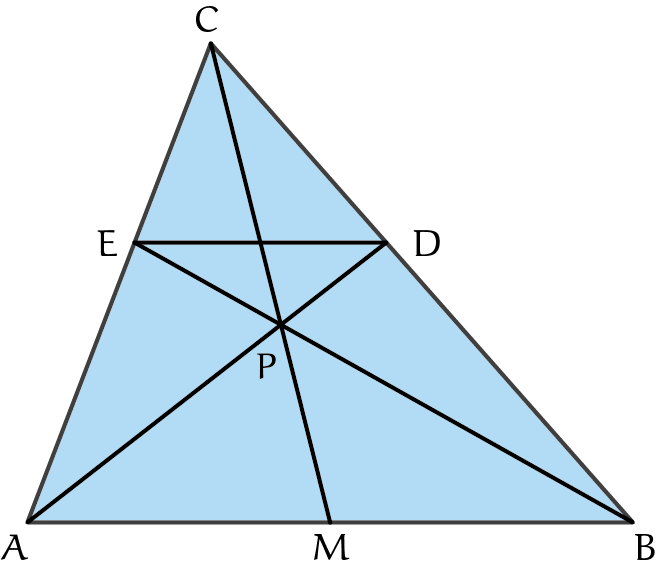
Gegeven is driehoek $ABC$. $M$ is het midden van $AB$, $P$ is een punt op lijnstuk $CM$ en $D$ en $E$ zijn respectievelijk de snijpunten van $AP$ met $BC$ en van $BP$ met $AC$. Bewijs dat $DE$ evenwijdig is aan $AB$.

Opgave 504 ^[ooO]

Bepaal het grootste positieve gehele getal $N$ met de volgende eigenschap: er bestaan $N$ opeenvolgende positieve gehele getallen zodat elk van die getallen deelbaar is door minstens één van de priemgetallen $2$, $3$, $5$, $7$ of $11$.

 

Bekijk oplossing