Opgave 525 ^[oOO]

Anne en Bob hebben onlangs een kindje gekregen. Anne merkt op: "De leeftijd van ons kind in dagen is vandaag een priemgetal." Hierop reageert Bob: "Het zal nog meer dan een week duren voordat dat weer zo zal zijn."

Hoeveel dagen oud is het kindje van Anne en Bob vandaag dan minstens?

Opgave 526 ^[oOO]

Laat $n = 2024^{2024}$. Welk van de getallen $n^{n+1}$ en $(n + 1)^n$ is het grootst?

Opgave 527 ^[ooO]

Van een rij positieve gehele getallen $a_1, a_2,\dots$ definiëren we de verschilrij als de rij $a_2 - a_1, a_3 - a_2,\dots$. Voor een zeker rijtje van positieve gehele getallen $a_1,\dots , a_{20}$ geldt nu dat alle getallen in de verschilrij ook positief zijn, evenals de getallen in de verschilrij van de verschilrij, enzovoorts, tot en met de laatste verschilrij die uit precies één positief geheel getal bestaat.

Wat is dan de kleinst mogelijke waarde van $a_{20}$?

Opgave 528 ^[ooO]

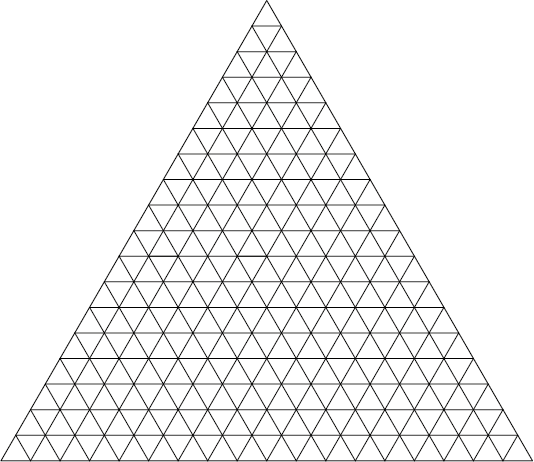
Hieronder is een gelijkzijdige driehoek verdeeld in $18^2 = 324$ even grote kleinere gelijkzijdige driehoekjes. Hoeveel verschillende parallellogrammen zijn er in deze figuur te vinden?

Je inzending moet bij ons binnen zijn vóór 20 september 2024 via [email protected]