Inzenden kan tot 1 november 2026

Opgave 553 ^[oOO]

Jorge heeft drie vier-zijdige dobbelstenen met op elke zijde een letter. Hij dobbelt 8 keer met alle dobbelstenen en probeert dan een woord op te schrijven dat hij kan maken met de letters die hij gerold heeft. Op zijn blaadje staat nu:

$DAL$, $DOR$, $GAT$, $IER$, $ONS$, $RIT$, $RED$, $VEN$.

Welke vier letters stonden er op de drie dobbelstenen?

Opgave 554 ^[oOO]

Anja heeft een getal van 10 cijfers met de eigenschap dat het eerste cijfer gelijk is aan het aantal nullen in het getal, het tweede cijfer gelijk is aan het aantal enen in het getal, enzovoorts, tot en met het tiende cijfer dat gelijk is aan het aantal negens in het getal. Wat is Anja's getal?

Bonuspunt: geef een waterdicht wiskundig bewijs dat er maar één mogelijkheid is - het gebruik van een computer is verboden!

Opgave 555 ^[ooO]

Laat $ABCDEFG$ een regelmatige zevenhoek zijn. De verlengdes van zijden $AG$ en $BC$ snijden in het punt $H$. Bewijs dat $H$ het spiegelbeeld is van het punt $E$ in de lijn $CG$.

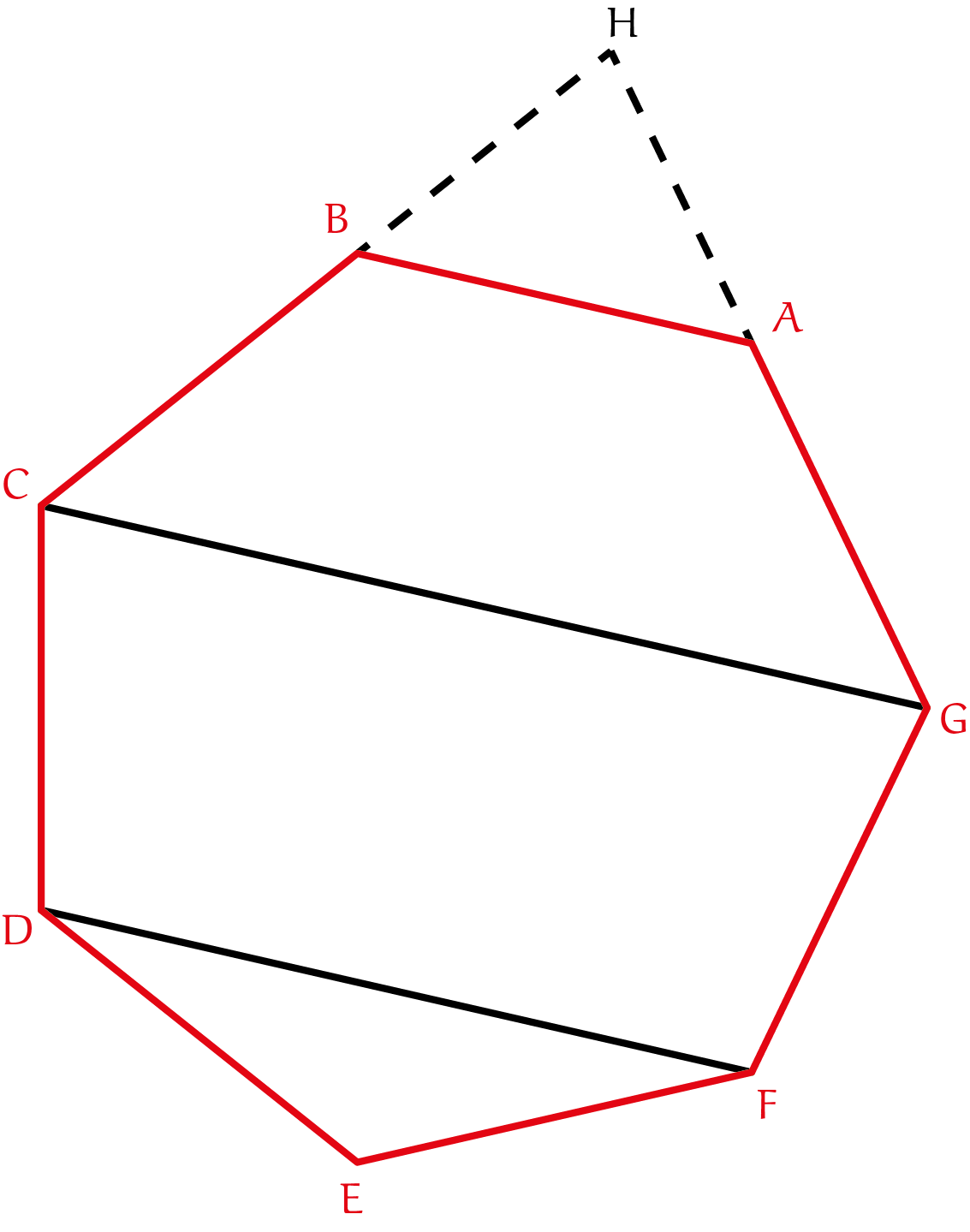
Opgave 556 ^[ooO]

Een aantal positieve gehele getallen is rood gekleurd. De volgende uitspraken blijken te gelden:

• Het getal $1$ is rood gekleurd.
• Als het getal $n$ rood is, dan is $2n$ ook rood.
• Als $n$ en $m$ rood zijn en $n + m$ is even, dan is $(n + m)/2$ ook rood.

Bewijs dat alle positieve gehele getallen rood gekleurd zijn.

 

Inzenden vóór 1 november 2025 via [email protected]