Het valt op dat de meeste leerlingen zich interesseren voor diepe wiskundige vraagstukken. Verder speelt elk jaar bij veel profielwerkstukken het programmeren een belangrijke ondersteunende rol. Soms hebben inzenders moeite om zich te aan te passen aan het vaak op scholen gebruikte format van hypothese, hoofdvraag en deelvragen. Dit kader past vaak niet goed bij een wiskundig profielwerkstuk. Je ziet wel dat de inzenders gebaat zijn bij het goed kunnen structureren van hun onderzoek, maar je zou soms wensen dat er nog een keer een vertaalslag gemaakt wordt om het beter leesbaar te maken. Verder niets dan lof voor de kandidaten, en ook voor hun begeleiders.

De zeven ingezonden werken

Evelien de Wolff van het St Michaelcollege in Zaandam heeft onderzocht of het spel Set altijd uit is te spelen. Dit combinatorische probleem heeft ze statistisch aangepakt. Ze heeft geprogrammeerd in Excel en door middel van iteraties een uitspraak over dit probleem gedaan. Het is knap dit grote project tot een goed einde te brengen. Daarnaast was haar werkstuk een helder verhaal en mooi geïllustreerd.

Loes Peters en Tom Croese van het Elzendaalcollege in Boxmeer hebben een profielwerkstuk geschreven over benaderingen van $\pi$. Zij hebben mooie beschrijvingen gegeven van allerlei manieren om dit te doen. In een hoofdstuk met de humoristische titel Archimedes 2.0 gebruiken ze de benadering van Archimedes van $\pi$, door onderverdeling van de cirkel in steeds kleinere driehoeken, samen met een geschikte Taylorreeks. Verder hebben ze methodes uit de kansrekening toegepast om $\pi$ te schatten.

Tijmen Romijn van het St. Bonifatiuscollege in Utrecht heeft zich in zijn profielwerkstuk gericht op fundamenten van de wiskunde. Zijn doel was het voor een algemeen (geschoold wiskundig) publiek begrijpelijk maken van de onvolledigheidsstellingen van Gödel.  Hij neemt ons een heel eind mee met dit zeer grote onderwerp. Het is knap dat hij zich zo in de materie heeft kunnen inlezen en dit begrijpelijk heeft verwoord.

Anno van Haandel en Bernadet Klein Wassink van het Openbaar Lyceum Zeist schreven profielwerkstuk  over het ontwikkelen van een algoritme dat een knoop in een koord kan versimpelen. Ze hebben het probleem eerst theoretisch ingekaderd en zijn het toen met Java-programma's te lijf gegaan.  De theoretische inkadering is erg ingewikkeld en het is knap hoever de twee auteurs hiermee zijn gekomen. Het profielwerkstuk is mooi geïllustreerd met veel verduidelijkende figuren. Ook is het erg knap dat ze een compleet werkende app hebben geprogrammeerd die knopen kan vereenvoudigen.

De finalisten

Paco Koers en Lukas Dobbelsteen van het Gymnasium Beekvliet in Sint Michielsgestel hebben geprobeerd een optimale strategie voor het spel Black Jack te ontwikkelen. Dat hebben ze eerst gedaan met Excel, met technieken uit de kansberekening en naderhand met Python. De jury waardeerde vooral de navolgbaarheid van het onderzoek. In dit heldere profielwerkstuk is precies duidelijk tot waar het onderzoek resultaten biedt en waar andere onderzoekers er mee verder zouden kunnen gaan. De Pythondemonstratie bij de eindpresentatie op het mathematisch congres in Eindhoven maakte ook indruk: één miljoen spelen werden doorgerekend in een paar seconden.

Sièna van Schaick en Eline Tiemens van het Minkema College Woerden hebben onderzocht hoe je met wiskundige hulpmiddelen een vloeiend aansluitende lijn door meerdere punten kan trekken. De krommen die zij beschrijven staan bekend als Béziercruves. Het werstuk combineerde theorie en praktijk op een organische manier. Ze demonstreren de Bézier-techniek door het logo van hun school met Bézierkrommes te beschrijven.

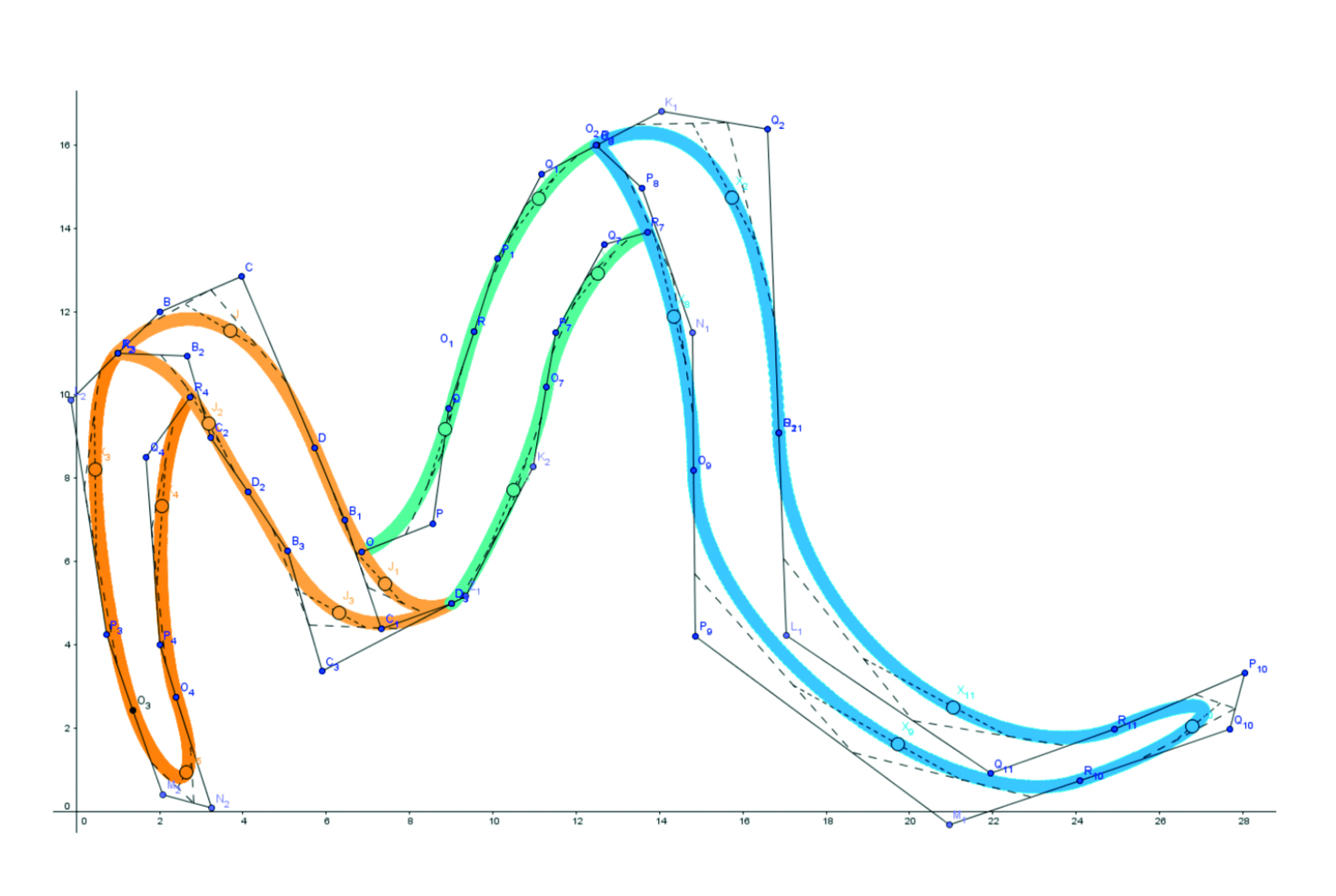
De prachtige animaties in hun presentatie in Eindhoven leverden hen bovendien de publieksprijs 2019 op.

Van geheel andere orde was de beschrijving van de Banach-Tarskiparadox door Joris de Man van het Dominicus College in Nijmegen. Joris de Man heeft de paradox helemaal uitgewerkt met stellingen en bewijzen. Hij heeft dit op een manier gedaan die goed te begrijpen is voor mensen met enige kennis van wiskunde, waarbij wel stevig met groepentheorie en verzamelingen wordt gewerkt.

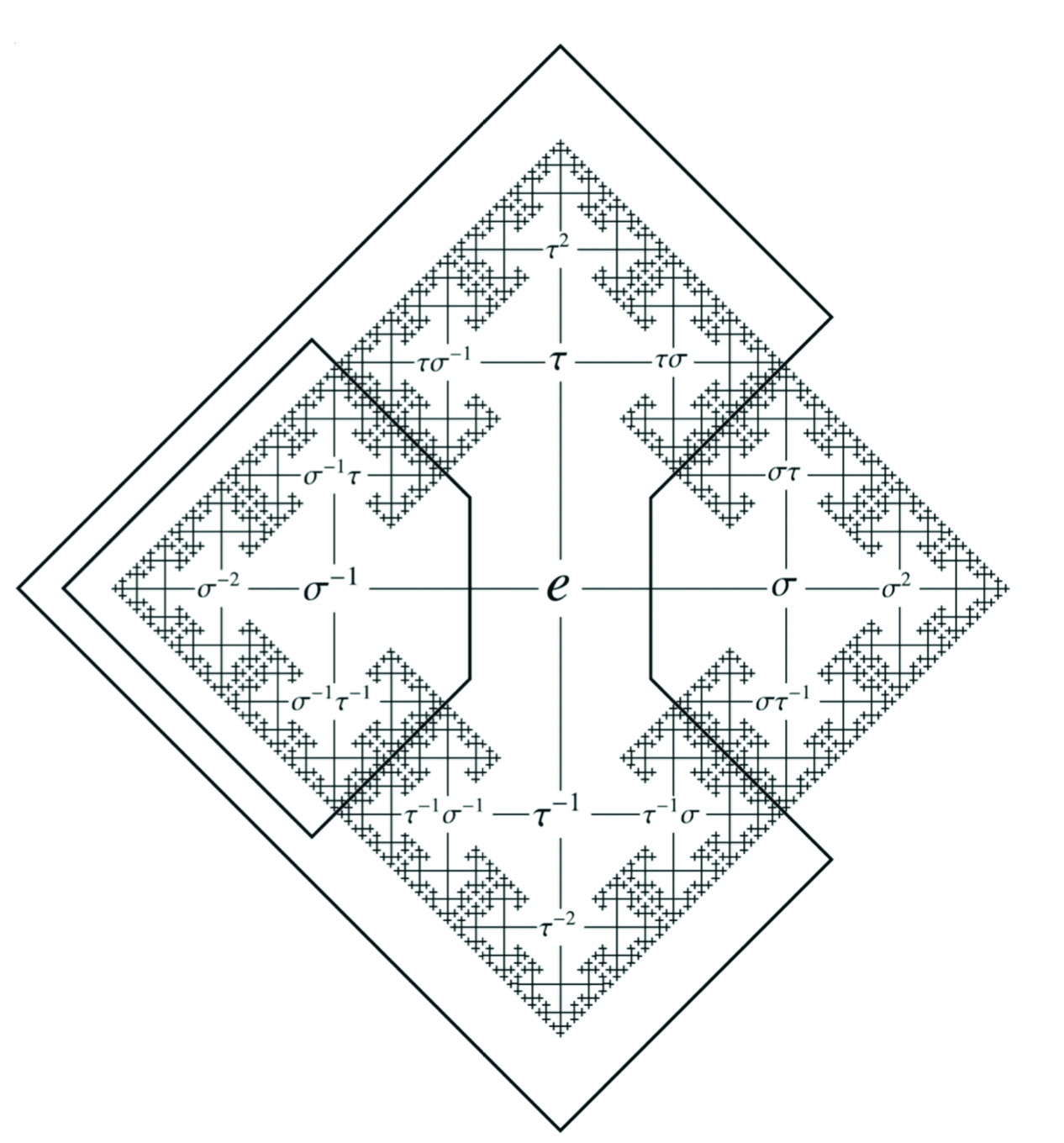
In twee fascinerende hoofdstukken wordt een uitstapje naar de natuurkunde gemaakt. Deze hoofdstukken zijn in grote mate speculatief. Het zou echter flauw zijn om de dwarsverbanden tussen natuurkunde en wiskunde die hij probeert te zien als verzinsels af te doen. Terecht citeert hij met Einstein: ‘Voorzover de stellingen van de wiskunde betrekking hebben op de werkelijkheid zijn ze niet zeker, en voorzover ze zeker zijn betrekken ze zich niet tot de werkelijkheid.’

Eén van de grootste vragen uit de natuurkunde is: hoe goed past het wiskundige model op de werkelijkheid? Wat is werkelijkheid? En wat betekent passend? In een poëtisch laatste deel — De Conclusie — laat Joris de Man zich hier over uit.

Voor deze enorme prestatie krijgt hij de juryprijs. Zijn stuk is ook prachtig geïllustreerd, waardoor je de abstracte begrippen toch steeds goed kan voorstellen.

De profielwerkstukken van de drie finalisten zijn hieronder te downloaden.