01 Sep, 2023
Auteur: Jaap Klouwen
Bladzijde: 22

Pythagorasdoolhof

^[oOO]

Voor doolhofpuzzels zijn de meesten van ons wel wat te oud. Maar wat als je de doorgangetjes weglaat en in plaats daarvan afstanden neerzet? Dan wordt het weer iets voor ons.

Een leuke variant op de bekende 'doolhofpuzzels' is het onderstaande 'getallendoolhof'. Je begint in dit doolhof in het vakje linksonder, met de $3$. Het doel is vakje $F$, rechtsboven ('Finish'). Het getal dat in een vakje staat geeft aan hoe ver je van daaruit kunt bewegen. Je mag horizontaal of verticaal bewegen, naar onder en naar boven, naar links en naar rechts, maar je mag niet diagonaal. Vanuit het startvakje met de $3$ kun je dus bijvoorbeeld drie vakjes naar boven bewegen, naar het vakje met een $2$, daarna twee naar rechts (het vakje met een $4$), enzovoorts.

Opgave 1

Los het getallendoolhof op.

Opgave 2

Verzin zelf zo'n getallendoolhof. Dat mag ook best een kleiner (of zelfs groter) doolhof zijn. Wel vereist is dat er maar één route als oplossing is. Leuke vondsten kunnen worden gepubliceerd in het vijfde deel van de Denkwaar-serie. (Het getallendoolhof stond in het vierde deel, Denkwereld, 2022).

In het doolhof hierboven geven de getallen de horizontale of verticale afstand tussen sommige vakjes aan. Maar waarom zouden we ons beperken tot gehele getallen
van die afstanden in zo'n doolhof? Zo kwam ik op het idee van het 'Pythagorasdoolhof'. Je mag nu soms ook schuin door het doolhof lopen. Er geldt dan een gevolg van de stelling van Pythagoras. De afstand tussen twee van die schuin ten opzichte van elkaar liggende vakjes is de wortel van de kwadratensom van de beide (horizontale en verticale) afstanden: $c = \sqrt{a^2 + b^2}$. Hieronder is zo'n Pythagorasdoolhof gegeven.

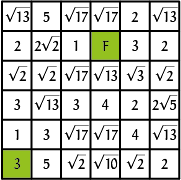
Het startvakje is de $3$ linksonder en het eindvakje is de $F$ (van finish) in de 2^e rij en de 4^e kolom. Je mag dus nu bijvoorbeeld van het vakje in de derde rij vanaf onder en de tweede kolom, met daarin het getal $\sqrt{13}$, naar drie vakjes gaan: die met daarin $\sqrt{17}$ ($2$ opzij, $3$ omhoog), het vakje met een $3$ ($3$ opzij, $2$ omhoog) en het vakje met $\sqrt{2}$ ($3$ opzij, $2$ naar beneden). Alle drie hebben precies de afstand $2^2 + 3^2 = \sqrt{13}$ tot dat beginvakje.