Python-programmatuur bij Functie met je GR onderzoeken
FunCties tekenen in Python
Het tekenen van de functies gebeurt met matplotlib. Dat is vrij technisch. Hieronder worden enkele details uitgelegd die wij gebruiken. Voor andere details moet je kijken op internet.
- Numpy heeft een procedure $linspace$ die een lijst van $x$-waarden genereert, gegeven $X_0$ en $X_1$. De derde variabele is $NP$, het aantal punten dat wordt getekend. Om de Bezier-kromme te tekenen (zie 6. en 7.) wordt dan gebruik gemaakt van een parameterkromme (bewegingsvergelijking).
We hebben hier te maken met een aantal $t$-waarden en drukken $x$ en $y$ uit in $t$. - In elke functie maken we gebruik van $fig = plt.figure(figsize=(6, 6), dpi=150)$. Door de waarde achter $dpi$ aan te passen kun je een plaatje krijgen met hogere of lagere resolutie, belangrijk voor je werkstuk.
- Ook keert $ax = fig.add\_subplot(1, 1, 1)$ altijd terug. In principe kun je verschillende plotten naast en onder elkaar plaatsen. Daarvoor moeten de coördinaten worden aangepast.
- Met $plt.plot(x,y, ‘r’,label=‘y=ln(x)’)$ wordt uiteindelijk de functie getekend. $x, y$ zijn de $x$ en $y$-coördinaat. Daarna volgt de kleur ($‘r’$ staat voor rood, $‘b’$ voor blauw en $‘g’$ voor groen. Tenslotte kan er voor worden gekozen om een $label$ mee te geven. Enkele regels verder op staat $legend$. Hier kun je aangeven waar deze labels worden geplaatst.
- Hierboven werd simpel gebruik gemaakt van $‘r’$ om een kleur weer te geven. Er zijn bijzonder veel benamingen. Los daarvan kun je er ook voor kiezen om zelf een kleur te kiezen uit het RGB-spectrum. De basiskleuren op de computer zijn rood, groen en blauw. Die varieren allen van $0$ tot $1$. $c = (0, 0, 0) $ levert het ontbreken van deze drie kleuren op, dus zwart en $c = (1, 1, 1)$ is wit. Voor $N = 100$ kun je met $c = (i/N, 0, 1-i/N)$ langzaam van rood naar blauw gaan in $100$ stappen.
VersChillen met de GR's van Texas Instruments en Numworks
De grafische rekenmachines hebben een beperkt geheugen en bevatten bij lange na niet alle bibliotheken van Python. Bovendien heeft Texas Instruments (voor de TI-84CE-T Python Editie) een eigen plot-bibliotheek (ti_plotlib) en heeft de plot-bibliotheek van Numworks net wat andere functionaliteit. Bij dat laatste heeft het team van Numworks zelf ons bijgestaan.
Dat betekent dat je de standaard Python-programmatuur op een aantal plaatsen moet aanpassen.
Numpy
Beide GR's kunnen geen gebruik maken van Numpy. Dat betekent dat de procedure $linspace$ niet gebruikt kan worden, en bovendien het werken met arrays iets anders moet. In onderstaande programmatuur betekent dat vooral het volgende.
De constructie
x = linspace(A, B, N)
moet herschreven worden naar
x = [A + i*(B-A)/(N-1) for i in range(N)]
Het werken met een vector $x$ moet dan verder aangepast. In plaats van
x = wiskundige_bewerking(x)
moet je schrijven
x = [wiskundige_bewerking(xi) for xi in x]
Mathplotlib
Om te beginnen heeft de TI dus een eigen plotlib. Dus op de TI schrijf je niet
import mathplotlib.pyplot as plt
maar
import ti_plotlib as plt
Verder zijn er al dan niet subtiele verschillen tussen de plot-bibliotheken.
Op de GR kun je om te beginnen geen figure definiëren met subplots. Ook de assen kun je niet afzonderlijk benaderen.
De kleuren in RGB lopen op een GR van $0$ tot $255$ en niet van $0$ tot $1$ zoals in standaard Python.
Verder moet je op de TI vóór je een punt tekent de kleur instellen, en vervolgens een stip ('.') apart tekenen, met
plt.color(waardeR, waardeG, waardeB) plt.plot(x,y,'.')
terwijl je op de Numworks de kleur als vector invoert:
plt.plot(x,y,[waardeR, waardeG, waardeB])
Bovendien moet je op de TI eerst handmatig het scherm leegmaken en het window handmatig op de juiste dimensies zetten:
plt.cls() plt.window(x_min, x_max, y_min, y_max)
Op dit moment heb ik nog niet goed in de gaten hoe ik alle labels en titels kan toevoegen aan de figuren, evenmin de legenda.
Geheugen
Ten slotte heeft de beperking van het geheugen ook tot gevolg dat je minder punten of lijnen kunt tekenen. In het algemeen zul je de waarde van $NP$ (flink) moeten verlagen, evenals sommige andere waarden. Bij de vulkaan kun je minder paden van lavabommen tekenen.
De programmatuur zelf (standaard Python)
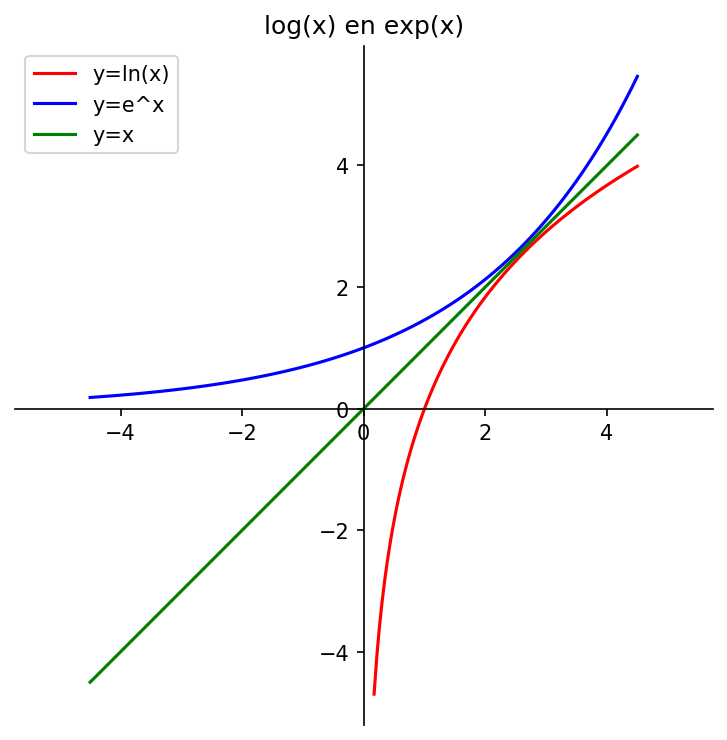
# 4. Natuurlijke logaritme (Opgave 1-3)
import matplotlib.pyplot as plt
import numpy as np
import math
PN = 100
PU = 1/PN
X0 = 17*PU
X1 = 4.5
x1 = np.linspace(X0, X1, PN)
x2 = np.linspace(-X1, X1, PN)
#p = np.exp(1) # Hiermee raken de krommen
p = 2.65 # Hiermee raken de krommen net niet
Titel = 'log(x) en exp(x)'
f1 = p*np.log(x1)
f2 = np.exp(x2/p)
f3 = x2
Xas = 0
Yas = 0
fig = plt.figure(figsize=(6, 6), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
plt.plot(x1,f1, 'r',label='y=ln(x)')
plt.plot(x2,f2, 'b',label='y=e^x')
plt.plot(x2,f3, 'g',label='y=x')
plt.axis('equal')
plt.legend(loc='upper left')
plt.show()
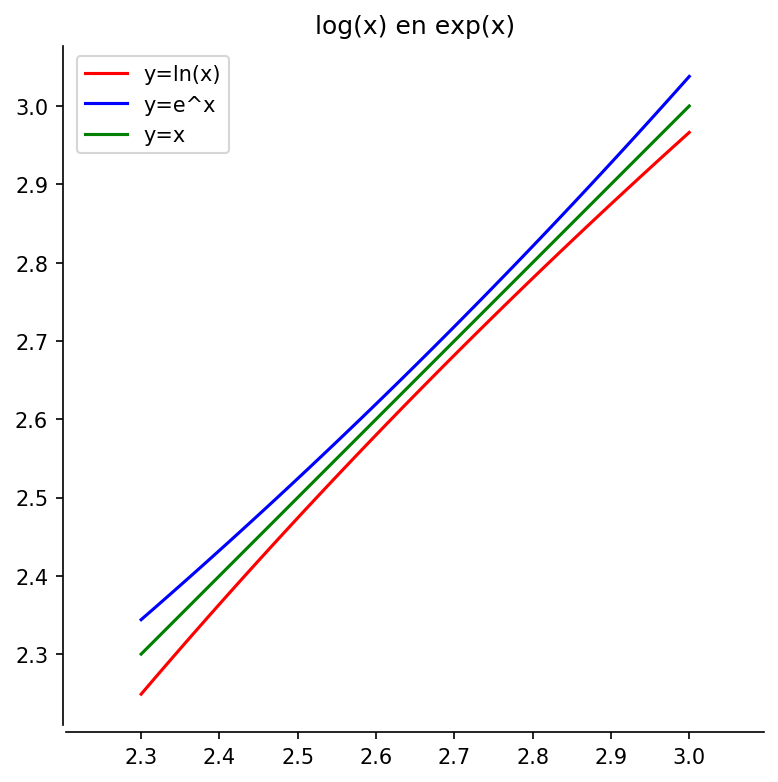
# 5. Natuurlijke logaritme (Opgave 1-3)
# Uitvergroting rondom het raakpunt.
import matplotlib.pyplot as plt
import numpy as np
import math
PN = 100
PU = 1/PN
X0 = 2.3
X1 = 3
x1 = np.linspace(X0, X1, PN)
x2 = np.linspace(X0, X1, PN)
#p = np.exp(1) # Hiermee raken de krommen
p = 2.7 # Hiermee raken de krommen net niet
Titel = 'log(x) en exp(x)'
f1 = p*np.log(x1)
f2 = np.exp(x2/p)
f3 = x2
Xas = X0 - 0.1
Yas = X0 - 0.1
fig = plt.figure(figsize=(6, 6), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
plt.plot(x1,f1, 'r',label='y=ln(x)')
plt.plot(x2,f2, 'b',label='y=e^x')
plt.plot(x2,f3, 'g',label='y=x')
plt.axis('equal')
plt.legend(loc='upper left')
plt.show()
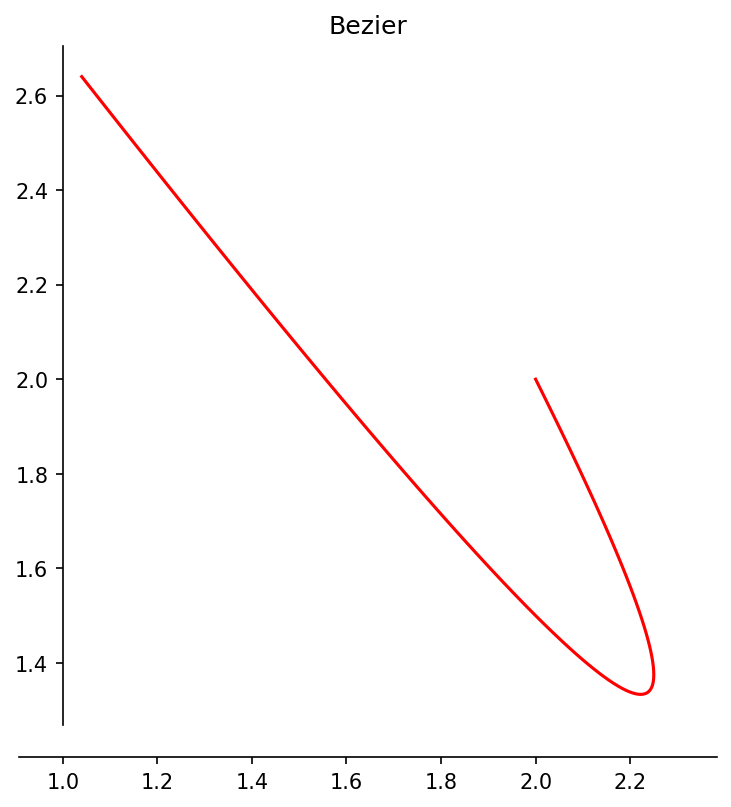
# 6. Bezierkromme (Opgave 7)
# x(t) = -4t^2+6t
# y(t) = 6t^2-8t+4
import matplotlib.pyplot as plt
import numpy as np
import math
PN = 100
T0 = 0.2
T1 = 1
Ax = 0
Ay = 4
Bx = 2
By = 2
Cx = 3
Cy = 0
x = (1-t)**2*Ax + t**2*Bx + 2*t*(1-t)*Cx
y = (1-t)**2*Ay + t**2*By + 2*t*(1-t)*Cy
t = np.linspace(T0, T1, PN)
Titel = 'Bezier'
Xas = 1.2
Yas = 1
fig = plt.figure(figsize=(6, 6), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
plt.plot(x,y, 'r')
plt.axis('equal')
plt.show()
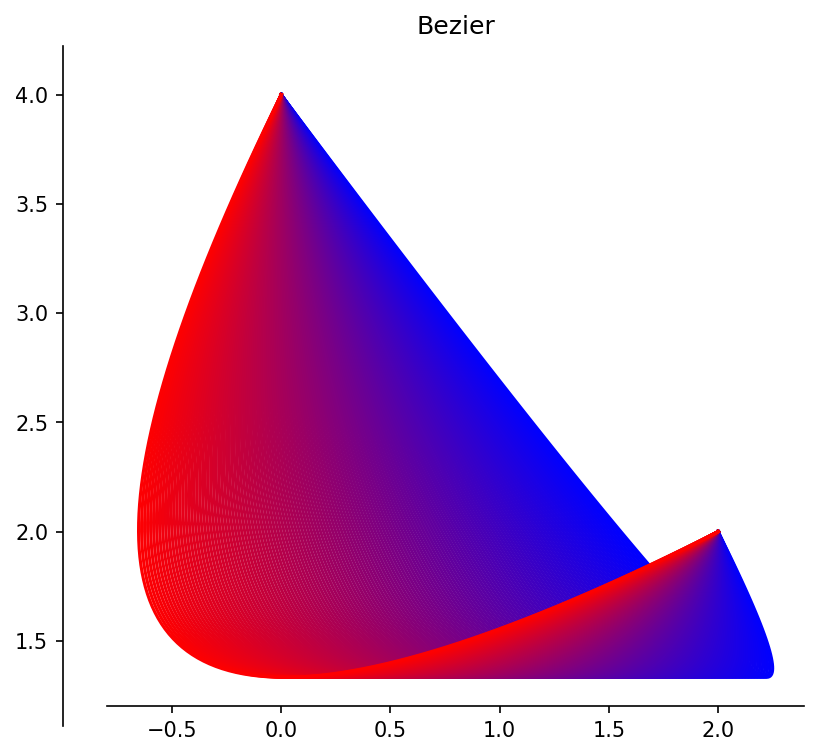
# 7. Bezierkrommem (Opgave 7)
# x(t) = -4t^2+6t
# y(t) = 6t^2-8t+4
# Je kunt zelf eens proberen om het punt C een andere baan te laten beschrijven.
import matplotlib.pyplot as plt
import numpy as np
import math
PN = 100
T0 = 0
T1 = 1
Ax = 0
Ay = 4
Bx = 2
By = 2
t = np.linspace(T0, T1, PN)
Titel = 'Beziers'
Xas = 1.2
Yas = -1
CRange = 160
fig = plt.figure(figsize=(6, 6), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
for i in range(CRange):
Cx = 3 - 5*i/CRange
Cy = 0
x = (1-t)**2*Ax + t**2*Bx + 2*t*(1-t)*Cx
y = (1-t)**2*Ay + t**2*By + 2*t*(1-t)*Cy
plt.plot(x,y, c = (i/CRange, 0, 1-i/CRange))
plt.axis('equal')
plt.show()
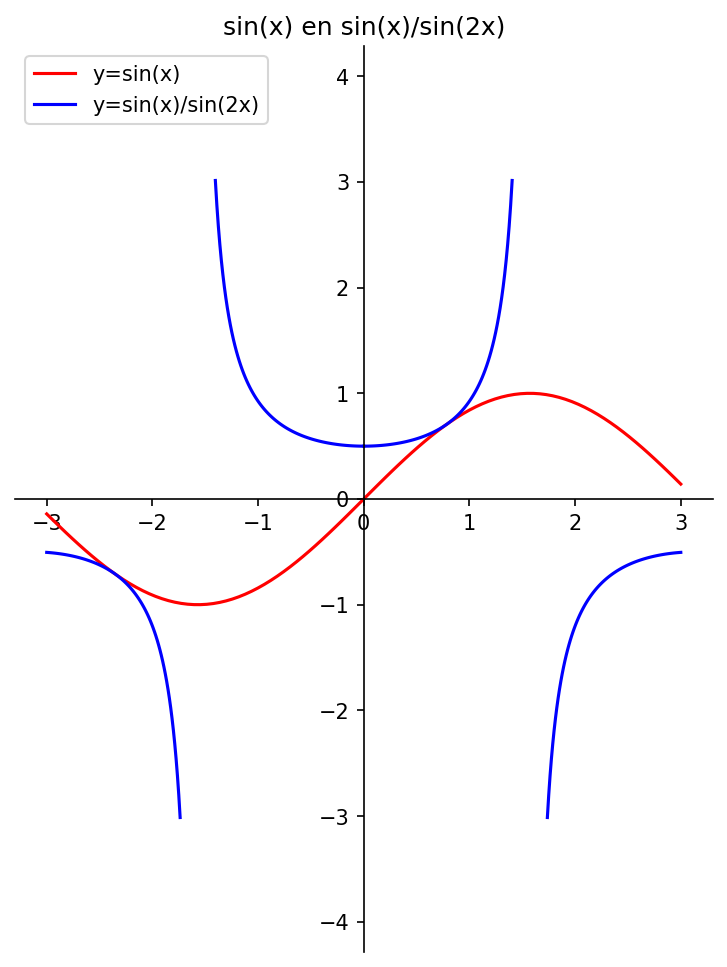
# 8. Gebroken sinuskromme (Opgave 8)
# Let op het was nog wel een gepuzzel om bij de polen (plaatsen waar de functie
# niet bestaat) een gebiedje te definieren waar geen functiewaarden worden
# berekend.
import matplotlib.pyplot as plt
import numpy as np
import math
Pi2 = math.pi/2
PN = 100
PUP = 1/6
PU = 1/1000
X0 = -3
X1 = 3
x1 = np.linspace(X0, X1, PN)
x2 = np.linspace(X0, -Pi2-PUP, PN)
x3 = np.linspace(-Pi2+PUP, -PU, PN)
x4 = np.linspace(PU, Pi2-PUP, PN)
x5 = np.linspace(Pi2+PUP, X1, PN)
Titel = 'sin(x) en sin(x)/sin(2x)'
f1 = np.sin(x1)
f2 = np.sin(x2)/np.sin(2*x2)
f3 = np.sin(x3)/np.sin(2*x3)
f4 = np.sin(x4)/np.sin(2*x4)
f5 = np.sin(x5)/np.sin(2*x5)
Xas = 0
Yas = 0
fig = plt.figure(figsize=(6, 8), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
#plt.plot(range(5))
plt.plot(x1,f1, 'r',label='y=sin(x)')
plt.plot(x2,f2, 'b',label='y=sin(x)/sin(2x)')
plt.plot(x3,f3, 'b')
plt.plot(x4,f4, 'b')
plt.plot(x5,f5, 'b')
plt.axis('equal')
plt.legend(loc='upper left')
plt.show()
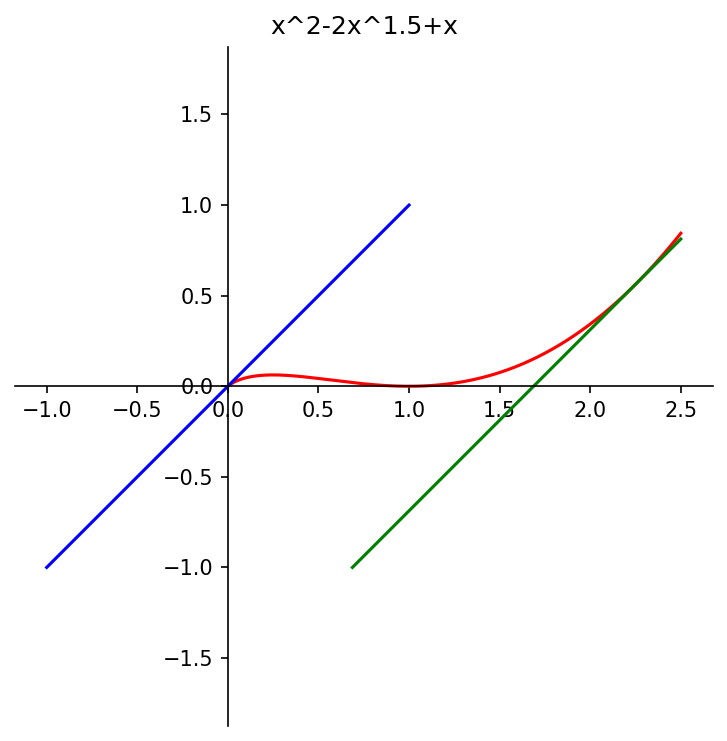
# 9. Evenwijdige raaklijnen. Opgave 9 - 11
# De berekening die ten grondslag ligt voor de tekening is hier niet
# terug te vinden. Kijk daarvoor bij de uitwerkingen van het eindexamen.
import matplotlib.pyplot as plt
import numpy as np
import math
PN = 1000
PU = 1/PN
X0 = 0
X1 = 2.5
x = np.linspace(X0, X1, PN)
x2 = np.linspace(-1, X1-1.5, PN)
x3 = np.linspace(11/16, X1, PN)
Titel = 'x^2-2x^1.5+x'
f = x*x+x-2*x*np.sqrt(x)
g = x2
h = x3-27/16
Xas = X0
Yas = X0
fig = plt.figure(figsize=(6, 6), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
plt.plot(x,f, 'r')
plt.plot(x2,g, 'b')
plt.plot(x3,h, 'g')
plt.axis('equal')
#plt.legend(loc='upper center')
plt.show()
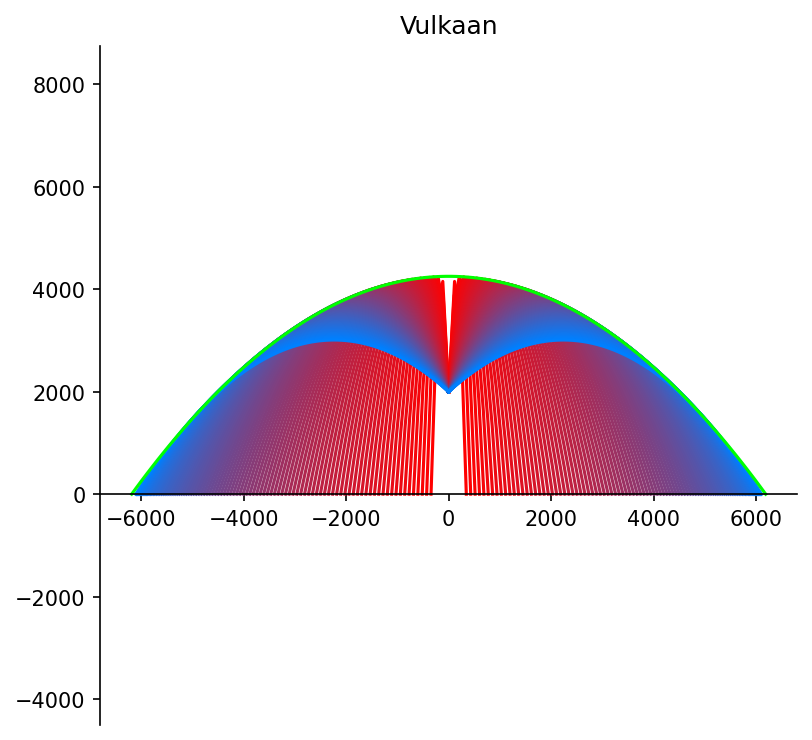
# 10. Vulkaan, Opgave 12 - 14
# ta = tan(alpha)
# y = -(1 + ta^2)/x^2*9000 + ta*x + 2000
#
# Hier zijn in een tekening meerdere functies met varierende alpha
# getekend.
import matplotlib.pyplot as plt
import numpy as np
import math
Pi = math.pi
Titel = 'Vulkaan'
fig = plt.figure(figsize=(6, 6), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
RNG = 100
BND = 3.9
RST = 1/2-1/BND
XX = 9000 * 4250
X = math.sqrt(XX)
for ii in range(RNG+1):
i = RNG-ii
alpha = (1/(BND*RNG) * (i-4) + RST) * Pi
ta = math.tan(alpha)
a = -(1 + ta**2)/9000
b = ta
c = 2000
disc = b*b - 4*a*c
worteldisc = math.sqrt(disc)
X0 = (-b+worteldisc)/(2*a)
X1 = (-b-worteldisc)/(2*a)
PN = round((X1-X0)/100)
xm = np.linspace(-X1, 0, PN)
fm = a*xm**2 - b*xm + c
plt.plot(xm, fm, c = (i/RNG, 0.5-i/(2*RNG), 1-i/RNG))
xp = np.linspace(0, X1, PN)
fp = a*xp**2 + b*xp + c
plt.plot(xp,fp, c = (i/RNG, 0.5-i/(2*RNG), 1-i/RNG))
PN = round(X/50)
x = np.linspace(-X, X, PN)
f = -x**2/9000 + 4250
plt.plot(x,f, c = (0,1,0))
Xas = 0
Yas = -7000
#Yas = 0
plt.axis('equal')
#plt.legend(loc='upper center')
plt.show()
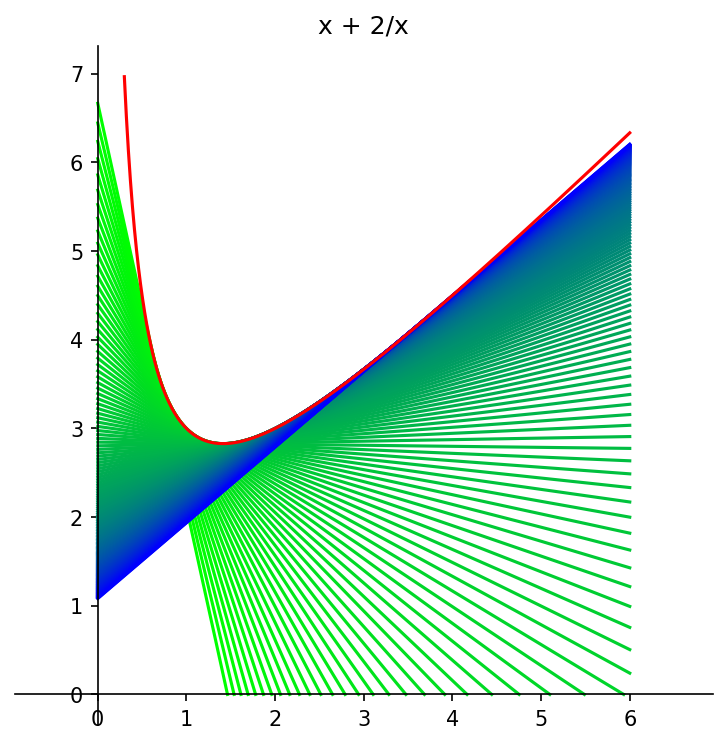
# 11. Scheve asymptoot, Opgave 15
import matplotlib.pyplot as plt
import numpy as np
import math
Titel = 'x + 2/x'
Xas = 0
Yas = 0
fig = plt.figure(figsize=(6, 6), dpi=150)
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position(('data',Yas))
ax.spines['bottom'].set_position(('data',Xas))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title(Titel)
PN = 500
PU = 1/PN
X0 = 0.3
X1 = 6
p0 = 0.6
p1 = 3.7
RNG = 150
X0 = 0
# g = x
# x = np.linspace(X0, X1, PN)
# plt.plot(x,g, 'b',label='y=x')
for i in range(RNG+1):
p = p0 + i*(p1-p0)/RNG
fp = p + 2/p
rcp = 1-2/p**2
cnt = fp - p*rcp
X2 = -cnt/rcp
if rcp < 0:
XX0 = X0
XX1 = min(X1,X2)
else:
XX0 = max(X0,X2)
XX1 = X1
x = np.linspace(XX0, XX1, PN)
h = rcp*x + cnt
plt.plot(x,h, c = (0, 1-i/RNG, i/RNG))
X0 = 0.3
X1 = 6
x = np.linspace(X0, X1, PN)
f = x + 2/x
plt.plot(x,f, 'r')
# plt.legend(loc='upper center')
plt.axis('equal')
plt.show()