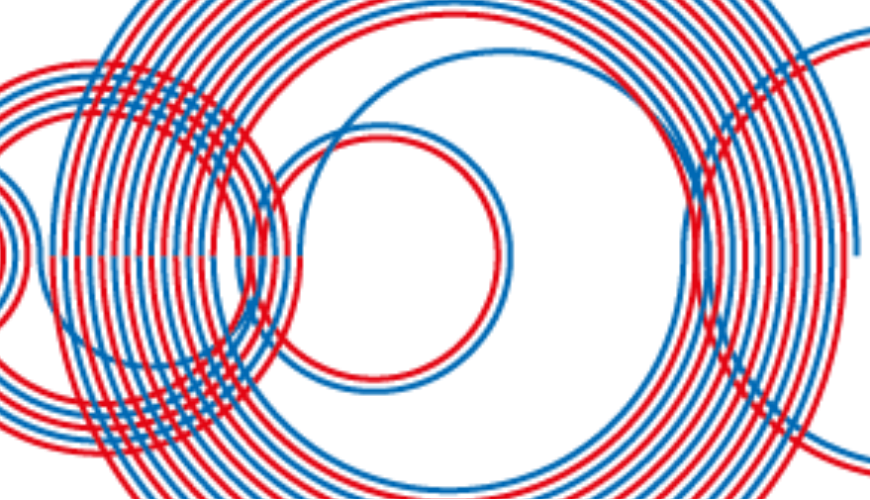
Recamán
[ooO]
Sommige schijnbaar simpele recepten leiden tot gecompliceerde (en met behulp van Python mooie) resultaten.
Bernardo Recamán Santos is de naamgever van een rij getallen met de volgende beschrijving. Ga uit van het getal $0$ en probeer achtereenvolgens de getallen $1, 2, 3, \dots$ er van af te trekken, tenzij je eindigt op een negatief getal of op een getal dat je al eerder hebt gebruikt, in dat geval tel je het betreffende getal op.
Laten we meteen beginnen: $0$. Als je nu $1$ ervan aftrekt dan eindig je negatief, dus tel je $1$ op en kom je uit op $1$. Je gaat door met $2$. $1 - 2 \le 0$. Dus tel je $2$ op en kom je uit op $3$. Vervolgens is $3$ aan de beurt. $3 - 3 = 0$. Maar dat getal komt al in de rij voor. Dus opnieuw tel je $3$ op. De rij die we zo krijgen is $0, 1, 3, 6$. Daarna volgen $2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25$. En zo kun je door blijven gaan.
Het is niet zo dat elk getal in deze rij eenmaal voorkomt. Je zult zien dat $42$ en $43$ tweemaal voor zullen komen. Dat komt doordat er geen restricties zijn in het geval je optelt. Als je uitkomt op een getal dat al voorkomt, dan komt een getal tweemaal (of zelfs vaker) voor.
In de recreatieve wiskunde is dit een hele bekende rij. Waarom? Dat komt door wat Alex Bellos bedacht: de rij getallen zet je niet op een rij, maar je tekent in twee dimensies halve cirkels om van het ene getal naar het volgende getal te gaan. De middellijn van de opeenvolgende cirkels neemt steeds $1$ toe. De halve cirkels teken je wisselend in de bovenhelft en onderhelft. Er ontstaat een prachtige figuur.
De tekening horende bij de eerste $17$ getallen ziet er uit als in figuur 1. Een variant met kleuren geeft de eerste $65$ getallen zoals in figuur 2.
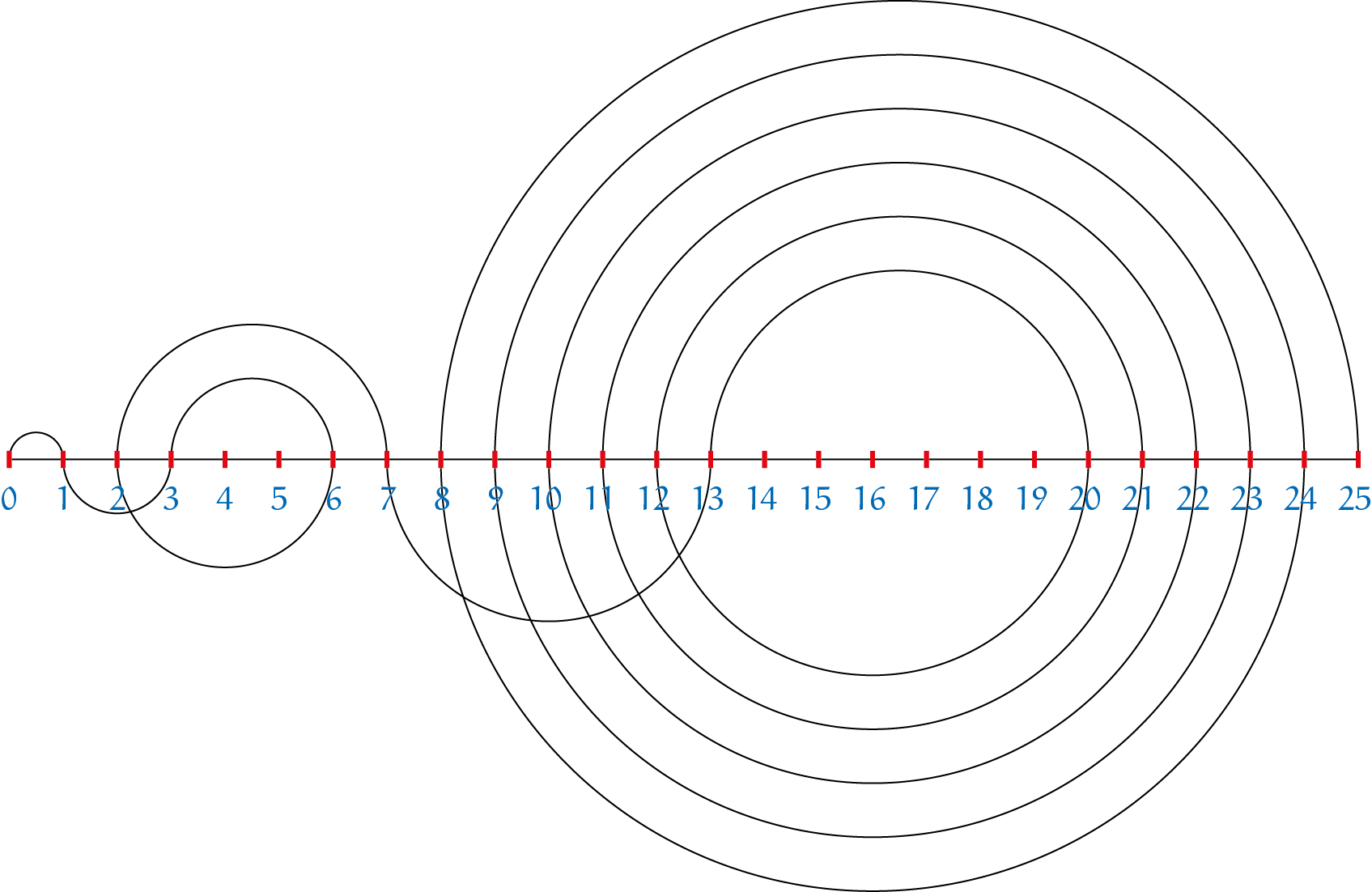
De echte wiskundige vraagt zich af of elk getal in deze rij voorkomt. Dat blijkt helemaal geen vanzelfsprekende vraag. Je kunt de computer er flink op los laten gaan. Het getal $852\,655$ komt voorlopig niet voor, ook al zijn reeds de eerste $10^{230}$ termen berekend.

Opgave 1Probeer zelf het programma voor Recamán te schrijven. Als je er niet uitkomt, dan zie je de rij terug op onze website.
Opgave 2Eerder was al genoemd dat $42$ en $43$ tweemaal voorkomen. Sommige getallen komen zelfs vaker dan tweemaal voor. Welk getal komt als eerste driemaal voor?
Opgave 3*Kun je een rij programmeren zodat herhalingen als $42$ en $43$ helemaal niet voorkomen? |
| Zie ook OEIS: A005132 | ||||
Via [Bekijk oplossing] kom je bij de code.
Bekijk oplossing