In de speciale relativiteitstheorie gaat het over coördinatenstelsels die ten opzichte van elkaar bewegen met constante snelheden. We hebben dan een waarnemer in één stelsel en een in een ander, dat beweegt ten opzichte van het ene.

Laten we eerst deze twee stelsels bekijken in de klassieke theorie. In stelsel $S$ wordt een gebeurtenis vastgelegd door vier coördinaten: $(x, y, z, t)$. In het tweede stelsel $S’$ wordt een gebeurtenis vastgelegd door $(x’, y’, z’, t’)$. $S’$ beweegt met een constante snelheid $v$ in de positieve $x$-richting ten opzichte van $S$. We laten de $x$-assen samenvallen en kiezen voor $t$ en $t’$, als de oorsprongen $O$ en $O’$ met elkaar samenvallen: $t = 0$ en $t’ = 0$. Op dat tijdstip laten we de twee $y$-assen en de twee $z$-assen samenvallen.

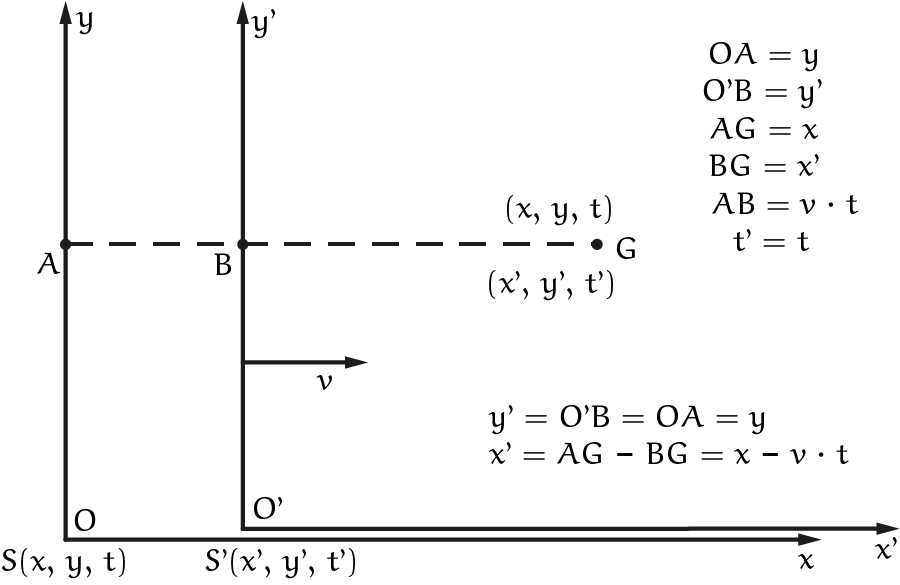
Figuur 1

We nemen nu een gebeurtenis $G$ met coördinaten $(x, y, z, t)$ in stelsel $S$ en $(x’, y’, z’, t’)$ in $S’$. In ieder geval hebben we, zoals we in figuur 1 kunnen zien: 

$$y’ = y.$$

Niet te zien in de figuur, maar om dezelfde reden waarom $y’ = y$, geldt $z’ = z$. Verder geldt in de klassieke theorie natuurlijk $t’ = t$.

Dus:

$$z’ = z\\t’ = t.$$

Voor het verband tussen $x’$ en $x$ geldt, zoals te zien is in figuur 1:

$$x’ = x – vt.$$

Voor de duidelijkheid zijn in figuur 1 de $x$-as en de $x’$-as iets boven elkaar getekend.

Een bijzondere klok in stelsel $S’$

Vanaf nu laten we de coördinaten $z$ en $z’$ weg, omdat toch steeds $z = z’$. Om de consequenties van de constante lichtsnelheid voor elke waarnemer te kunnen verwerken in onze beschouwing, nemen we in stelsel $S’$ een bijzondere klok: we zetten in de oorsprong $O’ = (0, 0)$ en op een hoogte $a$ in $(0, a)$ twee spiegeltjes neer. Zie figuur 2.

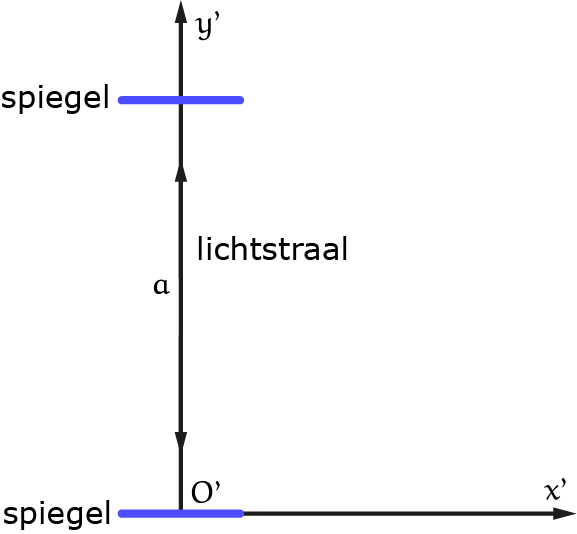
Figuur 2

Tussen deze twee spiegeltjes laten we een lichtstraal steeds heen en weer kaatsen. We laten de straal starten in $O’$ op $t’ = 0$. Dan is de lichtstraal op tijdstip $t’ = 2a/c$ weer terug in $O’$. En zo verder. Dan heeft het stelsel $S’$ in de oorsprong $O’$ een regelmatig 'tikkende’ klok. 

Maar nu willen we weten hoe een waarnemer in $S$ het verschil in tijd tussen de tijdstippen $0$ en $2a/c$ in $S’$ waarneemt. De lichtstraal beweegt voor een waarnemer in $S’$ gewoon op en neer. Maar omdat $S’$ naar rechts beweegt ten opzichte van $S$, beweegt de lichtstraal in $S$ eerst naar rechtsboven, weerkaatst daar, en beweegt daarna naar rechtsonder om weer op het onderste spiegeltje te komen. Zie figuur 3.

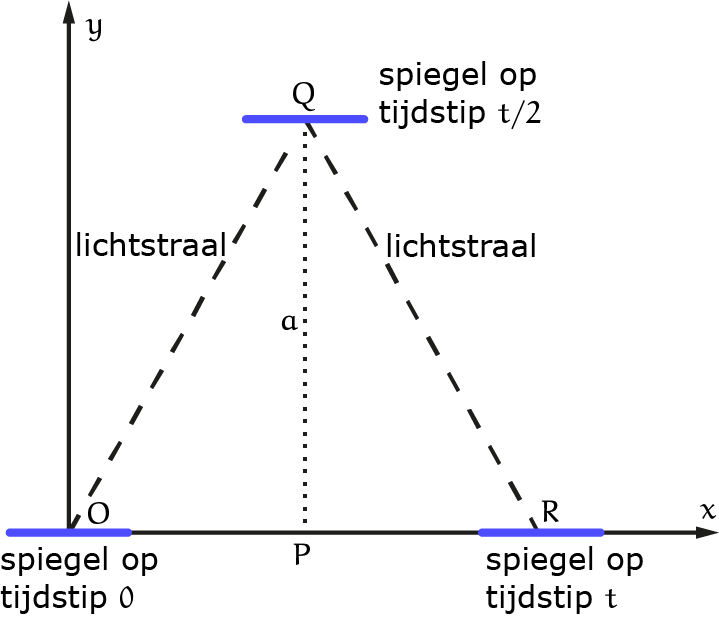
Figuur 3

We bekijken nu in figuur 3 de rechthoekige driehoek $OPQ$. We weten dat $PQ = a$. Verder weten we dat in $S’$ de tijd om heen en weer te gaan $t’$ is. De tijd om alleen naar boven te gaan is dus $t’/2$. Dus: 

$$PQ=\frac{ct'}{2}.$$

In het stelsel $S$ is de tijd dat de lichtstraal heen en weer gaat $t$ (die moeten we berekenen). Dan is de tijd, gemeten in $S$, waarin de lichtstraal van $O$ naar $Q$ gaat $t/2$.

Nu bekijken we $OP$. Het stelsel $S’$ beweegt met een snelheid $v$ naar rechts. In $t/2$ passeert $O’$ punt $P$. Dus:

$$OP =\frac{vt}{2}.$$

Maar nu de schuine zijde $OQ$. In $S$ doet de lichtstraal er een tijd $t/2$ over om $Q$ te bereiken. Maar, nu komt het belangrijkste: deze lichtstraal wordt volgens de relativiteitstheorie in $S$ waargenomen met een snelheid $c$.

Dus:

$$OQ = \frac{ct}{2}.$$

Ten slotte maken we gebruik van de Stelling van Pythagoras: 

$$OP^2 + PQ^2 = OQ^2.$$

		opgave Leid hieruit af dat: $$t=\frac{t'}{\sqrt{1-\frac{v^2}{c^2}}}$$

Tijddilatatie en langzamer lopende klokken

Nu moeten we goed kijken naar de laatste formule. In de eerste plaats zien we aan de wortelvorm in het rechterlid dat die alleen betekenis heeft, als $v < c$. Een materieel voorwerp kan alleen bewegen met een snelheid die kleiner is dan de lichtsnelheid. Alleen een lichtstraal (of lichtdeeltje of foton) plant zich voort met de snelheid $c$.

In de tweede plaats concluderen we uit het feit dat de noemer in het rechterlid kleiner is dan $1$, dat $t > t’$. Als een waarnemer in $S’$ op zijn klok in $S’$ bijvoorbeeld $1$ seconde afleest tussen twee gebeurtenissen, dan leest een waarnemer in $S$ dus een tijd van meer dan $1$ seconde af tussen diezelfde gebeurtenissen. In zijn ogen is er dus sprake van tijddilatatie, een vergroting van de tijd.

Waarnemen van tijddilatatie met atoomklokken

In 1971 stuurden twee Amerikaanse fysici, J.C. Hafele en R.E. Keating een atoomklok mee met een lijnvliegtuig dat twee keer rond de aarde vloog. Bij de start was deze klok gesynchroniseerd met een identieke klok, die op aarde achterbleef. Bij terugkomst en vergelijking van de twee klokken bleek inderdaad dat de gemeten tijd op aarde $t_A$ groter was dan de gemeten tijd in het vliegtuig $t_V$. Dat de algemene relativiteitstheorie hierin ook een factor
was, vanwege de gravitatie, laten we hier onbesproken. 

Muonen bereiken de aarde

De aarde wordt veel gebombardeerd door snelle en zware elementaire deeltjes uit de ruimte. Als ze de dampkring inkomen, botsen ze, naarmate de dampkring wat dichter is, veel tegen kernen van de moleculen in de dampkring. Daarbij komen veel muonen vrij, deeltjes (ruim $200$ keer zo zwaar als een elektron, ongeveer $10$ keer zo licht als een proton) die met grote snelheid $v$ richting aarde bewegen: $v = 0{,}9995c = 0{,}9995 \cdot 3 \cdot 10^8 = 2{,}9985 ⋅ 10^8$ meter per
seconde, dus bijna de lichtsnelheid. Ze ontstaan vrijwel allemaal op een hoogte $h$ van ruwweg $60$ kilometer boven het aardoppervlak. Muonen zijn echter niet stabiel en vervallen in twee andere deeltjes: elektronen en neutrino’s. Daarbij vervalt ongeveer de helft in de halfwaardetijd $t_{\frac{1}{2}}$ van $1{,}5 \cdot 10^{-6}$ seconde. Na die tijd is er dus nog de helft over, na nog een keer de halfwaardetijd nog maar een kwart, enzovoort. 

We bekijken het weer eerst even klassiek. Met een snelheid $v$ bereikt een muon dat niet vervalt in $t_a = h/v = 60\,000/(0{,}9995\cdot 3 \cdot 10^8) = 2 \cdot 10^{-4}$ seconde de aarde. Dat is $t_a/t_{\frac{1}{2}} = 2 \cdot 10^{-4}/1{,}5 \cdot 10^{-6} = 133$ keer de halfwaardetijd. De kans dat een muon zo lang niet zal vervallen is dus $(\frac{1}{2})^{133}$ of ongeveer $1$ op $10^{40}$. De kans dat een muon de aarde haalt is dus vrijwel nul. Hoeveelheden van meer dan $10^{40}$ muonen worden bij lange na niet geproduceerd.

Maar laten we de zaak, zoals het hoort, nu weer relativistisch bekijken. De halfwaardetijd van een muon $t_{\frac{1}{2}}$ is een soort van interne klok in het muon zelf. Een waarnemer op aarde zal deze halfwaardetijd groter meten: $t_{\frac{1}{2}a}$: 

$$t_{\frac{1}{2}a} = \frac{t_{\frac{1}{2}}}{\sqrt{1-\frac{v^2}{c^2}}} = \frac{1{,}5\cdot10^{-6}}{\sqrt{1-\frac{(2{,}9985\cdot 10^8)^2}{(3\cdot 10^8)^2}}} = 4{,}7 \cdot 10^{-5}.$$

In die tijd legt een muon dat niet vervalt een afstand af van $4{,}7 \cdot 10^{-5} \cdot 2{,}9985 \cdot 10^8 = 1{,}4 \cdot 10^4$ meter = $14$ kilometer. Op weg naar de aarde vanaf een hoogte van 60 kilometer, dat is ruim vier keer de afstand
van $14$ kilometer, is de kans dat een muon de aarde bereikt en gemeten kan worden dus iets kleiner dan $(\frac{1}{2})^4 = \frac{1}{16}$. Er worden zeker zoveel muonen geproduceerd om er veel op aarde te kunnen meten. Hier geeft de relativistische berekening en het waarnemen van veel muonen op aarde dus een sterke aanwijzing dat de relativistisch theorie hier juist is.

Relativiteitstheorie deel 3

In de volgende aflevering leiden we weer enkele bijzondere conclusies uit de speciale relativiteitstheorie af: 

• Gelijktijdige gebeurtenissen in het ene stelsel zijn niet gelijktijdig in een ander stelsel.
• De lengtecontractie: als een staaf met lengte $l$ op de $x$-as van stelsel $S’$ wordt waargenomen in stelsel $S$, dan is de waargenomen lengte in $S$ kleiner dan $l$.

 

Relativiteitstheorie Deel 1: Elke waarnemer meet in alle gevallen dezelfde lichtsnelheid Deel 2: Tijddilatatie en trager lopende klokken Deel 3: Gelijktijdigheid en lengtecontractie Deel 4: De som van twee snelheden Deel 5: Bijzondere gekkigheden