
Relativiteitstheorie - Deel 5
BijzondEre geKkiGhEden
In de vorige artikelen hebben we een aantal aspecten van de relativiteitstheorie besproken. In dit slotartikel van de reeks zullen we een paar gekke bijzonderheden bekijken. Wat gebeurt er als een vliegende stok een schuur via voor- en achterdeur passeert en hoe lijkt een kubus eruit te zien als die boven je hoofd voorbijraast? We maken hierbij gebruik van de ontdekkingen uit de vorige vier delen.
VliEgende stok vliegt doOr eEn schuUr
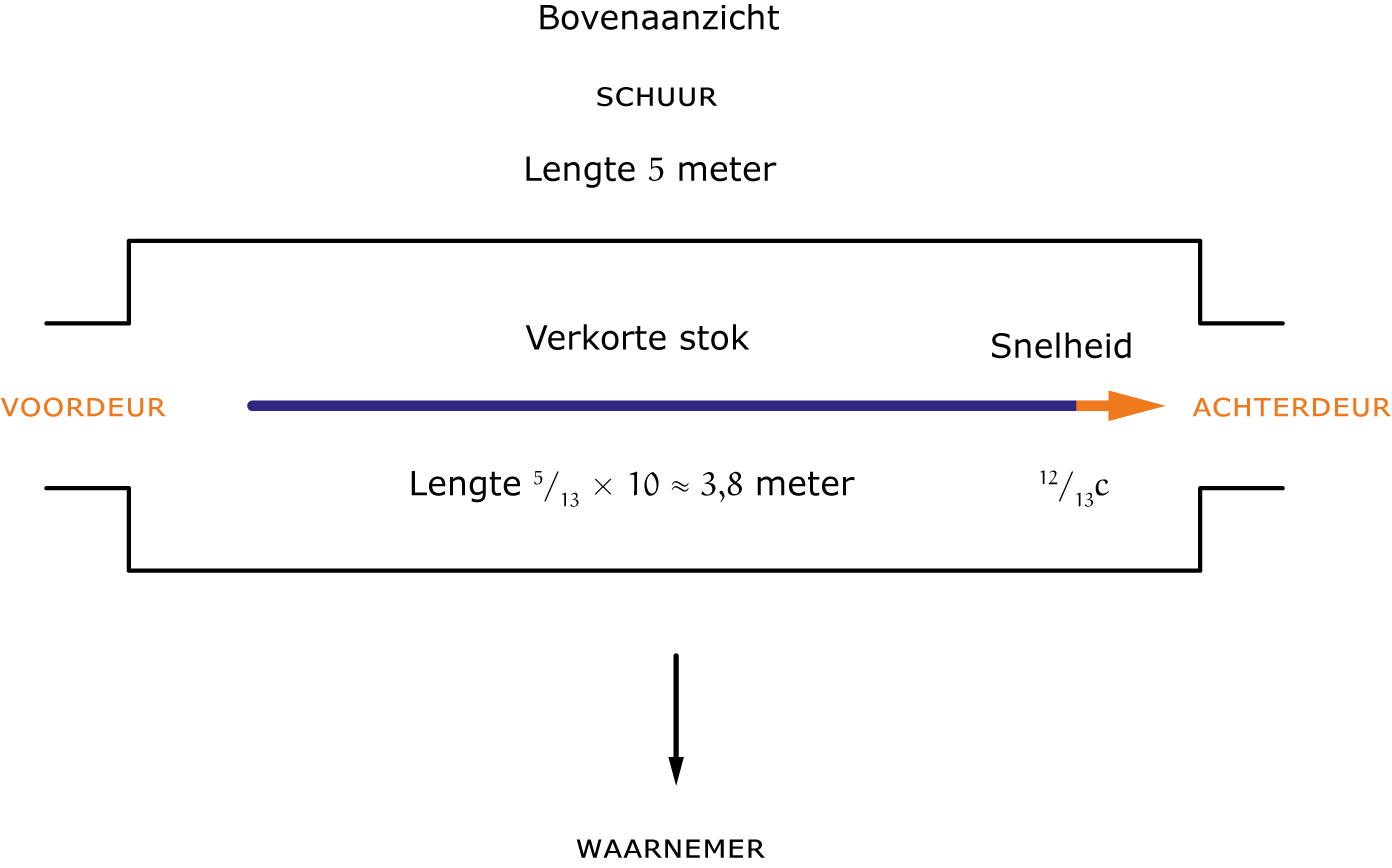
Stel je hebt een houten stok van $L^\prime = 10$ meter lang (gemeten door iemand stil ten opzichte van de stok). Zelf sta je op zekere afstand dwars van een schuur met een lengte van $5$ meter. De stok vliegt op de schuur af, door de openstaande voordeur naar binnen en door de openstaande achterdeur naar buiten. Zie figuur 1. In het gewone leven zul je, als de stok halverwege is, $2{,}5$ meter stok al bij de achterdeur naar buiten zien steken, terwijl je ook $2{,}5$ meter
stok ziet die nog niet door de voordeur heen is. Maar we moeten de zaak natuurlijk relativistisch bekijken. Laten we daarom eens aannemen dat de stok echt snel op de schuur af vliegt: met een snelheid van $\frac{12}{13}c$. We weten inmiddels dat er sprake is van lengtecontractie. De lengte $L$ in het coördinatenstelsel $S$ van de waarnemer bij de schuur is:
$$L=L^\prime\sqrt{1-\frac{v^2}{c^2}}=L^\prime\sqrt{1-\frac{\left(\frac{12}{13}c\right)^2}{c^2}}=\frac{5}{13}\times10 < 5 \mbox{meter}.$$
Het verbazingwekkende is dus dat je de stok in jouw coördinatenstelsel een korte tijd niet ziet, omdat de stok geheel tussen de deuren van de schuur vliegt.
Het zou zelfs mogelijk zijn om de twee deuren heel snel te sluiten. Maar dan zal de stevige stok, die natuurlijk door zijn geweldige snelheid een grote hoeveelheid bewegingsenergie bevat, de vermolmde achterdeur met gemak versplinteren en verkort doorvliegen. Maar als de deuren en de schuur zelf van gigantisch sterk materiaal gemaakt zijn en de schuur zeer goed verankerd is, zal de vliegende stok al versplinterend na een paar keer heen weer gegaan te zijn tussen de gesloten deuren uiteindelijk in stukken tot stilstand komen in de schuur. De bewegingsenergie van de stok zal dan vrijkomen
in de vorm van warmte en een vuurzee zal waarschijnlijk het gevolg zijn.
Hoe lijk Je eEn voOrbIJrazende kUBus te zien?
Relativistische benadering
Beschouw eens een kubus met afmetingen $a^\prime\times a^\prime\times a^\prime$ in zijn eigen coördinatenstel. Stel dat die boven je langs voorbijraast met een snelheid $v$. Het eerste wat je zult zeggen is dat je de kubus vanwege de lengtecontractie verkort ziet tot:
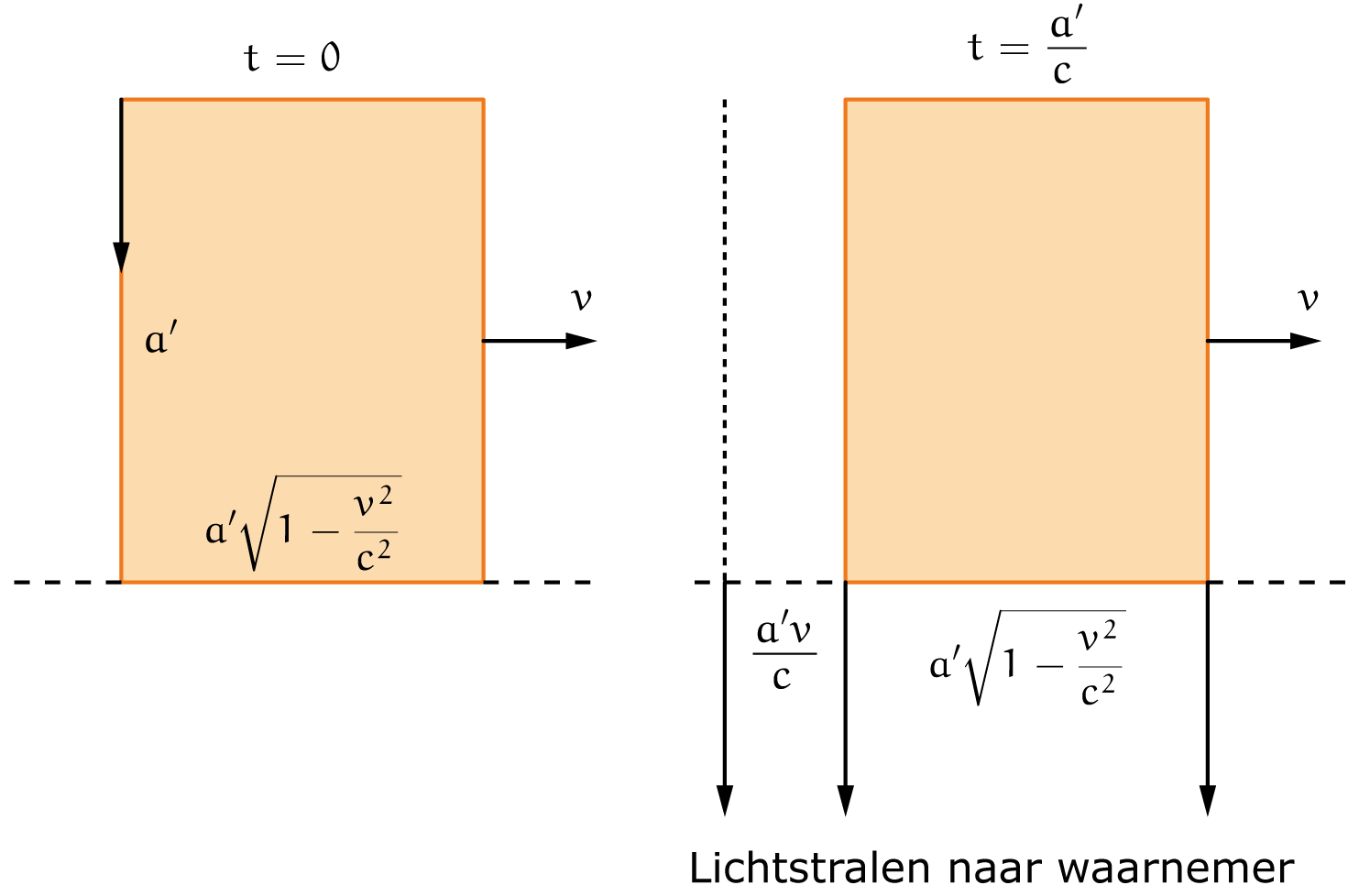
$$a=a^\prime\sqrt{1-\frac{v^2}{c^2}}.$$
Zie figuur 2 met de verkorte kubus op twee tijdstippen. Maar je moet beseffen dat 'een voorwerp zien' betekent dat de lichtstralen afkomstig van dat voorwerp je ogen tegelijkertijd bereiken. Dat geldt voor de lichtstralen vertrekkend van de punten aan de onderkant van de kubus richting je oog er dwars onder. Die lengtecontractie zie je dus echt. Maar beschouw nu eens ook een lichtstraal die vertrekt van de linker bovenhoek van de kubus naar beneden richting je oog. Die lichtstraal schuurt niet langs de zijkant van de kubus, want de kubus beweegt naar rechts. De lichtstraal bereikt de stippellijn getrokken door de onderkant van de kubus na een tijdje $t$:
$$t=\frac{a^\prime}{c}.$$
Op dat tijdstip is de kubus een stukje naar $b$ naar rechts gevlogen:
$$b=vt=a^\prime\frac{v}{c}.$$
Bekijk nu, samen met deze lichtstraal, de twee lichtstralen die op tijdstip $t$ vertrekken van het linker en rechter hoekpunt van de onderkant van de kubus. Deze drie stralen bereiken tegelijkertijd je oog. Je ziet dus de verkorte onderkant, maar ook de linkerzijkant (de tussenliggende stralen doen
natuurlijk ook mee).
Het bijzondere is nu dat voor deze twee lengtes geldt:
$$a^2+b^2=\left(a^\prime\sqrt{1-\frac{v^2}{c^2}}\right)^2+\left(a^\prime\frac{v}{c}\right)^2=a^{\prime 2}.$$
Niet-relativistische benadering
In de niet-relativistische benadering hebben we $v \ll c$, of $v \approx 0$ of $c \rightarrow \infty$. Alle lichtstralen die tegelijkertijd van de kubus vertrekken, bereiken ons oog ook vrijwel tegelijkertijd. Als we dus niet-relativistisch denken en de kubus vliegt precies boven ons langs, zien we alleen een stukje van de zijkant van de kubus als de kubus een stukje gedraaid is. Zie figuur 3.
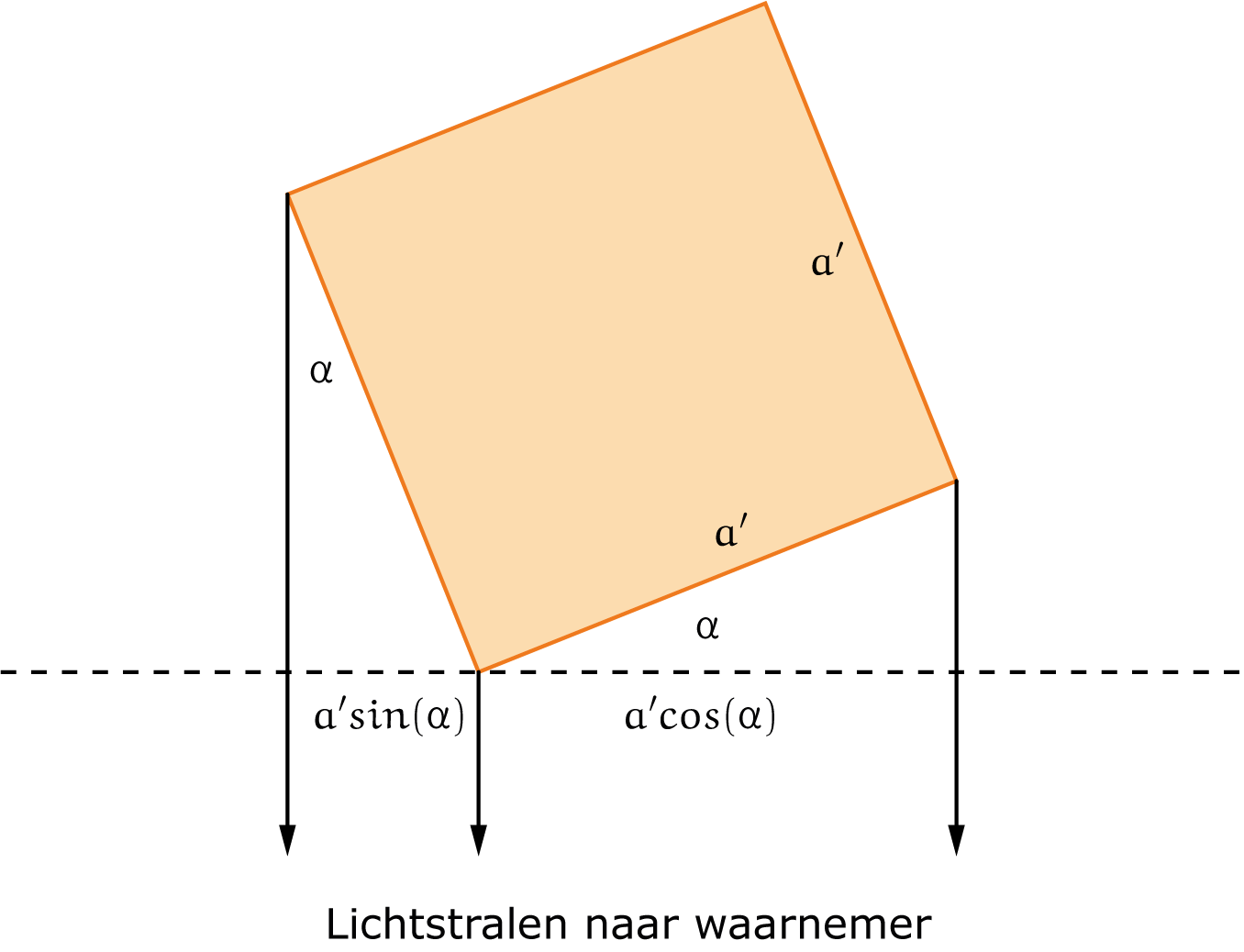
Bij een rotatie over een hoek $\alpha$ zien we de zijkant met een 'breedte' $a^\prime\sin(\alpha)$ en de onderkant 'verkort' tot $a^\prime\cos(\alpha)$. Ook hiervoor geldt:
$$\left(a^\prime\cos(\alpha)\right)^2+\left(a^\prime\sin(\alpha)\right)^2=a^{\prime2}.$$
Het lijkt dus dat we de met relativistische snelheid passerende kubus zien passeren als een niet-relativistische kubus die passeert maar gedraaid is over een hoek $\alpha$ met:
$$\tan(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}=\frac{a^\prime\frac{v}{c}}{a^\prime\sqrt{1-\frac{v^2}{c^2}}}=\frac{\frac{v}{c}}{\sqrt{1-\frac{v^2}{c^2}}}.$$
Bij snelheden $v \ll c$ is de draaiingshoek maar klein ($\tan(\alpha) \approx v/c$). Echter, als $v$ heel dicht bij de snelheid van het licht komt, zie je een steeds breder stuk van de zijkant ($a^\prime v/c \rightarrow a^\prime$) en een steeds meer verkorte onderkant. De schijnbare draaiingshoek wordt dan bijna $90^{\rm o}$ ($\tan(\alpha) \rightarrow \infty$).
Tot slot: een aantal visualisaties van met zeer grote snelheden bewegende voorwerpen (onder andere de kubus) is te vinden op de site www.spacetimetravel.org
Relativiteitstheorie |
