Het doel van het beloftenprogramma is om de veelbelovende talenten een kans te geven zich te verbeteren in wiskunde. Dit gebeurt door middel van theorie en wekelijkse opdrachten, verdeeld in vier thema’s: getaltheorie, meetkunde, algebra en kleine gevallen. De belangrijkste onderdelen van een thema komen naar voren in de theorie met zes bijpassende opdrachten.

Het beloftenprogramma kan een erg grote impact hebben op de leerlingen. Zo zat één van de huidige beloftenprogramma-trainers drie jaar geleden zelf in het beloftenprogramma, en afgelopen zomer heeft hij een IMO-medaille gewonnen.

Kleine gevallen

Bij opdrachten van het thema Kleine gevallen is één ding altijd hetzelfde: je moet iets oplossen voor een algemeen getal (bijvoorbeeld algemene $n$), of voor een erg groot getal (vaak $100$ of $2021$), maar als je dat direct probeert te bewijzen is dat heel erg lastig. Hoe je dit soort opdrachten moet beginnen, is door concrete kleine gevalletjes te proberen (bijvoorbeeld $n = 1, n = 2 \ldots$). Nadat je genoeg van die kleine gevalletjes hebt gedaan, kun je proberen er een patroon in te vinden. En als je dan dat patroon hebt gevonden, wordt het algemene geval oplossen al veel makkelijker. Laten we een opdracht bekijken op hoog beloftenprogrammaniveau uit dit thema.

De opdracht We hebben een $n$ bij $n$ schaakbord met witte en zwarte vakjes $(n \ge 1)$. In elke stap kies je een rechthoek in het bord, en daarin maak je elk wit vakje zwart, en elk zwart vakje wit. Bepaal voor elke $n$ hoeveel stappen je minimaal nodig hebt om te zorgen dat alle vakjes dezelfde kleur hebben.  Voorbeeld van een stap bij $n = 4$:

Dit is een behoorlijk pittige opgave, maar doe gerust een poging als het je leuk lijkt. Verkennen We gaan deze opgave beginnen door een aantal kleine getallen in te vullen voor $n$. Dit zijn onze kleine gevalletjes. Daarna kunnen we proberen hier een patroon in te vinden, om uiteindelijk een bewijs te maken.

$n = 1$

Dit is al allemaal dezelfde kleur, dus zijn er $0$ stappen nodig.

$n=2$

Na een beetje gepruts kom je erachter dat het minimale aantal stappen gelijk is aan twee. En dit kan op twee verschillende manieren. Door de eerste manier kom je misschien op het idee om alle zwarte vakjes met $1$ bij $1$ vierkantjes weg te halen, dit kost dan $n^2$ of $\tfrac12(n^2 - 1)$ stappen. De logica achter de tweede manier is nog niet echt duidelijk hier.

$n = 3$

Ook $n = 3$ kunnen we alles dezelfde kleur maken met twee stappen. Dit kan alleen op deze manier. Deze manier lijkt het meest op de tweede manier van $n = 2$ en het kost minder stappen dan de vier stappen die nodig zouden zijn met alleen maar $1$ bij $1$ vierkantjes. Dit betekent dat we over die laatste aanpak nu niet echt meer na hoeven te denken; die zal hierna nooit meer efficiënter zijn.

$n = 4$

Bij $n = 4$ kom je uiteindelijk op deze oplossing met $4$ stappen. Er zijn meerdere oplossingen met $4$ stappen, maar deze is het simpelst. Je kan hierop uitkomen door te
kijken naar de oplossingen van $n = 2$ en $n = 3$ die op elkaar lijken, daar gebruiken we $1$ bij $n$ en $n$ bij $1$ rechthoeken, en dat doen we hier ook. Maar dit is wel lastig om te zien. Je kan ook op deze oplossing komen door simpelweg heel veel te proberen. Dit is wel een lastige oplossing om te vinden, want in de eerste twee stappen veranderen het aantal witte en zwarte vakjes niet, pas in de laatste twee stappen maken we alle zwarte vakjes wit.

We hebben nu voor een aantal $n$ het aantal stappen gevonden, dan is het vaak handig om dit in een overzichtelijke tabel te zetten:

$\color{White}n$	$1$	$2$	$3$	$4$
$\color{White}{aantal\ stappen}$	$0$	$2$	$2$	$4$

Dit is nog niet echt genoeg om een goed vermoeden uit te kunnen halen. Als je nog geen goed vermoeden hebt is het altijd handig om nog een paar kleine gevallen te doen. Nu kunnen we bijvoorbeeld $n = 5$, $n = 6$ en $n = 7$ gaan bekijken. Het is nu sowieso handig om ons vorige idee van $1$ bij $n$ en $n$ bij $1$ rechthoeken weer te proberen, en als je hier een beetje mee prutst lijkt dat weer de optimale oplossing te geven. Als je het leuk vindt kan je dit zelf proberen. Als je de nieuwe waardes gevonden hebt, kan je de tabel zo uitbreiden:

$\color{White}n$	$1$	$2$	$3$	$4$	$5$	$6$	$7$
$\color{White}{aantal\ stappen}$	$0$	$2$	$2$	$4$	$4$	$6$	$6$

Dit geeft al een veel beter idee van hoeveel stappen er nodig zijn. Je kan nu op het vermoeden komen dat voor even $n$ het aantal stappen gelijk is aan $n$, en voor oneven $n$ gelijk is aan $n - 1$. Dit kan je ook schrijven als $2\left\lfloor\frac{n}{2}\right\rfloor$. De haken staan voor de bewerking entier, wat betekent dat je de uitkomst naar beneden afrondt. Nu we een goed vermoeden hebben kunnen we kijken of we dit kunnen bewijzen.

Bewijs

We willen bewijzen dat het minimale aantal stappen wat nodig is gelijk is aan $2\left\lfloor\frac{n}{2}\right\rfloor$. Dit doen we in 2 delen. We bewijzen dat we het bord één kleur kunnen maken in precies $2\left\lfloor\frac{n}{2}\right\rfloor$ stappen, en we bewijzen dat het niet in minder stappen kan. Laten we beginnen met bewijzen dat het in $2\left\lfloor\frac{n}{2}\right\rfloor$ stappen kan.

We nummeren de rijen en kolommen van het schaakbord, van links naar rechts en van boven naar beneden van $1$ tot $n$:

Zoals we bij het voorbeeld van $n = 4$ al duidelijk zagen, kunnen we met een $n$ bij $1$ rechthoek of een $1$ bij $n$ rechthoek alle vakjes in een hele kolom of rij van kleur wisselen in één stap. Nu kunnen we dit eerst doen bij alle $\left\lfloor\frac{n}{2}\right\rfloor$ even kolommen, dan krijg je een horizontaal patroon zoals na twee stappen bij $n = 4$. Nu kunnen we duidelijk zien dat we bij alle $\left\lfloor\frac{n}{2}\right\rfloor$ even rijen ook de kleuren kunnen wisselen om alles wit te maken. Dus na de $2\left\lfloor\frac{n}{2}\right\rfloor$ stappen is het hele bord wit.

We hebben bewezen dat we in $2\left\lfloor\frac{n}{2}\right\rfloor$ stappen het hele bord dezelfde kleur kunnen maken. Nu moeten we nog bewijzen dat het niet in minder dan $2\left\lfloor\frac{n}{2}\right\rfloor$stappen kan.

Dit is voor veel mensen het moeilijkste deel van deze opgave. Wat vaak helpt is om terug te kijken naar de optimale gevallen van de kleine gevalletjes, en te kijken wat die speciaal maken. Wat opvalt als we terug kijken is dat alle vier hoekpunten van alle rechthoeken in de stappen op de zijkanten van het bord liggen. Door deze observatie ging ik nadenken wat er zo speciaal is aan de zijkanten van het bord, en daardoor kwam ik uiteindelijk op de volgende oplossing.

We kijken specifiek naar paren van twee vakjes die naast elkaar aan de zijkant van het bord liggen. Voor elk van deze paren vakjes kleuren we voor het overzicht de gemeenschappelijke zijde blauw. Dit ziet er zo uit voor $n = 3$ en $n = 4$.

We kunnen hier meteen twee observaties uit halen. Ten eerste zijn er $4(n - 1)$ van dit soort paren. Ten tweede geldt voor elk van deze paren dat de twee vakjes in de beginsituatie verschillend gekleurd zijn. 

In de eindsituatie zijn alle vakjes dezelfde kleur, dus dan geldt ook dat elk vakje van deze paren dezelfde kleur heeft. 

Nu geldt het volgende: twee vakjes van één paar kunnen alleen dezelfde kleur krijgen als er een stap wordt gedaan met een rechthoek waarvan de zijde een blauw lijnstuk overlapt. Dit ziet er zo uit:

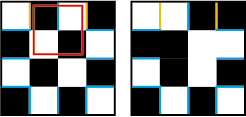
We zien dat voor alle blauwe zijdes na deze stap nog steeds de twee vakjes van het paar verschillend zijn, behalve voor de twee (hier oranje gekleurd) waar de zijde van de rechthoek overheen liep.

Aangezien een rechthoek kan overlappen met maximaal vier van de blauwe lijnstukken, weten we nu dat er minimaal $4(n - 1)/4 = n - 1$ stappen nodig zijn om alle vakjes dezelfde kleur te maken. Dit is precies wat we wilden bewijzen voor
oneven $n$. Maar voor even $n$ willen we bewijzen dat we minimaal $n$ stappen nodig hebben. Hiervoor gebruiken we een bewijs uit het ongerijmde. Dit betekent dat we aannemen dat we voor een even $n$ wel in $n - 1$ stappen alle vakjes dezelfde kleur kunnen maken. Vervolgens proberen we een tegenspraak te vinden. 

We hebben totaal $n - 1$ stappen nodig, dus voor elke stap vallen vier blauwe lijnstukjes samen met de zijden van de rechthoek. Dit halen we uit het feit dat er $4(n - 1)$ blauwe zijdes zijn. Merk op dat we dan niet een van de vakjes in de hoeken van het bord kunnen veranderen van kleur. Want als we een vakje in een hoek van kleur veranderen, dan lag de rechthoek in de hoek van het bord, en dat kan niet want daar is geen blauw lijnstuk. Maar dat betekent dat na $n - 1$ stappen alle hoeken dezelfde kleur hebben als aan het begin. In de beginsituatie hebben de linkerbovenhoek en rechterbovenhoek verschillende kleuren (want $n$ is even), dus aan het einde ook! Dit kan duidelijk niet, want in de eindsituatie
moeten alle vakjes dezelfde kleur hebben. Dit is een tegenspraak!

Het bewijs uit het ongerijmde is nu compleet. Dit betekent dat onze aanname dat we in $n - 1$ stappen alle vakjes dezelfde kleur kunnen maken niet klopt, dus zijn er minimaal $n$ stappen nodig voor even $n$, en dat is precies wat we wilden bewijzen! 

We hebben nu dus bewezen dat het minimale aantal stappen wat nodig is gelijk is aan $n$ voor even $n$, en $n - 1$ voor oneven $n$.