In dit artikel veronderstel ik dat de lezer bekend is met:

• de formules voor $\sin(\alpha \pm \beta)$ en $\cos(\alpha \pm \beta)$
•  sinusfuncties van de vorm $A \cdot \sin(bx + c)$ waarin $A$ de amplitute bepaalt van de grafiek en een cyclus zich uitstrekt over het interval $0 \le bx + c \le 2\pi$. Een cyclus begint dus als $x = -\frac{c}{b}$ en eindigt als $x =\frac{2\pi-c}{b}$. Dit geeft een faseverschuiving van $-\frac{c}{b}$ en een periode van $\frac{2\pi}{b}$. (In dit artikel kijk ik alleen naar gevallen met periode $2\pi$, dus $b = 1$. De keuze voor een andere waarde van $b$ levert dezelfde conclusie.)
• een grafische rekenmachine.

Ik begin met de functie $f(x) = \sin(x) + \cos(x)$. Je verwacht dat $\sin(x)$ en $\cos(x)$ met elkaar gaan 'vechten' en dat de grafiek van hun som iets ingewikkelds of zelfs lelijk is. In plaats daarvan ontstaat er een mooie sinusfunctie met weer periode $2\pi$. Hoe kan dat? Denk aan de formule voor $\sin(x + \alpha)$ met $\alpha =\frac{\pi}{4}$.

Opgave 1 Maak deze redenering af en vind de ander vorm voor $f(x)$.

De functie $f(x)$ is dus een sinusfunctie met periode $2\pi$ maar dit was een zeer speciaal geval met een bijzondere hoek $\alpha$ waar $\sin(\alpha) = \cos(\alpha)$. Hoe zou het gaan met de meer algemene functie $g(x) = A \cdot \sin(x) + B \cdot \cos(x)$ waar $A$ en $B$ constanten zijn? Als je wat keuzes voor de constanten maakt kun je met je grafische rekenmachine zien dat de grafiek van $g(x)$ nog steeds een sinusfunctie is met periode $2\pi$.

 

Opgave 2 Vind een andere vorm voor $g(x)$ zoals in opgave 1. Hint: kijk naar de figuur hiernaast.

Maar $f(x)$ heeft ook een andere vorm als $\cos(x)$ geschreven wordt in de vorm $\sin(x + \beta)$.

Opgave 3 Vind een waarde voor $\beta$. (Neem de waarde het dichtst bij $0$.)

Dus $f(x)$ is een speciaal geval van $h(x) = \sin(x) + \sin(x + \vartheta)$. Met een grafische rekenmachine en een paar waarden van $\vartheta$ kun je zien wat er nu gebeurt: weer een sinusgrafiek met een periode van $2\pi$. Dit vraagt om een verklaring. De twee hoeken van $h(x)$ zijn niet hetzelfde. In het speciale geval van $f(x)$ was $\alpha=\tfrac{1}{2}\beta$. Misschien is er iets te doen met $\tfrac{1}{2}\vartheta$. De functie $h(x)$ is ook te schrijven als

$$h(x)=\sin(x+\tfrac{1}{2}\vartheta-\tfrac{1}{2}\vartheta)+\sin(x+\tfrac{1}{2}\vartheta+\tfrac{1}{2}\vartheta).$$

Opgave 4 Denk nu aan de formule van opgave 1 en gebruik hem twee keer met de hoeken $x+\tfrac{1}{2}\vartheta$ en $\pm\tfrac{1}{2}\vartheta$. Wat is de andere vorm voor $h(x)$?

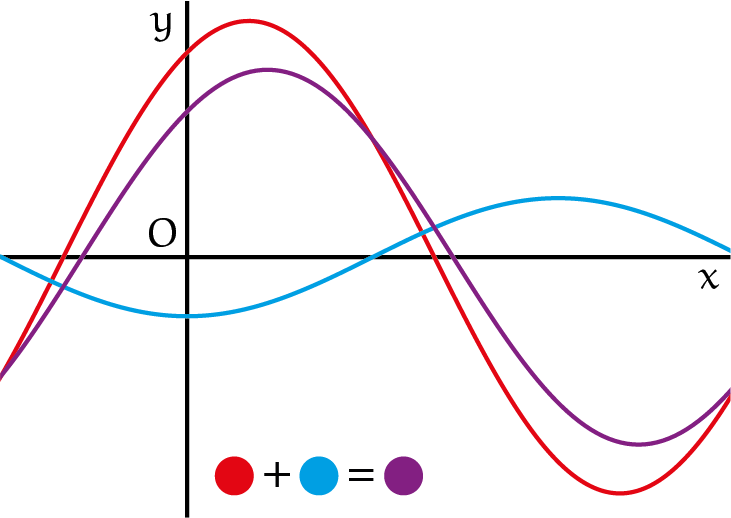
Maar zou zelfs een functie zoals $j(x)=A \cdot \sin(x) + B \cdot sin(x + \vartheta)$ ook een sinusfunctie zijn met periode $2\pi$? Probeer een paar voorbeelden met je grafische rekenmachine. Hier komen alle complicaties tot nu toe samen. Misschien zijn de twee constanten $A$ en $B$ ook te herschrijven zoals hoek $\vartheta$. Dan is $A \cdot \sin(x)$ te herschrijven als:

$$A\cdot \sin(x)=\frac{A+B}{2}\cdot\sin\left(x+\tfrac{1}{2}\vartheta-\tfrac{1}{2}\vartheta\right)+\frac{A-B}{2}\cdot\sin\left(x+\tfrac{1}{2}\vartheta-\tfrac{1}{2}\vartheta\right)$$

en $B\cdot\sin(x+\vartheta)$ kan ook zo'n vorm krijgen. Het eindresultaat in figuur 1 beloont de complicaties onderweg.

Opgave 5 Laat zien dat $j(x)$ ook een sinusfunctie is met periode $2\pi$.

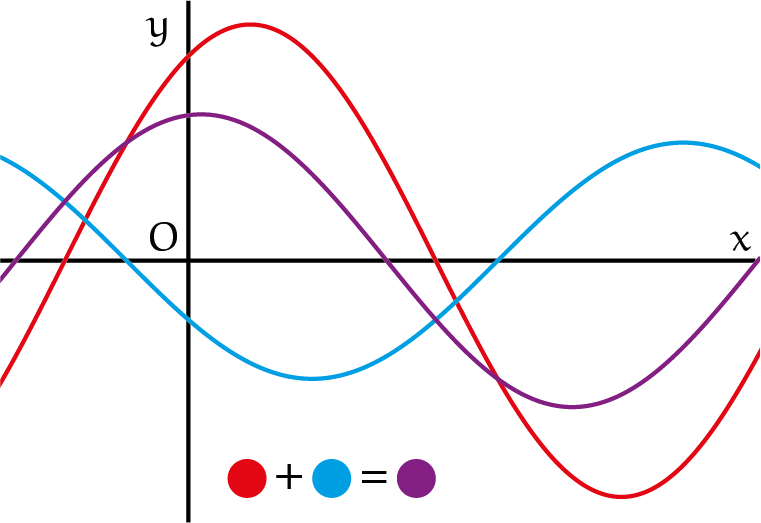
In dit laatste voorbeeld (zie figuur 2) is te zien dat de som van twee sinusfuncties met periode $2\pi$ weer een sinusfunctie is met periode $2\pi$. Dit is het geval, ondanks dat de twee sinusfuncties verschillende amplituden en fasen hebben.

Als laatste verklaar ik de titel van dit stuk. Het woord symfonisch betekent mooi samenklinkend. Ik speel in een amateurorkest. Voor een repetitie of concert gaan wij stemmen. Op een oscilloscoop zijn tonen voor te stellen als sinuskrommen met perioden die corresponderen met de hoogte van de toon, amplituden die corresponderen met de kracht van de toon en faseverschuivingen die corresponderen met de tijd van inzet. Wij zoeken op onze instrumenten dezelfde toon (oftewel dezelfde waarde van b uit de formule) en beginnen te stemmen op verschillende momenten en met verschillende kracht. En als wij klaar zijn klinkt het toch samen als één toon. Nu heb ik een beter idee waarom.

Bekijk oplossing