Opgave 1

$\alpha=\frac{\pi}{4} \rightarrow \cos(\alpha)=\sin(\alpha) = \tfrac{1}{2}\sqrt{2} \rightarrow f(x)=\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)$.

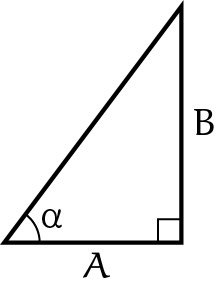
Opgave 2

In figuur 1 zijn $\cos(\alpha)=\frac{A}{\sqrt{A^2+B^2}}$ en $\sin(\alpha)=\frac{B}{\sqrt{A^2+B^2}}$ en dus $g(x)=\sqrt{A^2+B^2}\cdot\sin(x+\alpha)$ waar $\alpha$ een hoek is met deze cosinus en sinus-waarden.

Opgave 3

$\sin(x+\beta)=\sin(x)\cos(\beta)+\cos(x)\sin(\beta)$ en als $\cos(\beta)=0$ en $\sin(\beta)=1$ dan is $\sin(x+\beta)=\cos(\beta)$. Kies $\beta = \frac{\pi}{2}$.

Opgave 4

$\begin{align*}
h(x)&=\sin\left(x+\tfrac{1}{2}\vartheta-\tfrac{1}{2}\vartheta\right)+\sin\left(x+\tfrac{1}{2}\vartheta+\tfrac{1}{2}\vartheta\right)\\
&=\sin\left(x+\tfrac{1}{2}\vartheta\right)\cos\left(\tfrac{1}{2}\vartheta\right)-\cos\left(x+\tfrac{1}{2}\vartheta\right)\sin\left(\tfrac{1}{2}\vartheta\right)\\
&+\sin\left(x+\tfrac{1}{2}\vartheta\right)\cos\left(\tfrac{1}{2}\vartheta\right)+\cos\left(x+\tfrac{1}{2}\vartheta\right)\sin\left(\tfrac{1}{2}\vartheta\right)\\
&=2\cos\left(\tfrac{1}{2}\vartheta\right)\sin\left(x+\tfrac{1}{2}\vartheta\right)
\end{align*}$

Opgave 5

\begin{align*}
j(x)&=\frac{A+B}{2}\sin(x)+\frac{A-B}{2}\sin(x)+\frac{A+B}{2}\sin(x+\vartheta)-\frac{A-B}{2}\sin(x+\vartheta)\\
&=\frac{A+B}{2}\sin\left(x+\tfrac{1}{2}\vartheta-\tfrac{1}{2}\vartheta\right)+\frac{A-B}{2}\sin\left(x+\tfrac{1}{2}\vartheta-\tfrac{1}{2}\vartheta\right)\\
&+\frac{A+B}{2}\sin\left(x+\tfrac{1}{2}\vartheta+\tfrac{1}{2}\vartheta\right)-\frac{A-B}{2}\sin\left(x+\tfrac{1}{2}\vartheta+\tfrac{1}{2}\vartheta\right)\\
&=\frac{A+B}{2}\sin\left(x+\tfrac{1}{2}\vartheta\right)\cos\left(\tfrac{1}{2}\vartheta\right)-\frac{A+B}{2}\cos\left(x+\tfrac{1}{2}\vartheta\right)\sin\left(\tfrac{1}{2}\vartheta\right)\\
&+\frac{A-B}{2}\sin\left(x+\tfrac{1}{2}\vartheta\right)\cos\left(\tfrac{1}{2}\vartheta\right)-\frac{A-B}{2}\cos\left(x+\tfrac{1}{2}\vartheta\right)\sin\left(\tfrac{1}{2}\vartheta\right)\\
&+\frac{A+B}{2}\sin\left(x+\tfrac{1}{2}\vartheta\right)\cos\left(\tfrac{1}{2}\vartheta\right)+\frac{A+B}{2}\cos\left(x+\tfrac{1}{2}\vartheta\right)\sin\left(\tfrac{1}{2}\vartheta\right)\\
&-\frac{A-B}{2}\sin\left(x+\tfrac{1}{2}\vartheta\right)\cos\left(\tfrac{1}{2}\vartheta\right)-\frac{A-B}{2}\cos\left(x+\tfrac{1}{2}\vartheta\right)\sin\left(\tfrac{1}{2}\vartheta\right)\\
&=\left(A+B\right)\sin\left(x+\tfrac{1}{2}\vartheta\right)\cos\left(\tfrac{1}{2}\vartheta\right)-\left(A-B\right)\cos\left(x+\tfrac{1}{2}\vartheta\right)\sin\left(\tfrac{1}{2}\vartheta\right)
\end{align*}

En dit heeft de vorm van $g(x)$ en is dus weer een sinusfunctie met periode $2\pi$.