Veel onschuldige wiskundige puzzels blijken diepe wiskundige structuren te bezitten. Zo ook de tandenstokerpuzzel. Begin met een tandenstoker en leg die verticaal voor je neer (dit is zet 1). Vervolgens leg je aan elk uiteinde van deze tandenstoker een nieuwe tandenstoker, horizontaal en met het middelpunt van de nieuwe tandenstoker rakend aan zo’n uiteinde (dit is zet 2). Dan komen zet 3, zet 4, enzovoorts, waarbij je in elke zet zoveel mogelijk tandenstokers moet neerleggen onder de volgende voorwaarden:

• elke nieuwe tandenstoker moet horizontaal of verticaal liggen;
• twee tandenstokers mogen niet over elkaar heen liggen;
• het middelpunt van elke nieuwe tandenstoker moet raken aan een eindpunt van precies één tandenstoker die er al lag

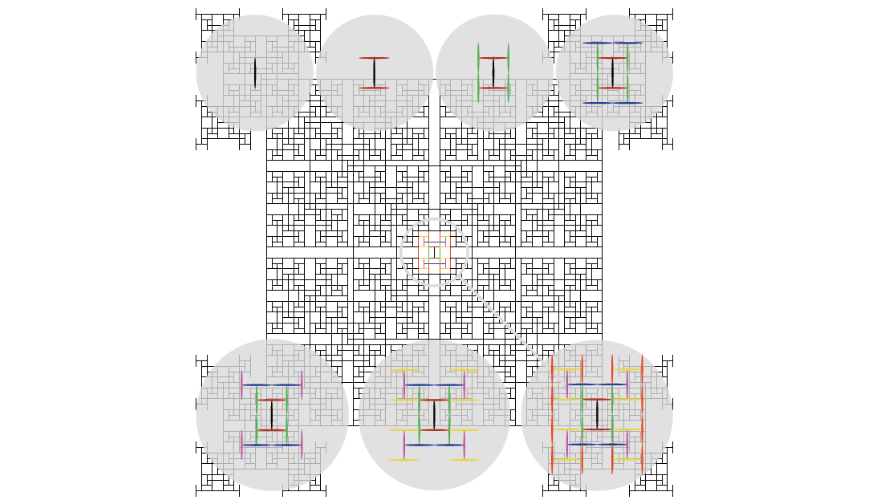
Op de linkerpagina zijn de eerste zeven zetten geïllustreerd; op de achtergrond zie je de situatie na 89 zetten. Het aantal tandenstokers na n zetten kunnen we noteren als $T(n)$. De eerste zeven waarden van $T(n)$ kun je tellen met behulp van de illustratie:

$$1, 3, 7, 11, 15, 23, 35.$$

De rij gaat zo verder: $43, 47, 55, 67, 79, 95, …$ In de Online Encyclopedia of Integer Sequences (OEIS) is de rij te vinden onder nummer A139250. Hij werd in 2008 aan de encyclopedie toegevoegd door de Argentijn Omar Pol. In de OEIS vind je onder andere links naar prachtige animaties die de eerste zoveel zetten in beeld brengen.

Formules

Samen met OEIS-vader Neil Sloane en David Applegate schreef Omar Pol een artikel over de wiskundige eigenschappen van de tandenstokerrij. Wie dat artikel leest (het is gratis beschikbaar op internet, googel maar: “The Toothpick Sequence and Other Sequences from Cellular Automata”), komt er al gauw achter dat de wiskunde achter de tandenstokers niet makkelijk is. Pol en zijn collega’s leiden een formule voor $T(n)$ af. Ze onderscheiden daarbij het geval waarbij $n$ een macht van 2 is, en alle andere gevallen. Als $n = 2^k$, dan geldt

$$T(2^k) = (2^{2k+1} +1)/3. (\star)$$

Na 8 zetten ($k = 3$) bestaat de configuratie dus uit $(2^7 + 1)/3 = 43$ tandenstokers. 

Als $n$ géén macht van 2 is, dan geldt het volgende recursieve verband:

$$T(2^k + i) = T(2^k) + 2T(i) + T(i+1) -1, (\star\star)$$

waarbij $i = 1, …, 2^k -1$. Dus na 12 zetten ($k = 3$ en $i = 4$) is het aantal tandenstokers gelijk aan

$$T(8) + 2T(4) + T(5) – 1 = 43 + 2 \cdot 11 + 15 - 1 = 79.$$

Om ($\star$) en ($\star\star$) te bewijzen, is niet de allerhoogste wiskunde nodig, maar doorzettingsvermogen is wel essentieel. Wie goed voor het bewijs van Pol, Sloane en Applegate gaat zitten, wordt beloond met een fraai staaltje redeneerkunst. Bekijk ook eens de animatie op oeis.org/A139250/a139250.anim.html  en probeer dan vooral $T(n)$ met $n$ een macht van 2 eens uit; dan zie je waarom de machten van 2 een speciale rol spelen in de formule voor $T(n)$.

Je vraagt je misschien af, of er geen eenvoudigere formule dan ($\star\star$) voor $T(n)$ bestaat. Dat is een open probleem in de wiskunde; een andere formule dan ($\star\star$) is tot nog toe niet gevonden!

Verder onderzoek

Op de tandenstokerpuzzel kun je eindeloos variëren. Bijvoorbeeld: wat gebeurt er als de tandenstokers de vorm van bijvoorbeeld een ‘T’, ‘V’ of ‘Y’ hebben (zie oeis.org/A139250/a139250.anim.html)? Of: wat als de tandenstokers niet op een plat vlak worden neergelegd, maar in de (driedimensionale) ruimte (OEIS: A160160)? Op de achterkant van deze Pythagoras zie je een plaatje van de driedimensionale tandenstokerpuzzel (de tandenstokers zijn zwart, de drie rode lijnen vormen een driedimensionaal coördinatenstelsel; de eerste tandenstoker ligt in de zrichting, en dan gaan we verder zoals in het tweedimensionale geval, waarbij we de tandenstokers in zet 2 in de x-richting leggen, in zet 3 in de $y$-richting, in zet 4 in de $z$-richting, in zet 5 opnieuw in de $x$-richting, enzovoort). http://pythagoras.demo.fizz.nl/oeis-a160160

Een heel andere vraag gaat over vierkanten binnen een tandenstokerconfiguratie. Op het omslag van deze Pythagoras zie je de configuratie na 32 zetten. Daarin zijn vierkanten met zijden 1, 2, 3, 4, 6, 7 en 8 groen gekleurd (aangenomen dat de tandenstokers lengte 2 hebben). De configuratie bevat geen vierkant met zijde 5. Lukt het na méér dan 32 zetten om wél een vierkant met zijde 5 te vinden? Uiteraard moet de rand van het vierkant helemaal met tandenstokers bedekt zijn.

Kortom: er valt veel te experimenteren en te ontdekken. Zet je tanden er maar eens in!