In Pythagoras 59-5 stond een artikel van Dave Odegard waarin hij patronen opbouwde uit gelijkzijdige driehoeken, vierkanten en regelmatige zeshoeken. In dit artikel slaan we een andere weg in: we maken alleen gebruik van ruiten. Op het omslag van deze Pythagoras staat een voorbeeld van een tekening die je kunt maken. Er lijkt zelfs perspectief in te zitten.

Enkele voorbeelden

Als je één soort ruit kiest, dan kun je zonder problemen het vlak vullen, maar dat is wel erg saai. We gaan dus direct naar minimaal twee verschillende ruiten. Dat kan met de twee ruiten in figuur 1.

Figuur 1

De hoeken van deze ruiten zijn $36^{\rm o}$ en $144^{\rm o}$ voor de linker ruit en $72^{\rm o}$ en $108^{\rm o}$ voor de rechter ruit. Je kunt je waarschijnlijk niet direct voorstellen dat je met deze twee ruiten iets bijzonders kunt maken.

Figuur 2

Vandaar in figuur 2 een paar tekeningen met deze twee ruiten. Deze twee tekeningen zijn ook nogal saai. Maar je kunt ook andere tekeningen maken, zoals in figuur 3. 

Figuur 3

Hier komt Penrose om de hoek kijken. Met een paar extra restricties op het gebruik van deze twee ruiten kun je bewijzen dat je tekeningen kunt maken die nergens herhalen bij translaties. In Pythagoras 41-3 is hier eerder aandacht aan besteed. (De tekening hierboven voldoet niet aan de regels van Penrose.) De volgende stap die je kunt maken is kijken naar figuren die worden opgebouwd uit drie ruiten. In figuur 4 zijn drie ruiten afgebeeld met hoeken

$\frac{180^{\rm o}}{7}$ en $\frac{1080^{\rm o}}{7}$ (links), $\frac{360^{\rm o}}{7}$ en $\frac{900^{\rm o}}{7}$ (midden) en $\frac{540^{\rm o}}{7}$ en $\frac{720^{\rm o}}{7}$ (rechts).

Figuur 4

Hiermee kun je allerlei tekeningen maken. Het omslag van het vorige nummer (Pythagoras 59-5) was met deze ruiten opgebouwd. Andere voorbeelden zie je in figuur 5. 

Figuur 5a

Figuur 5b

De algemene manier om te werken met ruiten is dat je eerst een hoek kiest: $\frac{180^{\rm o}}{K}$, waarbij $K$ een geheel getal is, $K \ge 2$. De ruiten bevatten hoeken die een veelvoud zijn van $\frac{180^{\rm o}}{K}$. Het aantal ruiten dat je kunt construeren is $K/2$ (als $K$ even is of $(K - 1)/2$ als $K$ oneven is. Voor het omslag van dit nummer is gekozen voor $K = 52$. Met een dergelijke grote waarde van $K$ kun je $26$ ruiten creëren. Al die ruiten kun je een kleur geven. Dat kan door langs de regenboog kleuren toe te kennen, maar het kan ook door schakeringen van donker naar licht te gebruiken (hoe kleiner de hoeken in een ruit, des te donkerder wordt de betreffende ruit). Dat levert prachtige effecten op. In figuur 6 zie je nog een paar tekeningen gebaseerd op Schoenmeetkunde.

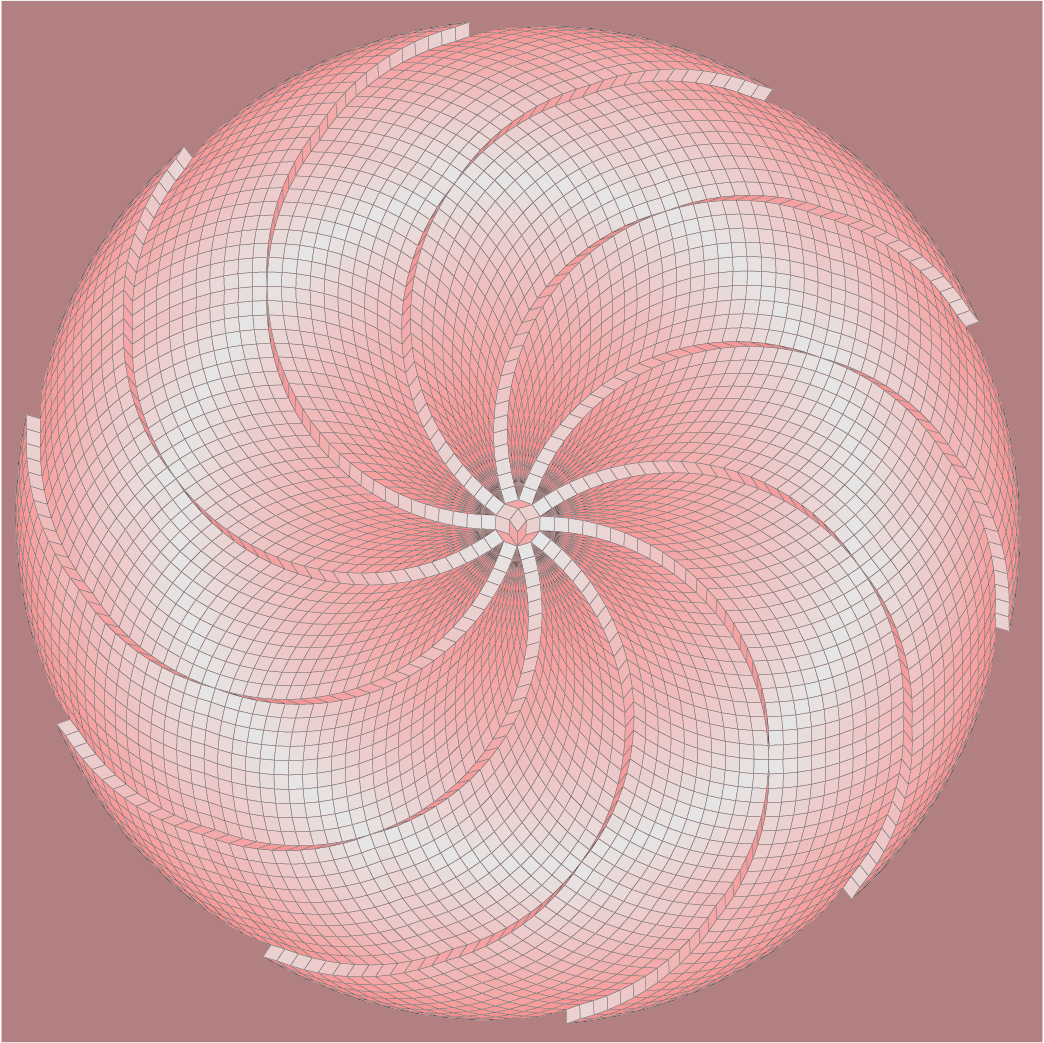
Figuur 6a

Figuur 6b

De linker tekening is gemaakt met $K = 50$, bij de rechter is $K = 51$. Je hoeft er niet voor te kiezen om iets regelmatigs te maken. In figuur 7 een voorbeeld van iets dat niet zo regelmatig is ($K = 53$).

Figuur 7