Bij tennis wordt de bal met een opslag in  het spel gebracht. Beide spelers mogen  om en om een game lang serveren.  Bij elk punt heeft degene die mag serveren  twee kansen. Hij speelt een eerste service,  en als die fout is, een tweede service. Is de  tweede service ook fout, dan gaat het punt  direct naar de tegenstander. Dit noemen we  een dubbele fout. De meeste spelers nemen  wat meer risico op de eerste service door de  bal wat harder te slaan, of meer op de hoek  van het servicevak te richten. Is de eerste  service uit of in het net, dan nemen ze flink  minder risico met de tweede service. Maar  hoeveel risico is optimaal? Geoff en Graham  Pollard hebben een manier bedacht om dit  te berekenen.

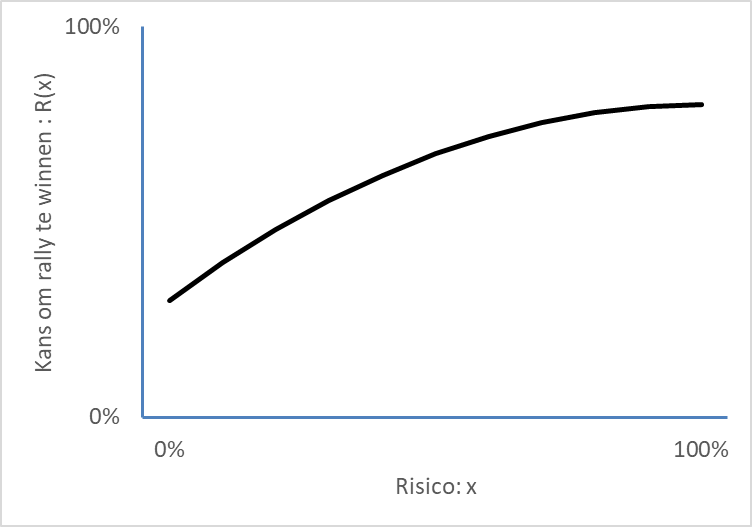
Om te beginnen moet je weten wat het  effect is van meer of minder risico nemen.  Noem de hoeveelheid risico $x$, waarbij $x$  tussen $0$ en $1$ ligt. We definiëren risico zo  dat de kans dat de service goed is $(1 - x) $ is. Een speler kan bijvoorbeeld harder  slaan, of meer op de hoek van het serviceveld  mikken. Noem de kans om de rally te  winnen nadat je een goede service hebt  geslagen waarbij je risico x nam $R(x)$. Het is  duidelijk dat $R(x)$ moet stijgen als $x$ stijgt.  Een voorbeeld van een mogelijk verband is  te zien in figuur 1.

Schematische weergave van het verband tussen de hoeveelheid risico en de kans om de rally te winnen na een goed geslagen service.

Hoe ziet dit verband er precies eruit? Het  meest eenvoudige is om uit te gaan van een  rechte lijn, een lineair verband. Maar Geoff  en Graham Pollard analyseerden veel wedstrijden  op professioneel niveau, en kwamen  erachter dat dat niet kan kloppen. Volgens  hen geldt er een kwadratisch verband:  

$$R(x) = a + b \cdot x + c \cdot  x^2.$$

Ze vonden voor mannelijke toppers een  waarde voor $c$ van $-0{,}6$ en voor vrouwen  een $c$ van $-0{,}3$. Omdat $c$ negatief is levert meer risico nemen steeds iets minder op.

Stel dat $a$, $b$ en $c$ bekend zijn. Hoe kunnen we dan de optimale hoeveelheid risico berekenen? De eerste stap is om te bepalen  hoe de kans om het punt te winnen als je  serveert afhangt van de hoeveelheid risico  op de eerste service $(x_1)$ en de tweede  service $(x_2)$. Er zijn twee manieren om een  punt te winnen. De eerste mogelijkheid is  dat de eerste service in is $(\mbox{kans } 1 - x_1)$, en je daarna de rally wint $(\mbox{kans }R(x_1))$. De  tweede optie is dat de eerste service fout is  $(\mbox{kans }x_1)$, de tweede service goed $(\mbox{kans }1 - x_2)$, en je daarna de rally wint $(\mbox{kans }R(x_2))$. De kans om het punt te winnen is  dus:  $P(x_1, x_2) = (1- x_1) \cdot  R(x_1) +  x_1 \cdot  (1 - x_2) \cdot  R(x_2) $ Vervolgens willen we de optimale hoeveelheid  risico $x^*_1$ en $x^*_2$ vinden. We beginnen met  $x^*_2$ Als de eerste service fout is, heb je nog  één kans om de service goed te slaan. Wat  er daarvóór is gebeurd doet er niet meer  toe, de speler moet een tweede service  slaan die de kans om het punt te winnen  maximaliseert. We hoeven daarom alleen te  kijken naar $(1- x_2) \cdot  R(x_2)$, de kans om het  punt alsnog te winnen na een fout geslagen  eerste service. Als we de haakjes wegwerken  krijgen we het volgende:  

$$(1- x+2) \cdot R(x_2) = a + (b- a) \cdot x_2 +(c -b) \cdot x^2_2 - cx^3_2.$$

Hoe bepaal je voor welke waarde van $x_2$ dit  maximaal is? Door de afgeleide gelijk te  stellen aan $0$:

$$(b -a) +2(c- b)x_2 -3c\cdot x_2^2= 0.$$

Nu houden we een vergelijking over die we  op kunnen lossen met de abc-formule. Na  wat herschrijven krijgen we:

$$x^*_2 = \frac{(c-b)\pm\sqrt{(c-b)^2+3c(b-a)}}{3c}.$$

We moeten de oplossing met het plusteken  gebruiken, omdat we anders een oplossing  boven de $1$ krijgen voor realistische waarden  van $a$, $b$ en $c$. Nu we $x^*_2$ en dus ook $R(x^*_2)$  weten kunnen we die invullen in de formule  voor $P(x_1, x_2)$ en op dezelfde manier ook  de optimale hoeveelheid risico op de eerste  service berekenen. Kun je zelf narekenen dat  daar het volgende uitkomt?

$$x^*_1=\frac{(c-b)+\sqrt{(c-b)^2+3c(b-a+(1-x^*_2)R(x^*_2))}}{3c}.$$

Laten we dit eens toepassen op een echte  wedstrijd, en kijken of we toptennissers  advies kunnen geven. Op 14 juli 2019  speelden Novak Djokovic en Roger Federer  de finale van Wimbledon tegen elkaar. Het  was een enorm lange en spannende wedstrijd.  Na vijf uur spelen won Djokovic met  7-6, 1-6, 7-6, 4-6, 13-12. In tabel 1 zijn de  wedstrijdstatistieken te zien.  

Tabel 1
		Djokovic		Federer
Risico 1e service: $x_1$		$37{,}90\%$		$37{,}40\%$
Risico 2e service: $x_2$		$10{,}80\%$		$7{,}90\%$
Punten gewonnen op de 1e service: $R(x_1)$		$74{,}30\%$		$78{,}70\%$
Punten gewonnen op de 2e service: $R(x_2)$		$52{,}70\%$		$55{,}70\%$
Wedstrijdstatistieken van de finale op Wimbledon tussen Djokovic en Federer

Beide spelers sloegen in ruim $60\%$ van  de gevallen hun eerste service goed. Hun  tweede service was rond de $90\%$ van de  keren goed. Ondanks dat Federer verloren  heeft, zien zijn statistieken er wat beter uit.  Hij wint vaker de rally als zijn service goed  is. In totaal heeft hij ook net wat meer punten  gewonnen dan Djokovic, mede dankzij  de tweede set die hij dik heeft gewonnen.  Laten we nu eens uitgaan van het kwadratische  verband tussen $x$ en $R(x)$ met een  waarde van $c = -0{,}6$. Omdat we voor beide  spelers twee punten op de grafiek kennen,  $(x_1, R(x_1))$ en $(x_2, R(x_2))$, kunnen we ook de  waarde van $a$ en $b$ bepalen. Voor Djokovic  vinden we dan $R(x) = 0{,}42 + 1{,}09 \cdot x - 0{,}6\cdot x^2$ en voor Federer $R(x) = 0{,}48 +  1{,}05 \cdot x - 0{,}6\cdot x^2$. Vullen we deze waardes  in in de formules om de optimale hoeveelheid  risico te bepalen, dan zien we dat beide  spelers beter meer risico hadden kunnen  nemen op zowel de eerste als tweede service!

Tabel 2
		Djokovic		Federer
$x_1$		$37{,}90\%$		$37{,}40\%$
$x^*_1$		$45{,}40\%$		$44{,}00\%$
$x_2$		$10{,}80\%$		$7{,}90\%$
$x^*_2$		$22{,}70\%$		$19{,}40\%$
$P(x_1,x_2)$		$63{,}90\%$		$68{,}50\%$
$P(x^*_1,x^*_2)$		$65{,}20\%$		$69{,}50\%$
Werkelijke en optimale servicestrategie en de kans om het punt te winnen

Als ze de optimale strategie gebruiken,  stijgt de kans om het punt te winnen op  eigen  service met ruim een procent. Dat lijkt  misschien niet veel, maar als je bedenkt dat  Federer twee matchpoints heeft gehad op  eigen service, dan telt elke procent.

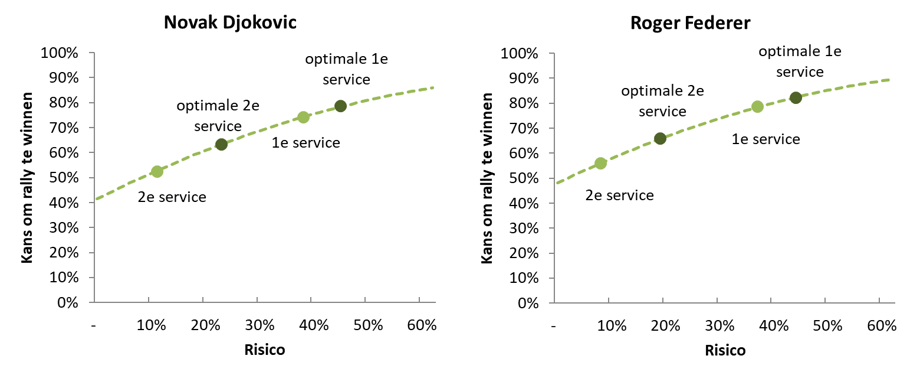
Verband tussen risico en kans om de rally te winnen voor beide spelers op basis van de wedstrijdstatistieken.

Moeten de spelers deze strategie meteen  toe gaan passen? We moeten voorzichtig  zijn met het aanpassen van de eerste  service. De optimale eerste service ligt  buiten de twee punten op de grafiek die uit  de wedstrijd volgen, we hebben geëxtrapoleerd.  Dit punt is ook wat gevoeliger voor  de waarde van $c = -0{,}6$ die we hebben  gekozen dan de optimale tweede service.  Maar als we op deze manier meer wedstrijden  analyseren, ook met andere waardes  voor $c$, komt één conclusie vaak terug:  spelers zouden meer risico moeten nemen  met hun tweede service, en de extra  dubbele fouten voor lief moeten nemen. Er  zijn zelfs wedstrijden waarbij één van de  twee spelers de tweede opslag beter als een  eerste opslag had kunnen slaan. Waarom  doen ze dat dan niet? Waarschijnlijk zijn ze  te bang om het punt gelijk te verliezen met  een dubbele fout, ook al laat wiskunde zien  dat dat onterecht is.    

Bronnen

Pollard, G. N. (2008). What is the  best serving strategy? J Med Sci  Tennis, 13(2), 34-38.  

Wedstrijdstatistieken:  www.flashscore.nl