Bovenaan zie je een gipsmodel en een Surfer-plaatje van het zogeheten Clebsch-oppervlak. Dit oppervlak voldoet aan de vergelijking $648x^2y – 216y^3 – 216x^2z – 216y^2z + 27z + 108z^2 + 113z^3 = 0$. Gipsmodellen van algebraïsche oppervlakken werden vroeger – toen er nog geen geavanceerde softwarepakketten bestonden – veel gemaakt. Op sommige wiskunde-instituten van universiteiten zijn gipsmodellen in vitrines tentoongesteld. Het gipsmodel dat hier is afgebeeld, is van de universiteit van Göttingen. Op het Clebsch-oppervlak liggen 27 rechte lijnen, die je op het gipsmodel kunt herkennen. 

Je weet dat bij de vergelijking $y = x^2$ een parabool hoort. En misschien weet je ook dat bij $x^2 + y^2 = 1$ een cirkel hoort. Hoe zit het als we een dimensie hoger gaan? Bij $x^2 + y^2 + z^2 = 1$ hoort een bol. Maar hoe ziet het oppervlak van $x^2 + y^2 – z^2 = 1$ eruit?

Om dit te zien is er een prachtig programma beschikbaar waarin je zelfs de meest ingewikkelde oppervlakken in drie dimensies zichtbaar kunt maken. Het heet Surfer en is te downloaden van http://imaginary.org/program/surfer. Het programma is eenvoudig te bedienen en wijst grotendeels voor zich. Je typt de vergelijking in het vak rechtsonder en als het goed is verschijnt meteen het bijbehorende oppervlak. Dat oppervlak kun je door slepen met de muis aan alle kanten bekijken. Als de kleuren je niet bevallen, kun je die veranderen.

Vanaf het menu Start kun je diverse oppervlakken bewonderen met hun vergelijkingen in de categorieën ‘Tutorial’, ‘Fantasy Surfaces’ en ‘World Record Surfaces’. Mooie voorbeelden kun je zien in de galerij van Valentina Galata op de Surferpagina. Maar het is natuurlijk nog leuker om zélf je oppervlakken te maken. Het lukraak invoeren van vergelijkingen levert doorgaans geen interessante figuren op. Om dat wel te bereiken, zul je wat gedisciplineerder te werk moeten gaan en gebruik moeten maken van een paar vuistregels die op wiskundige principes gebaseerd zijn.

De vergelijkingen die in dit artikel staan, heb ik in een bestand verzameld, zie http://www.staff.science. uu.nl/~beuke106/SurferModellen.txt. Van daaruit kun je de vergelijkingen makkelijk ‘copy-pasten’. Ook kun je daar meteen zien dat je voor vermenigvuldiging van twee uitdrukkingen een *-teken moet gebruiken. En voor de decimale komma gebruik je een punt, zoals in het Engels gebruikelijk is.

Omwentelingsfiguren We starten met een gewone grafiek, bijvoorbeeld de parabool, met de vergelijking $y = x^2$. Alleen, met het oog op wat komen gaat, noemen we de verticale as de z-as en de horizontale as de $r$-as. De waarde $r$ van een punt is de afstand tot de $z$-as. De parabool heeft nu de vergelijking $z = r^2$. Nu wentelen we de grafiek om de $z$-as, waarbij de $r$-as dus in de rondte draait en een vlak loodrecht op de $z$-as vormt. We geven dit vlak de gewone $x,y$-coördinaten en er geldt $r = √(x^2 + y^2)$. Dus de omwentelingsfiguur heeft de vergelijking $z = r^2 = x^2 + y^2$. Deze figuur, die dus bij $–z + x^2 + y^2 = 0$ hoort, heeft de vorm van een (ouderwetse) fietslamp; in jargon: een paraboloïde (zie figuur 1).

Laten we nu de parabool op zijn kant zetten, dus $r = z^2$. Wentelen van deze figuur rond de $z$-as geeft $√(x^2 + y^2) = z^2$. Helaas slikt Surfer geen uitdrukkingen met een wortelteken, dus moeten we kwadateren: $x^2 + y^2 = z^4$. Het oppervlak dat bij $–z^4 + x^2 + y^2 = 0$ hoort, zie je in figuur 2.

Een kleine variatie: we schuiven de liggende parabool naar links. Dat wordt $r = z^2 – 1$. Als we $r$ weer door $√(x^2 + y^2)$ vervangen en vervolgens kwadrateren, krijgen we $x^2 + y^2 = (z^2 – 1)^2$. Het oppervlak bij $x^2 + y^2 – (z^2 – 1)^2 = 0$ zie je in figuur 3.

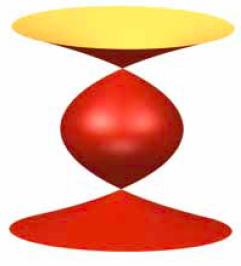
Iets nieuws: neem de cirkel met middelpunt (1, 0) en straal $a$. In het $r,z$-vlak heeft deze de vergelijking $(r – 1)^2 + z^2 = a^2$. Haakjes wegwerken geeft $r^2 – 2r + z^2 + 1 – a^2 = 0$. Voor de omwentelingsfiguur vervangen we $r$ door $√(x^2 + y^2)$. We krijgen $x^2 + y^2 – 2√(x^2 + y^2) + z^2 + 1 – a^2 = 0$. Helaas staat er nu nog steeds een wortelteken. Om dit te verhelpen, brengen we $2√(x^2 + y^2)$ naar rechts en kwadrateren we:

$$(x^2 + y^2 + z^2 + 1 – a^2)^2 = 4(x^2 + y^2).$$

In figuur 4 zie je het plaatje van

$$(x^2 + y^2 + z^2 + 1 – a^2)^2 – 4(x^2 + y^2) = 0, $$

met $a = 0,5$. Varieer zelf de waarde van $a$ en probeer te begrijpen wat er gebeurt.

Opblazen van krommen

Surfer kan geen plaatjes van krommen tekenen. Bijvoorbeeld de cirkel in $x^2 + y^2 – 1 = 0$ geeft een cilinder. Dit komt natuurlijk doordat z niet in de vergelijking voorkomt en daarom een willekeurige waarde kan hebben. In figuur 5 zie je de cilinder samen met het vlak $z = 0$. Hiertoe tik je $z(x^2 + y^2 – 1) = 0$ in (vergeet in Surfer niet het vermenigvuldigingsteken * te gebruiken). Dit geeft alle punten die ofwel op de cilinder liggen ofwel op het vlak $z = 0$.

Eigenlijk zouden we de doorsnijding van deze twee figuren willen zien. Dat is een echte cirkel die voldoet aan de twee vergelijkingen $x^2 + y^2 – 1 = 0$ en $z = 0$. We zouden ze door één vergelijking kunnen vervangen, namelijk $(x^2 + y^2 – 1)^2 + z^2 = 0$. Beide kwadraten moeten immers nul zijn. In Surfer blijkt dat we niet veel zien. Dat komt doordat een cirkel geen oppervlak is. Dit verandert als het rechterlid niet gelijk aan 0 is. In figuur 6 zie je het oppervlak bij

$$(x^2 + y^2 – 1)^2 + z^2 = a^2$$

met $a = 0,1$.

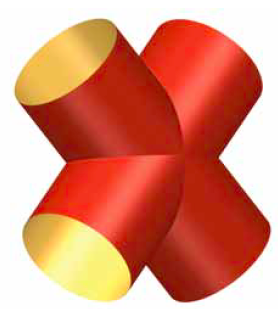
Laten we nu eens kijken naar de doorsnijding van twee cilinders, bijvoorbeeld $x^2 + y^2 – 1 = 0$ en $x^2 + z^2 – 1 = 0$ (zie figuur 7). De vereniging van de twee cilinders wordt door $(x^2 + y^2 – 1)(x^2 + z^2 – 1)= 0$ gegeven. Hoe kunnen we het in Surfer voor elkaar krijgen dat we alléén die doorsnijding in beeld zien? Dit kan door niet het product maar de som van de kwadraten te nemen: $(x^2 + y^2 – 1)^2 + (x^2 + z^2 – 1)^2 = 0$. Alleen zien we dan niets. Daarom zetten we weer $a^2$ in het rechterlid:

$$(x^2 + y^2 – 1)^2 + (x^2 + z^2 – 1)^2 = a^2.$$

In figuur 8 zie je het resultaat voor $a = 0,1$. Als we het oorspronkelijke idee – de doorsnijding van twee cilinders – loslaten, is het leuk om met verschillende waarden van $a$ te experimenteren.

Puntverzamelingen opblazen

Hetzelfde idee kunnen we ook voor punten uitvoeren. Bijvoorbeeld het punt (0, 0, 0) kunnen we geven door het drietal vergelijkingen $x = 0, y = 0$ en $z = 0$. Deze kunnen we vervangen door de enkele vergelijking $x^2 + y^2 + z^2 = 0$. In Surfer zien we echter niets. Kijken we echter naar $x^2 + y^2 + z^2 = a^2$ (met $a > 0$), dan krijgen we een bol – een ‘opgedikte (0, 0, 0)’, zeg maar.

Kijk nu eens naar de punten $(x, y, z)$ die voldoen aan de vergelijkingen $x^2 = 1, y^2 = 1$ en $z^2 = 1$. Natuurlijk zijn dit de punten $(\pm1, \pm1, \pm1)$, de hoekpunten van een kubus. We kunnen deze punten door de ene vergelijking $(x^2 – 1)^2 + (y^2 – 1)^2 +(z^2 – 1)^2 = 0$ geven. Wederom zien we niets in Surfer, maar wel bij de vergelijking

$$(x^2 – 1)^2 + (y^2 – 1)^2 + (z^2 – 1)^2 = a^2.$$

Voor heel kleine $a$ zien we de kubushoekpunten zitten: figuur 9 toont het plaatje als $a = 0,1$. Wat zou er gebeuren als a groter wordt? Als $a = 1$ ziet het oppervlak eruit als in figuur 10. Experimenteer zelf met nog grotere waarden van $a$.

Het idee van het opblazen van punten kunnen we veralgemeniseren. Start bijvoorbeeld met de punten $(x, y, z) $die voldoen aan $x(x^2 – 1) = 0, y(y^2 – 1) = 0$ en $z(z^2 – 1) = 0$. Dit zijn 27 punten.

Bekijk nu de figuur bij

$$x^2(x^2 – 1)^2 + y^2(y^2 – 1)^2 + z^2(z^2 – 1)^2 = a^2$$

als $a$ varieert. Voor $a = 0,1$ en $a = 0,385$ krijg je de figuren 11 respectievelijk 12.

Boetseren

Met de ideeën die we tot nu toe hebben besproken, kunnen we gaan knutselen. Kijk maar eens naar $((x – 2)^2 + y^2 + z^2 – 2)((x + 2)^2 + y^2 + z^2 – 2) = 0.$ Dit geeft twee bollen. En de familie $((x – 2)^2 + y^2 + z^2 – 2)((x + 2)^2 + y^2 + z^2 – 2) – 10a = 0$ geeft voor $a < 0,4$ twee losse figuren. Als $a > 0,4,$ zitten ze vast. In figuur 13 zie je wat je krijgt als $a = 0,4.$

Laten we als variant de standaardbol (met straal 1) $x^2 + y^2 + z^2 – 1 = 0$ nemen en de ‘triviale’ bol (dat is de bol met straal 0) $(x – 1)^2 + y^2 + z^2 = 0$. Bekijk nu de familie

$$a + (x^2 + y^2 + z^2 – 1)((x – 1)^2 + y^2 + z^2) = 0.$$

Voor $a = 0,1$ krijg je figuur 14: je ziet dat we een deuk in de bol hebben gemaakt. En voor $a = –0,1$ krijg je figuur 15: een uitstulping.

Laten we nu een deuk maken in de torus $(x^2 + y^2 + z^2 + 1 – 0,25)^2 – 4(x^2 + y^2) = 0$. We doen dit door de torus te combineren met $(x – 2)^2 + y^2 + z^2 = 0$. Bekijk nu

$$4a + ((x – 2)^2 + y^2 + z^2)((x^2 + y^2 + z^2 + 1 – 0,25)^2 – 4(x^2 + y^2)) = 0$$ 

voor diverse waarden van a. De figuren 16 en 17 laten zien wat je krijgt voor $a = 0,2441$ respectievelijk $a = 1$.

Je kunt nu je fantasie de vrije loop laten, cilinders of vlakken met bollen versmelten, tori combineren, enzovoorts. Een fraai experiment is om de drie cilinders $x^2 + y^2 = 1, x^2 + z^2 = 1$ en $y^2 + z^2 = 1$ te laten samensmelten. Neem

$$–0,05a + (x^2 + y^2 – 1)( x^2 + z^2 – 1)( y^2 + z^2 – 1) = 0$$

en kijk met name wat er binnenin de cilinders gebeurt als $a$ klein is.

Openingstijden, activiteiten en heel veel achtergrondmateriaal van de reizende tentoonstelling Imaginary vind je op http://www.imaginarymaths.nl.