In het leuke boek van Pickover wordt, gekoppeld aan een jaartal, een aansprekend idee of een nieuwe ontwikkeling uit de wiskunde kort beschreven. In het jaar 1969 is gekozen voor die onverlichtbare kamer van Tokarsky. Het is een ruimte met allemaal rechte, verticale (binnen) spiegels, waarbij de rand zichzelf niet doorsnijdt en geen 'gaten' bevat. 'Kan er een ruimte bestaan, die niet vanuit elk punt geheel kan worden verlicht', was in 1969 de vraag en zo ja, wat is dan het minimale aantal rechte wanden?

George Tokarsky vond in 1995 de oplossing met 26 wanden in figuur 1. In 1997 vond David Castro een oplossing met 24 wanden. In de kamer van Castro (figuur 2) zijn de twee bedoelde punten aangegeven; ze liggen in het verlengde van de lange horizontale wand. Hier blijkt tevens de afspraak dat twee punten niet kunnen worden verbonden door een lichtstraal als die (delen van) de rand raakt. Deze afspraak zullen we ook hanteren bij de variant die straks volgt.

Je zou kunnen zeggen dat het 'spiegelgetal' van deze twee vormen 'oneindig' is. Met het spiegelgetal van een vorm bedoel ik het aantal spiegelingen (of spiegelpunten) dat in het meest ongunstige geval nodig is om vanuit het ene punt van die vorm naar het andere te komen met een (oneindig gedachte) lichtstraal. Een gewoon vierkant heeft dan spiegelgetal $0$, want elk punt kan direct verbonden worden met een ander: er zijn daarvoor geen spiegelwanden nodig.

Het spiegelgetal van de middelste vorm in figuur 3 is $2$, want het 'lastigste geval' is het tweetal hoekpunten $A$ en $B$, dat vrij eenvoudig door twee spiegelingen ($45^{\rm o}$-lijnen) verbonden kan worden. Merk op dat de lichtstraal van hoekpunt $C$ naar hoekpunt $D$ niet mag: hij snijdt het verst naar binnen gelegen hoekpunt (rand) van de figuur. (Ook een lichtstraal die eindigt in een hoekpunt zoals $A$, $B$, $C$ of $D$ mag niet, want daarbij is geen terugkaatsende straal te bepalen.) Verder is het handig om te beseffen dat alleen randpunten bekeken hoeven te worden. Veel moeilijker te bewijzen is dat het spiegelgetal van de derde figuur maar liefst $9$ is. Ook dit is een zogeheten polyomino: een vorm met minstens één zijde aan elkaar geplakte vierkantjes.

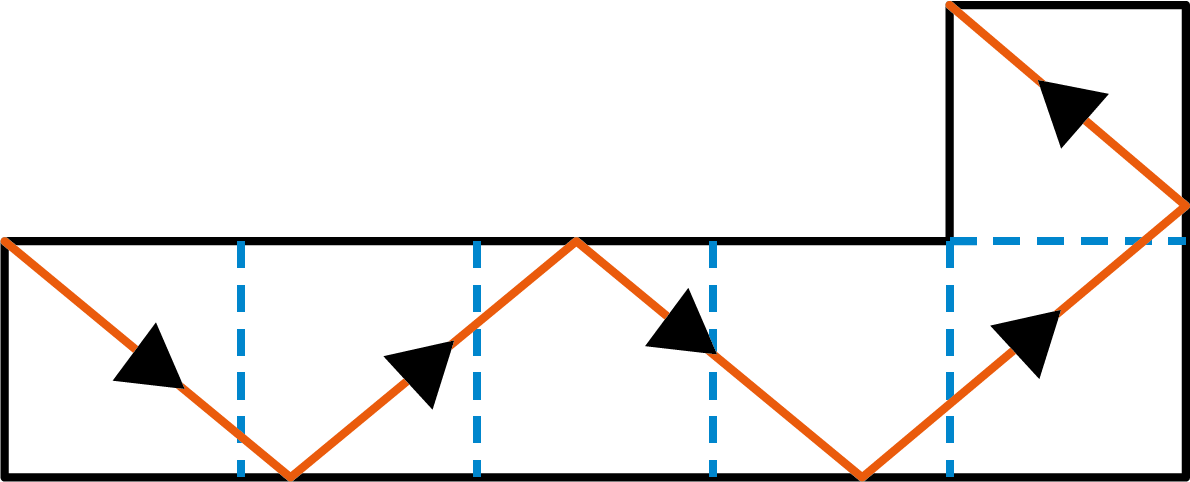
Nog een voorbeeld: het spiegelgetal van de polymino in figuur 4 (een 'hexomino', met dus zes vierkantjes) is $4$, getuige de twee 'moeilijkst' te verbinden punten en hun 'stralengang' (met richtingscoëfficiënt $-5/6$ dan wel $5/6$).

We beperken ons, in tegenstelling tot Tokarsky en Castro, tot polyomino's en hebben de volgende opgaven.

Opgave 1 Bepaal het spiegelgetal van Opgave 2 Bepaal het spiegelgetal van Opgave 3 Bedenk welk spiegelgetal nooit voorkomt bij polyomino's. Opgave 4 Bedenk een andere, niet-polynominovorm, waarbij het spiegelgetal uit opgave 3 wél optreedt.