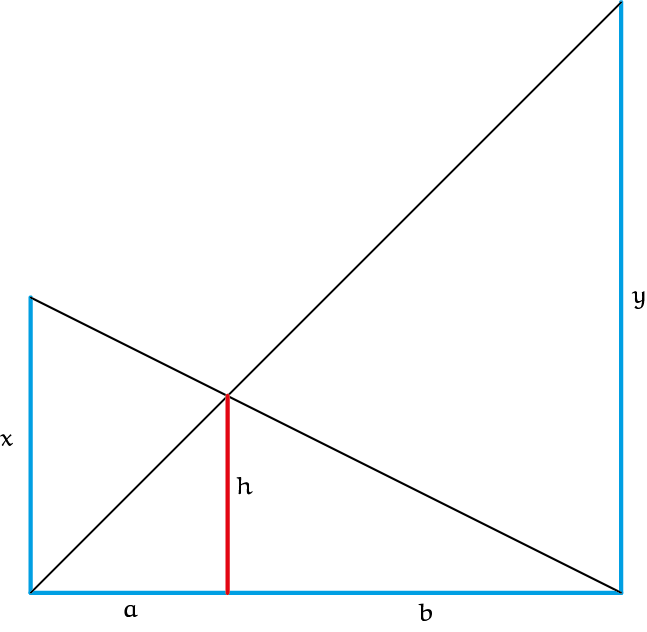
Stel de volgende situatie voor. Twee palen zijn verticaal geplaatst op een horizontaal stuk grond. De lengtes van de palen boven de grond zijn $x$ meter en $y$ meter met $x < y$. De palen zijn vervolgens met elkaar verbonden door touwen die lopen vanaf de top van elke paal naar de voet van de andere paal. De horizontale afstand tussen de twee palen is niet bekend maar het is nuttig om de twee delen van die afstand een naam te geven zoals in figuur 1. 

Opgave 1 Op welke hoogte $h$ kruisen de twee touwen elkaar tussen de twee palen? Het antwoord moet alleen in termen van $x$ en $y$ gegeven worden.  Hint: zoek twee gelijkvormige driehoeken.

Deze eerste constructie gebruikt veel touw en de twee toppen van de palen zouden verbonden kunnen zijn met een tweede constructie via een punt $S$ op de grond, zoals in figuur 2.

 

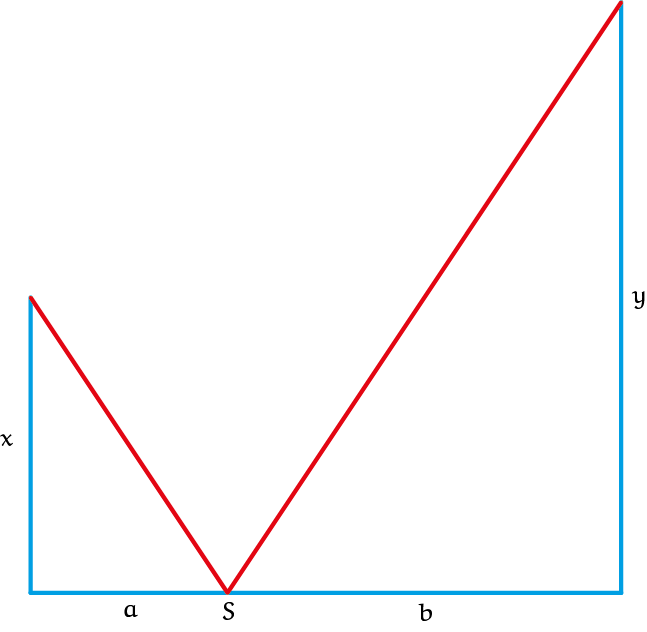
Opgave 2 Bewijs dat de plaatsing van punt $S$ op de voet van de lengte $h$ (uit figuur 1) de kortste totale lengte touw nodig heeft voor deze tweede constructie.

Het is natuurlijk ook mogelijk om de twee toppen van de palen rechtstreeks met elkaar te verbinden, zoals in figuur 3.

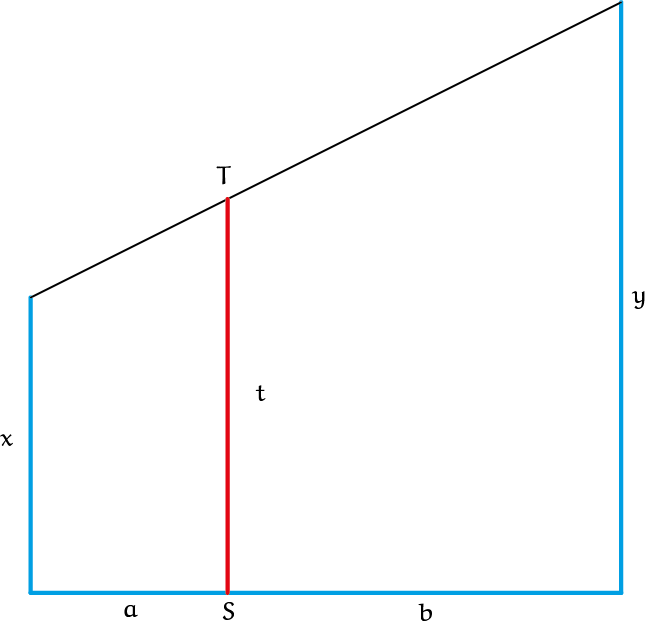
Opgave 3 Hoe hoog boven de grond (lengte $ST$) is het touw als we gaan meten vanaf de voet van de lengte $h$ (uit figuur 1)?

Blijkbaar levert het antwoord op opgave 3 een lengte tussen $x$ en $y$ in en dus een soort gemiddelde van $x$ en $y$. Laten we die $t$ noemen.

Opgave 4 Geef een bewijs dat $x < t < y$.

De twee bekendste gemiddelden van twee positieve getallen $x$ en $y$ zijn het rekenkundige gemiddelde $r = \frac{x+y}{2}$ en het meetkundige gemiddelde $m = \sqrt{xy}$. Het vinden van de bewijzen voor $x < r < y$,
$x < m < y$ en $m < r$ geeft een goede voorbereiding voor opgave 5.

Opgave 5 Bewijs nu dat $t < r$ en $t < m$. Opgave 6 Wat is de vergelijking die de variabelen $r$, $t$ en $m$ verbindt?

 

 

Bekijk oplossing