Opgave 1

Door gebruik te maken van gelijkvormige driehoeken krijgen we de volgende twee vergelijkingen:
$$\begin{cases} \frac{h}{y}&=\frac{a}{a+b} \\ \frac{h}{x}&=\frac{b}{a+b} \end{cases}$$.

Het optellen van deze vergelijkingen geeft $\frac{h}{y}+\frac{h}{x}=1$ en dus $h=\frac{xy}{x+y}$.

Opgave 2

Wederom via gelijkvormige driehoeken krijgen we $\frac{\left(y=\frac{xy}{x+y}\right)}{b}=\frac{\frac{xy}{x+y}}{a}$ en dus $\frac{xy+y^2-xy}{b(x+y)}=\frac{xy}{a(x+y)}$ en $\frac{y}{b}=\frac{x}{a}$. Dit bewijst dat de invalshoek en de reflectiehoek bij punt $S$ gelijk zijn en dit is een kenmerk van de kortste weg. Andere vormen van de vergelijking boven zijn $\frac{b}{a}=\frac{y}{x} \rightarrow 1+\frac{b}{a}=\frac{y}{x}+1 \rightarrow \frac{a+b}{a}=\frac{y+x}{x} \rightarrow \frac{a}{a+b}=\frac{x}{x+y}$. Dit kunnen we gebruiken voor het antwoord op opgave 3.

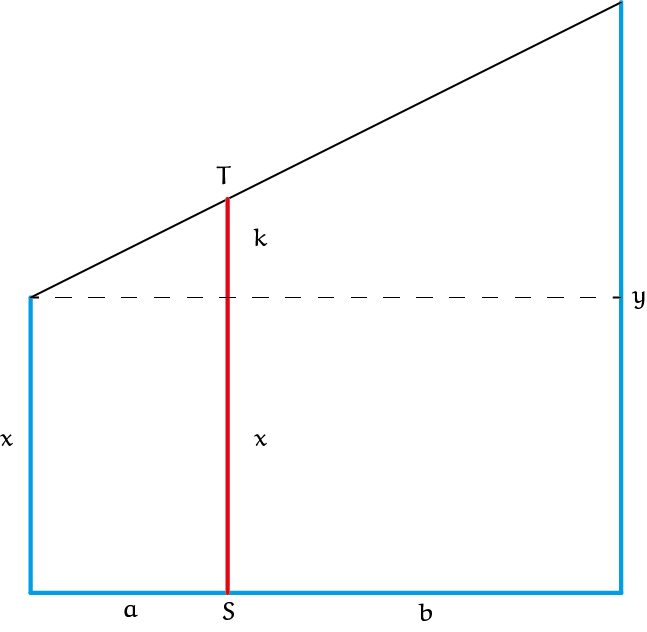
Opgave 3

Ook nu weer leveren gelijkvormige dirhoeken in de figuur ons $\frac{k}{y-x}=\frac{a}{a+b}=\frac{x}{x+y} \rightarrow k = \frac{xy-x^2}{x+y}$ en $x + k=\frac{2xy}{x+y}$.

Opgave 4

$x<y \rightarrow \frac{2y}{x+y}>1$ en $\frac{2x}{x+y}<1$. Dan is $\frac{2y}{x+y}\cdot x > x$ en $\frac{2x}{x+y}\cdot y < y$ en $x < t < y$.

Opgave 5

$0<(x-y)^2 \rightarrow 4xy<(x-y)^2+4xy \rightarrow 4xy<(x+y)^2\rightarrow \frac{2xy}{x+y}<\frac{x+y}{2}$ en dus $t<r$. Ook $0 < (x-y)^2 \rightarrow 4xy < (x-y)^2 + 4xy \rightarrow 4xy < (x+y)^2 \rightarrow 2\sqrt{xy}<(x+y)\rightarrow \frac{2\sqrt{xy}}{x+y}<1 \rightarrow \frac{2xy}{x+y} < \sqrt{xy}$ en dus $t<m$.

Opgave 6

De gevraagde formule is $$t=\frac{m^2}{r}.$$