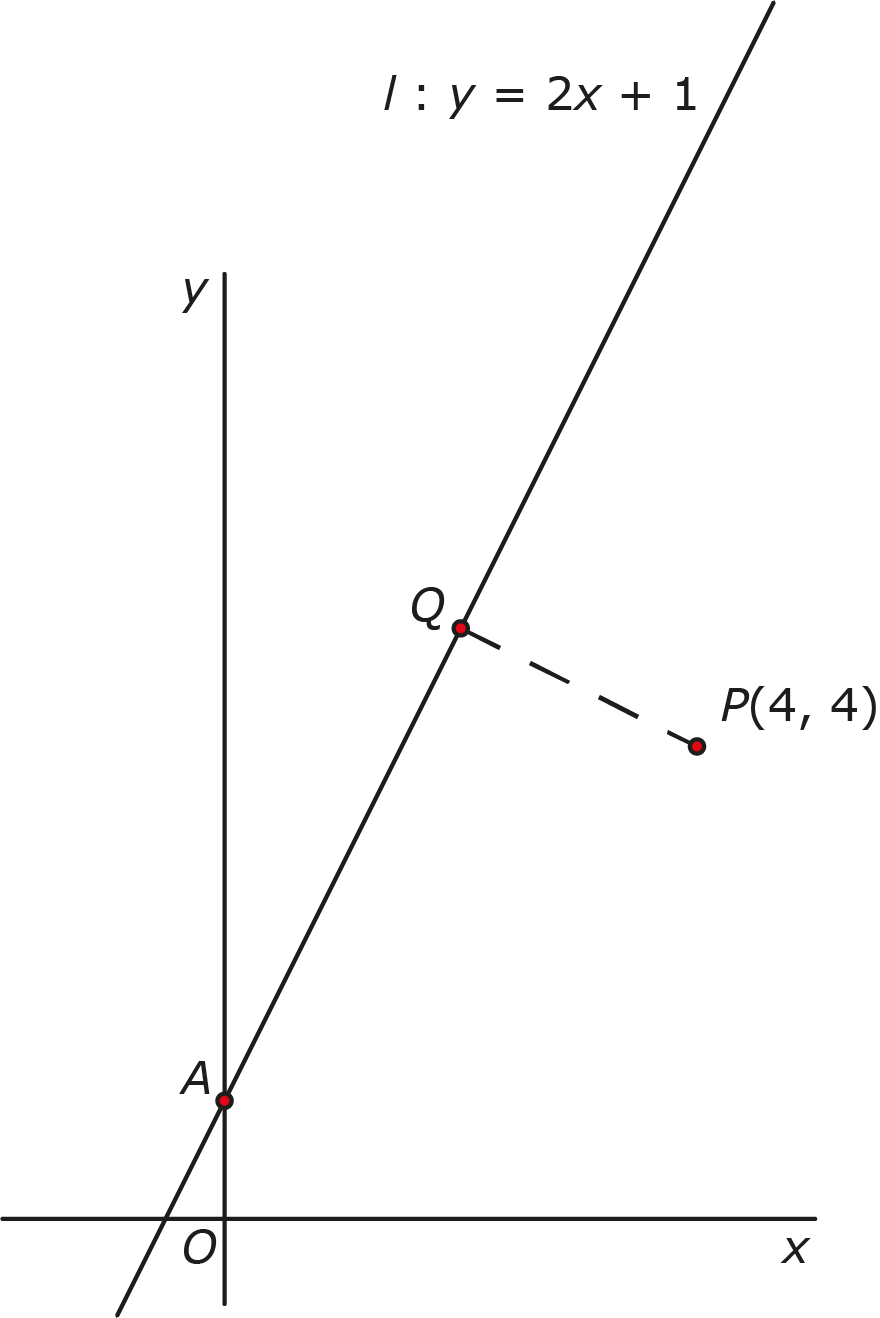
Figuur 1

1. Met de stelling van Pythagoras

We zouden kunnen beginnen met een punt op lijn $l$. De coördinaten van dat punt zijn $(x, 2x + 1)$. Voor de gewenste waarde van $x$ heeft de driehoek $APQ$ een hoek van $90^{\rm o}$. Met de stelling van Pythagoras kunnen we die $x$ vinden en dan de afstand $|PQ|$ weer met Pythagoras berekenen.

2. Met kruisende lijnen

Lijnstuk $PQ$ maakt deel uit van een lijn en de formule van deze lijn is te vinden met behulp van de richtingscoëfficiënt van $l$ en de coördinaten van punt $P$. Daarna kun je het snijpunt van deze twee lijnen vinden door hun vergelijkingen simultaan op te lossen en dan de afstand van $P$ tot $l$ te berekenen met Pythagoras.

3. Met gelijkvormige driehoeken

Als je bij punt $A$ begint dan kun je $A$ en $P$ verbinden met behulp van twee gelijkvormige driehoeken zoals de rode driehoeken in figuur 2. Nu leveren de coördinaten van $A$ en $P$ en de gelijke verhoudingen in de twee driehoeken een formule voor $x$ en de afstand tussen $P$ en $l$.

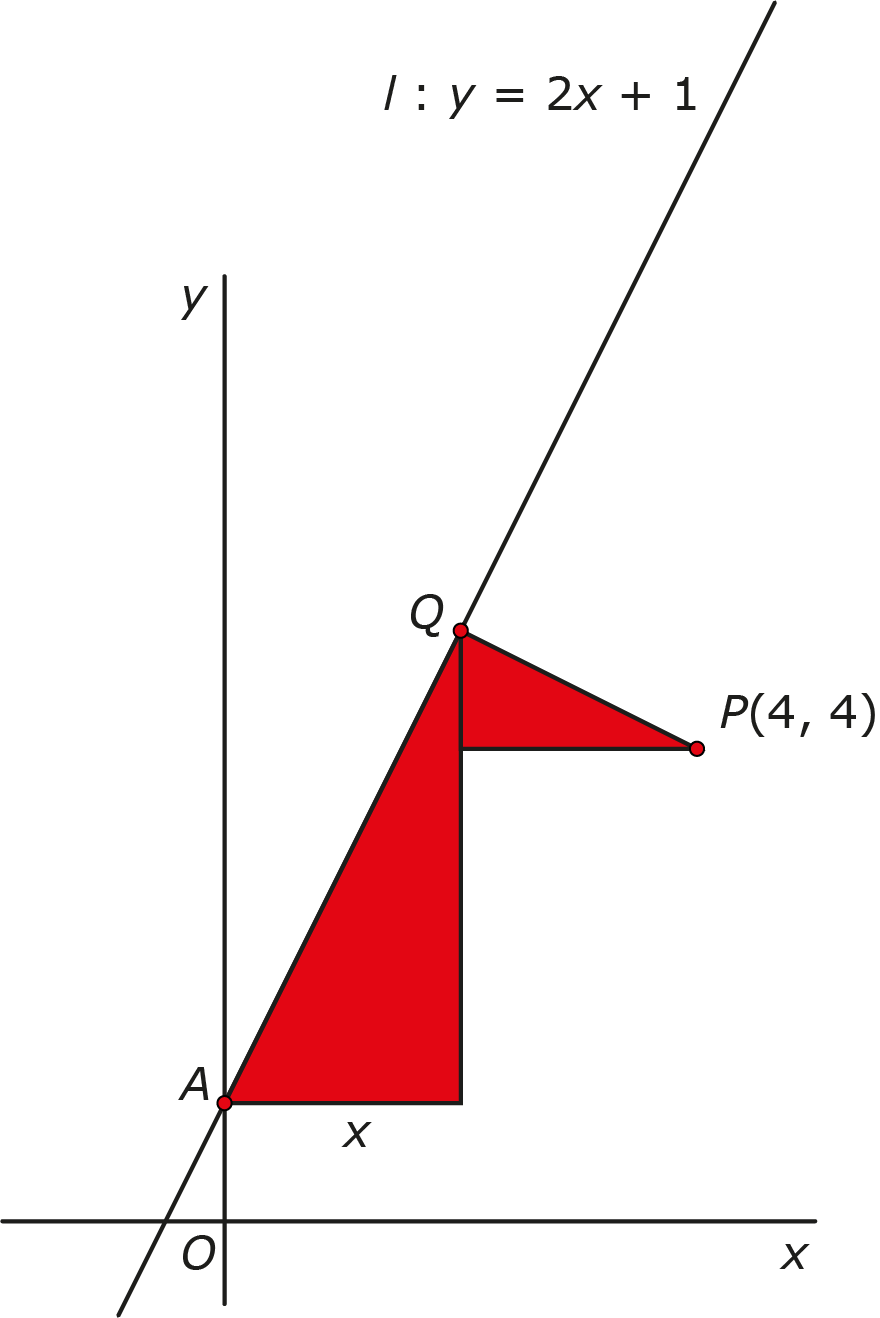
Figuur 2

4. Met een afstandsfunCtie

Ieder punt $(x, 2x + 1)$ op lijn $l$ heeft een afstand van $P$ die uit te drukken is als de waarde van een functie van $x$. De afgeleide van deze functie is nul voor de gewenste waarde van $x$.

5. Met de hoogte van een driehoek

Teken een verticale lijn door punt $P$ zoals in figuur 3. Deze lijn snijdt $l$ in punt $R$. Nu is de oppervlakte van driehoek $APR$ te vinden door te integreren. Deze oppervlakte is ook te berekenen met de lengte van $AR$ en de afstand $|PQ|$.

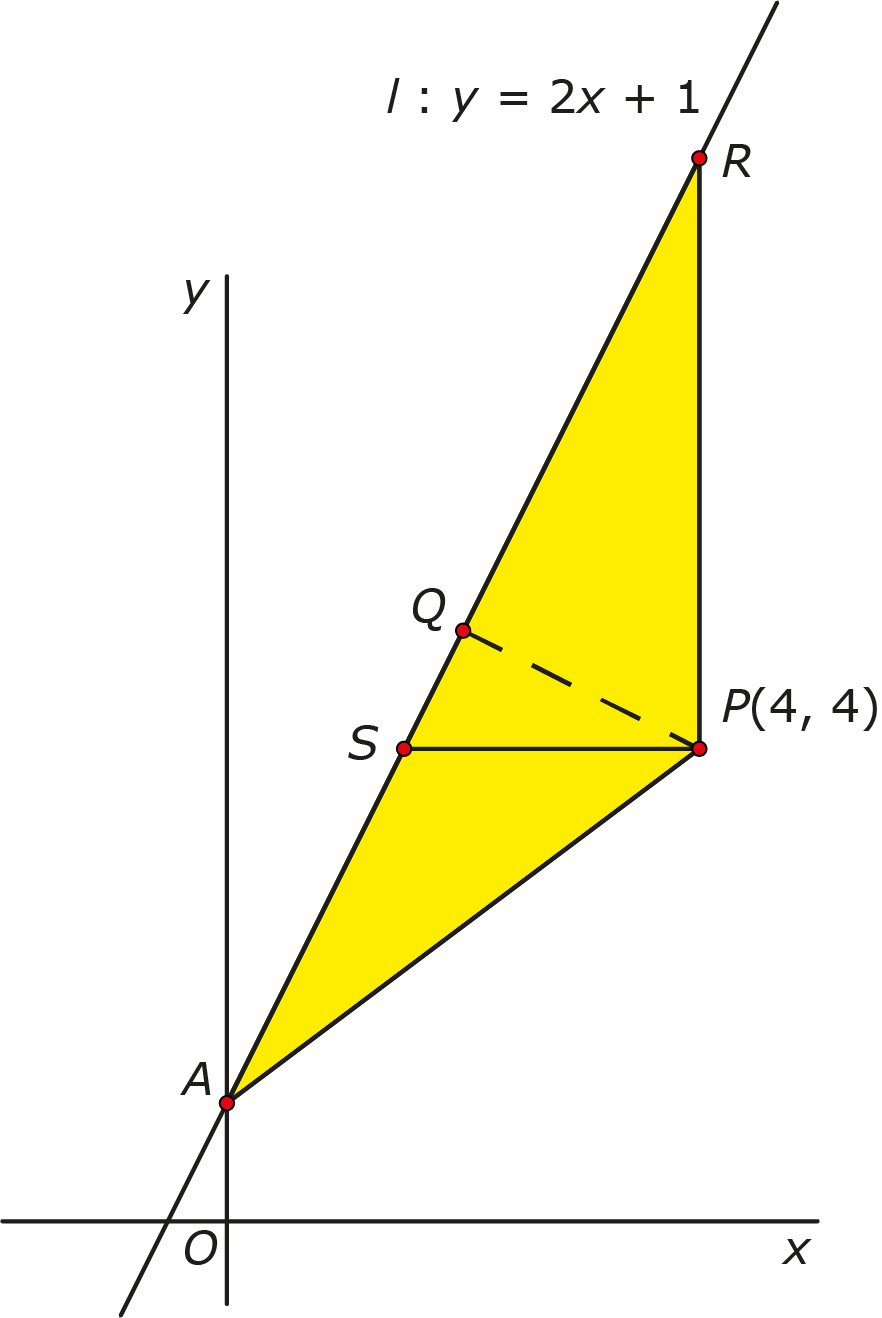
Figuur 3

6. Weer met een driehoek maar dan anders?

Is integreren niet je ding? Dan kun je $AP$ vervangen door een horizontaal lijnstuk $PS$ en weer op dezelfde manier de afstand $|PQ|$ berekenen.

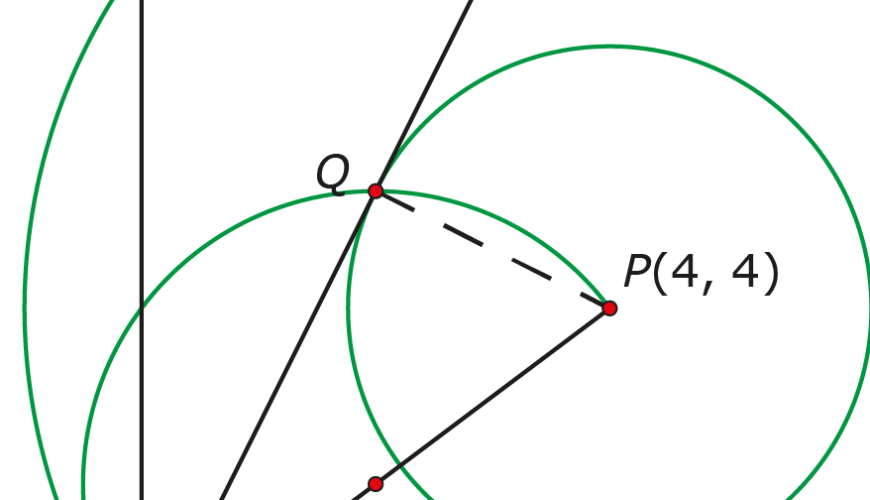
Cirkels zijn zo rond als wat en toch zijn er veel rechte hoeken te vinden die leiden naar de afstand van $P$ tot $l$. In figuur 4 zijn drie cirkels afgebeeld.

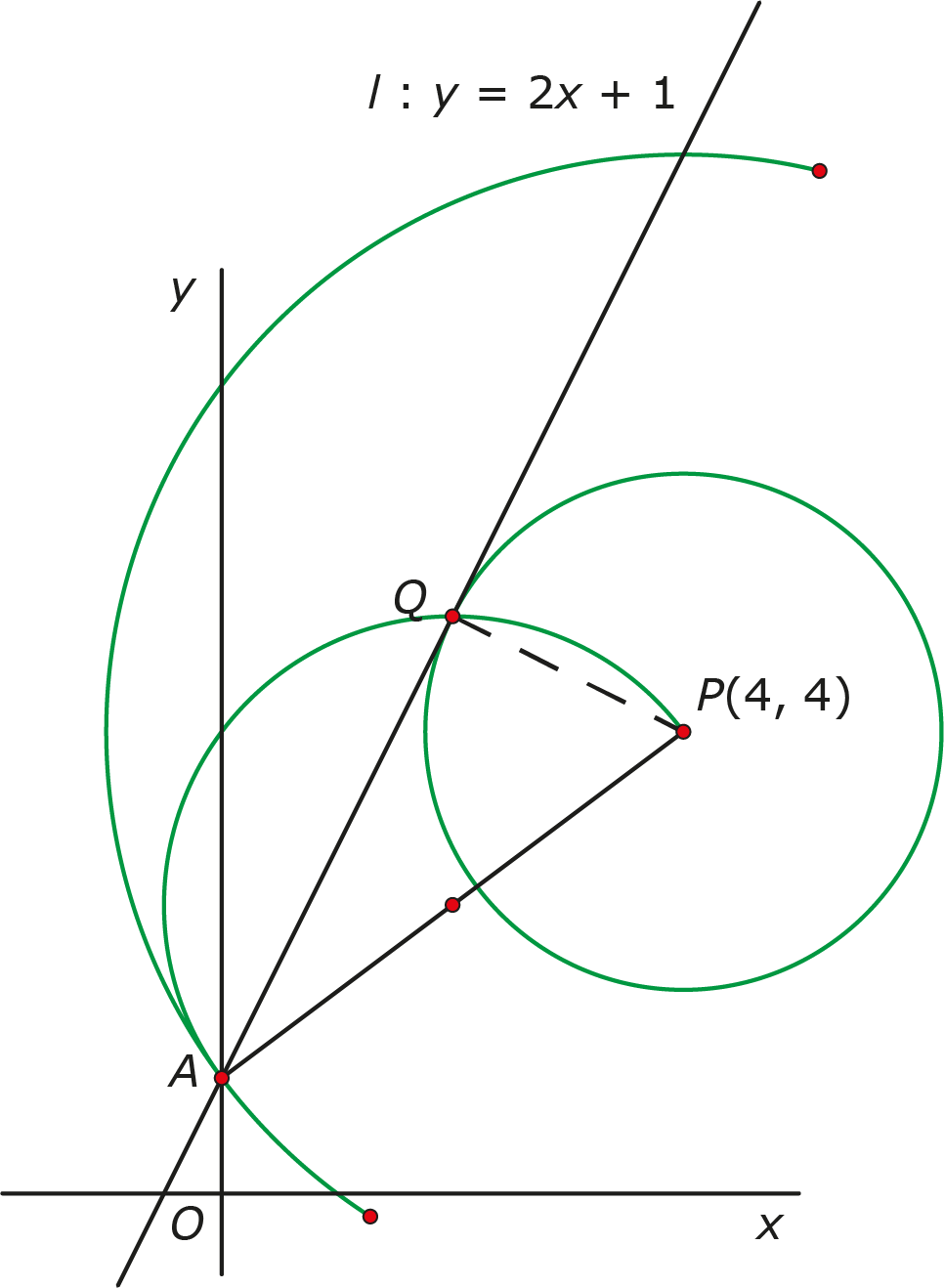
Figuur 4

7. Met de koordenstelling

Een cirkel met $P$ als middelpunt en $AP$ als straal snijdt lijn $l$ in twee punten. Halverwege deze twee punten is het punt op $l$ met de kleinste afstand tot $P$.

8. Met de stelling van Thales

Een cirkel met $AP$ als diameter snijdt $l$ op punt $A$ en op het gewenste punt $Q$.

9. Met de disCriminant

Een cirkel met middelpunt $P$ raakt lijn $l$ in het juiste punt als de cirkel en lijn maar één gezamenlijke oplossing hebben. Dan is de discriminant gelijk aan $0$.

In figuur 5 zijn twee eenheidsvectoren te vinden; dit zijn vectoren met lengte $1$. De vector $\varphi$ loopt parallel met $l$ en de vector $\vartheta$ staat loodrecht op $l$.

10. Met veCtoren en sCalair produCt

$Q$ is het gezochte punt op $l$. $AQ$ is de projectie van $AP$ op $l$ en deze projectie is te berekenen als het scalaire product van $\varphi$ en vector $\overrightarrow{AP}$. Nu kennen we de lengtes van zijden $AQ$ en $AP$ en is $PQ$ als derde zijde van rechthoekige driehoek $APQ$ met Pythagoras te berekenen.

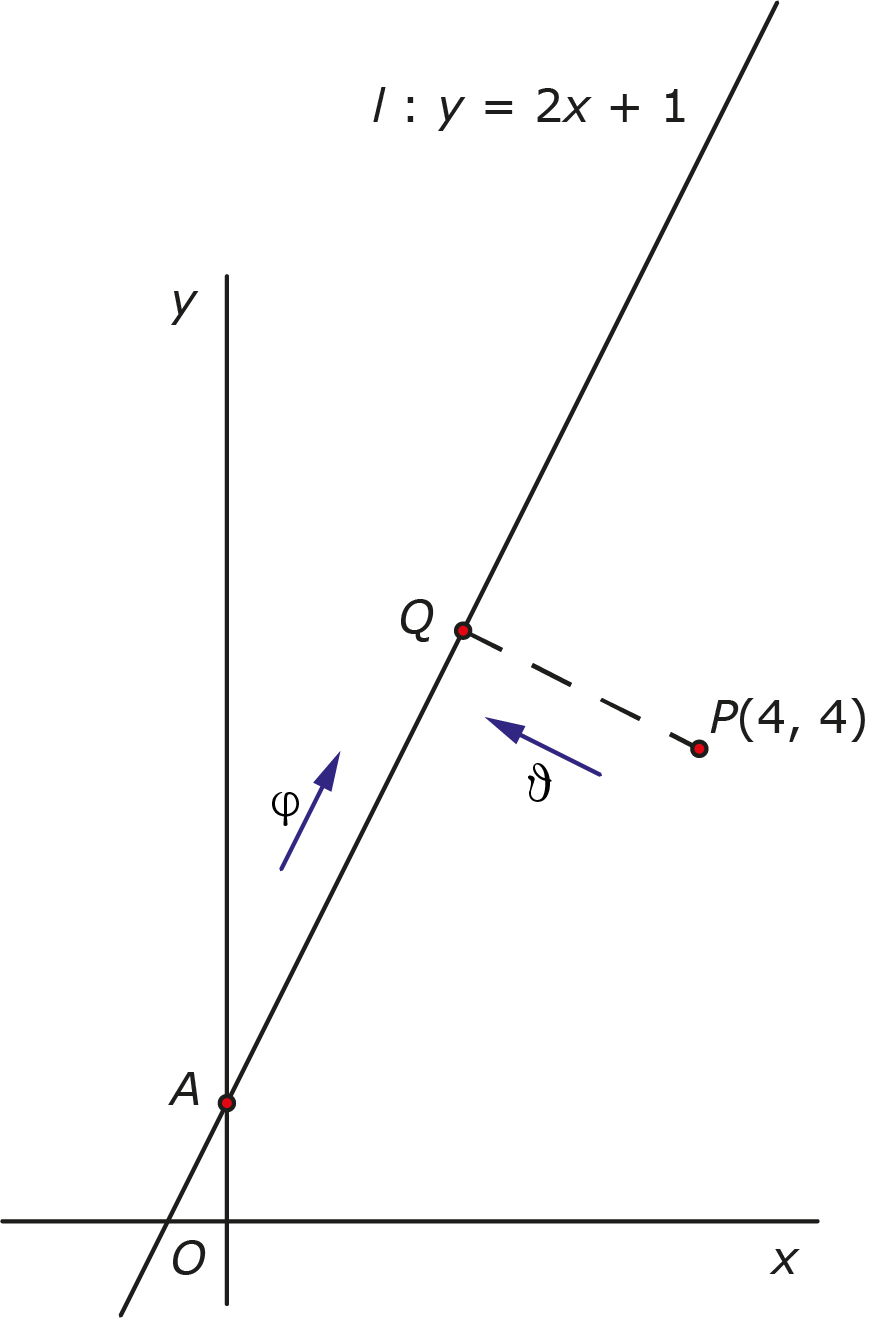
Figuur 5

11. Met veCtoren vanuit de oorsprong

De tweede vector methode begint op de oorsprong $O$. Vector $\overrightarrow{OP}$ brengt ons naar punt $P$ van waaruit we verder vertrekken met vector $\overrightarrow{PQ}$ naar punt $Q$. Vector $\overrightarrow{PQ}$ is een langere of kortere versie van vector $\vartheta$ en dus te beschrijven als $\mu \cdot \vartheta$ waar $\mu$ één of ander getal is. Het punt $Q$ dat we op zo’n manier bereiken heeft coördinaten die een oplossing vormen voor de vergelijking van lijn $l$. Dit levert een formule op voor de waarde van $\mu$, en $|\mu|$ is de afstand van $P$ tot $l$.

Al deze verschillende berekeningen geven het antwoord voor één concreet geval. Voordat we over een stelling kunnen praten moeten wij een bewijs vinden voor een algemene formule. 

In een volgende nummer van Pythagoras zullen we kijken naar een paar bewijzen en ook zien waar dit verder naar toe leidt.

Bekijk oplossing