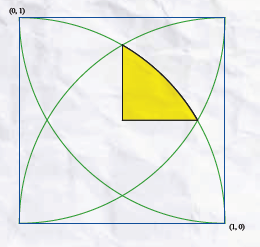
Vierkel Antwoorden
Deze vierkel heeft een oppervlakte van $1-\sqrt{3}+\frac{\pi}{3}$. Vier wegen die naar het antwoord leiden zijn:
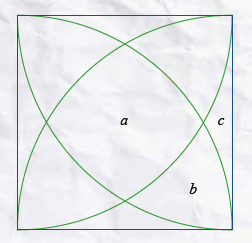
Meetkunde
Het combineren van het patroon onder levert de oppervlakte $(\frac{\sqrt{3}}{4} − \frac{\pi}{12})$ en dus het antwoord.
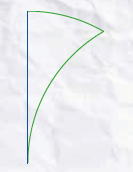
Algebra
Het benoemen van 3 oppervlaktes levert een stelsel van vergelijkingen en dus het antwoord.
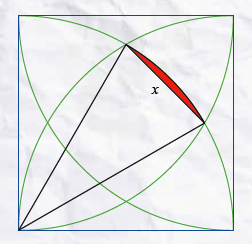
Goniometrie
De cosinusregel en het berekenen van het rood gekleurde oppervlak leiden tot het antwoord.
$x^2 = 2−\sqrt{3}$ rode oppervlak $= \frac{\pi}{12} −\frac{1}{4}$.
Integraalrekening
opp $= 4 \int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}} \left( \sqrt{1-x^2}-\frac{1}{2}\right)dx$