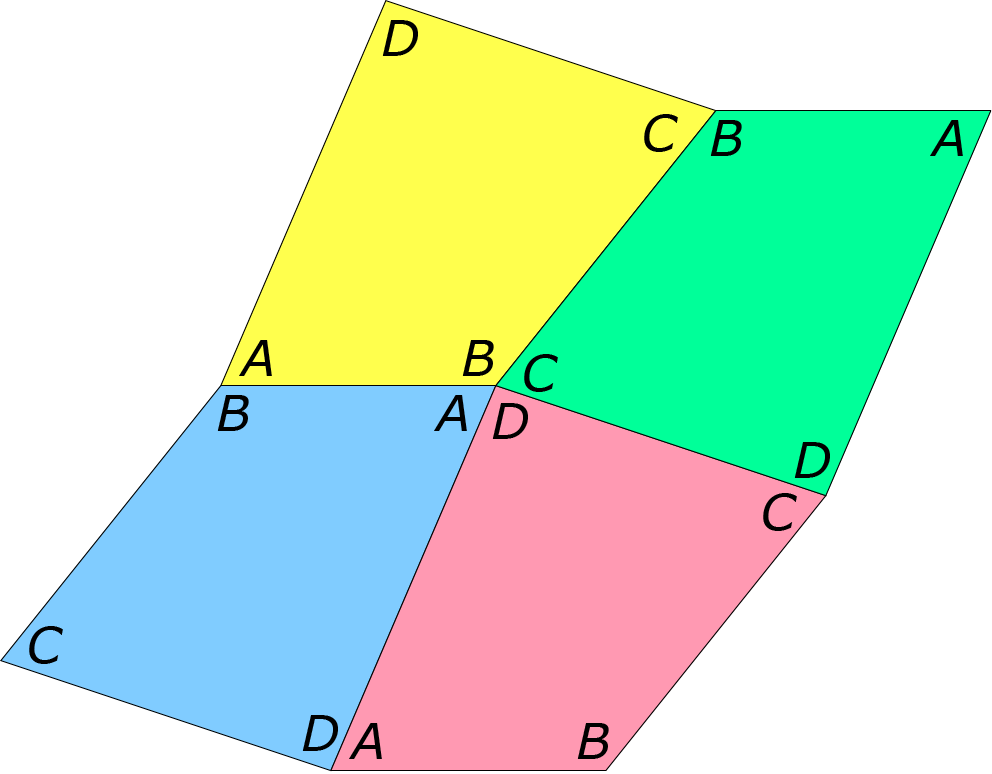
Een vlakvulling is een oneindig patroon dat steeds weer terugkomt, opgebouwd uit dezelfde basisfiguren. Laten we beginnen met een willekeurige vierhoek (figuur 1a).

De vraag is: kun je met een willekeurige vierhoek altijd een vlakvulling maken? Ja zeker! Je ziet de vlakvulling al staan (figuur 1b). En het gaat nog eenvoudig ook! In figuur 1c zijn vier vierhoeken getekend die in één punt samenkomen. In elk hoekpunt komen de vier verschillende hoeken samen. Een vierhoek met zijn buur deelt steeds een gelijke zijde.

De vraag is of het ook net zo eenvoudig is om met driehoeken een vlakvulling te maken. Dat is inderdaad het geval. We nodigen je uit om daar zelf mee te experimenteren!

Vlakvullingen met vijfhoeken zijn een compleet ander verhaal, een verhaal dat hieronder wordt verteld...

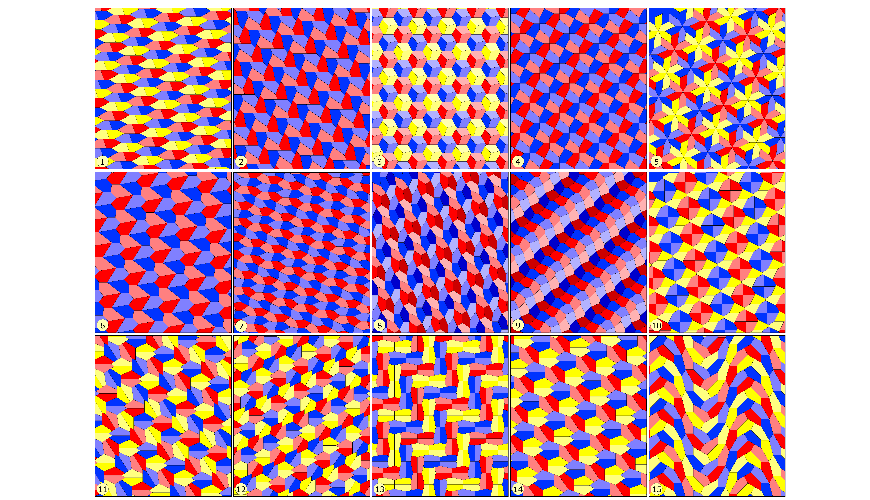
In elk van de 15 plaatjes bovenaan zien we zeer regelmatige vlakvullingen, waarbij steeds één stempeldeel wordt gebruikt in de stempel. Bovendien zijn er twee verschuivingen (translaties) in verschillende richtingen te vinden. Het stempeldeel is steeds een vijfhoek, die convex is, d.w.z. de vijf hoeken zijn alle kleiner dan $180^{\rm o}.$

Elk plaatje staat voor een serie (type). Het eerste type vlakvulling omvat ook het huisje (1^S) en de Cairo-betegeling (4^S), genoemd naar Cairo, omdat daar die betegeling veel wordt gebruikt.

Een aantal van de vlakvullingen zijn al geruime tijd bekend. Op Wikipedia staat een goed overzicht van wanneer de verschillende types werden ontdekt:

Type	Jaar	Ontdekker(s)
1, 2, 3, 4, 5	1918	Reinhardt
6, 7, 8	1968	Kershner
10	1975	James
9, 11, 12, 13	1977	Rice
14	1985	Stein
15	2015	Mann, McLoud, Derau

Dit zijn tevens alle types vlakvullingen met vijfhoeken. In 2017 werd door Rao bewezen dat er geen andere types bestaan.

Het gaat te ver om hiervan een bewijs te geven. Maar ik kan proberen een tipje van de sluier op te lichten door te bewijzen dat er slechts vier driehoeken bestaan waarmee je een vlak kunt vullen op een dusdanige manier dat ongelijke hoeken nooit bij elkaar samenkomen.

We gaan uit van een driehoek met hoeken $\alpha$, $\beta$ en $\gamma.$ Uiteraard geldt voor een driehoek dat $\alpha + \beta + \gamma = 180^{\rm o}.$ Aangezien ongelijke hoeken nooit in een hoekpunt mogen samenkomen moet gelden dat een geheel aantal hoeken samen $360^{\rm o}$ zijn. We introduceren gehele getallen $a,$ $b$ en $c$ zo dat $a\alpha = 360^{\rm o},$ $b\beta = 360^{\rm o}$ en $c\gamma = 360^{\rm o}.$ We elimineren nu $\alpha$, $\beta$ en $\gamma:$

$$\frac{360^{\rm o}}{a} + \frac{360^{\rm o}}{b} + \frac{360^{\rm o}}{c} = 180^{\rm o}.$$

Ten slotte delen we door $360^{\rm o}.$ We vinden de vergelijking

$$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{2}.$$

We zoeken nu naar alle mogelijke oplossingen in positieve getallen $a,$ $b$ en $c$ voor deze vergelijking. We vinden:

$a$	$b$	$c$
3	7	42
3	8	24
3	9	18
3	10	15
3	12	12	*(1)
4	5	20
4	6	12	*(2)
4	8	8	*(3)
5	5	10
6	6	6	*(4)

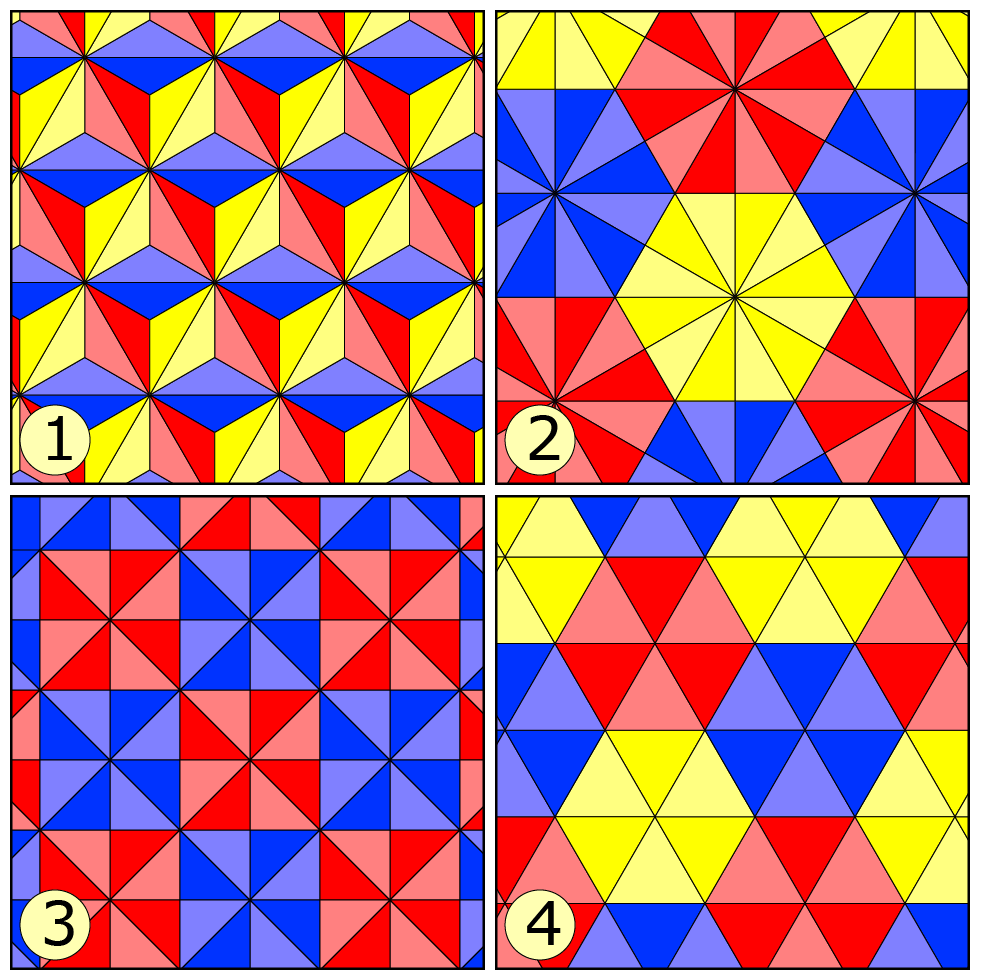
Van bovengenoemde mogelijkheden blijken slechts 4 mogelijkheden ook echt te kunnen voorkomen (in regelmatige patronen), zie figuur 2.