[oOO]

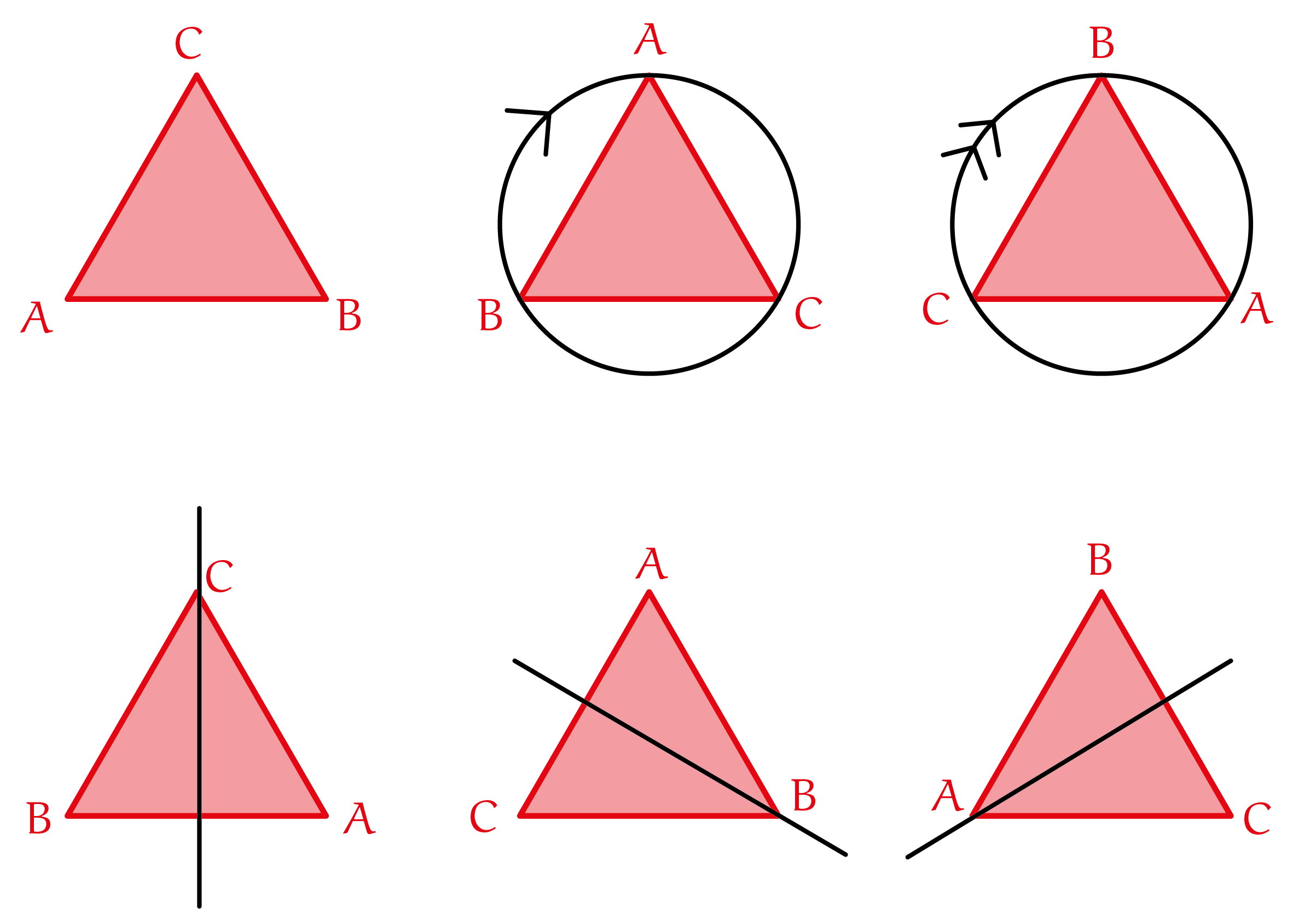
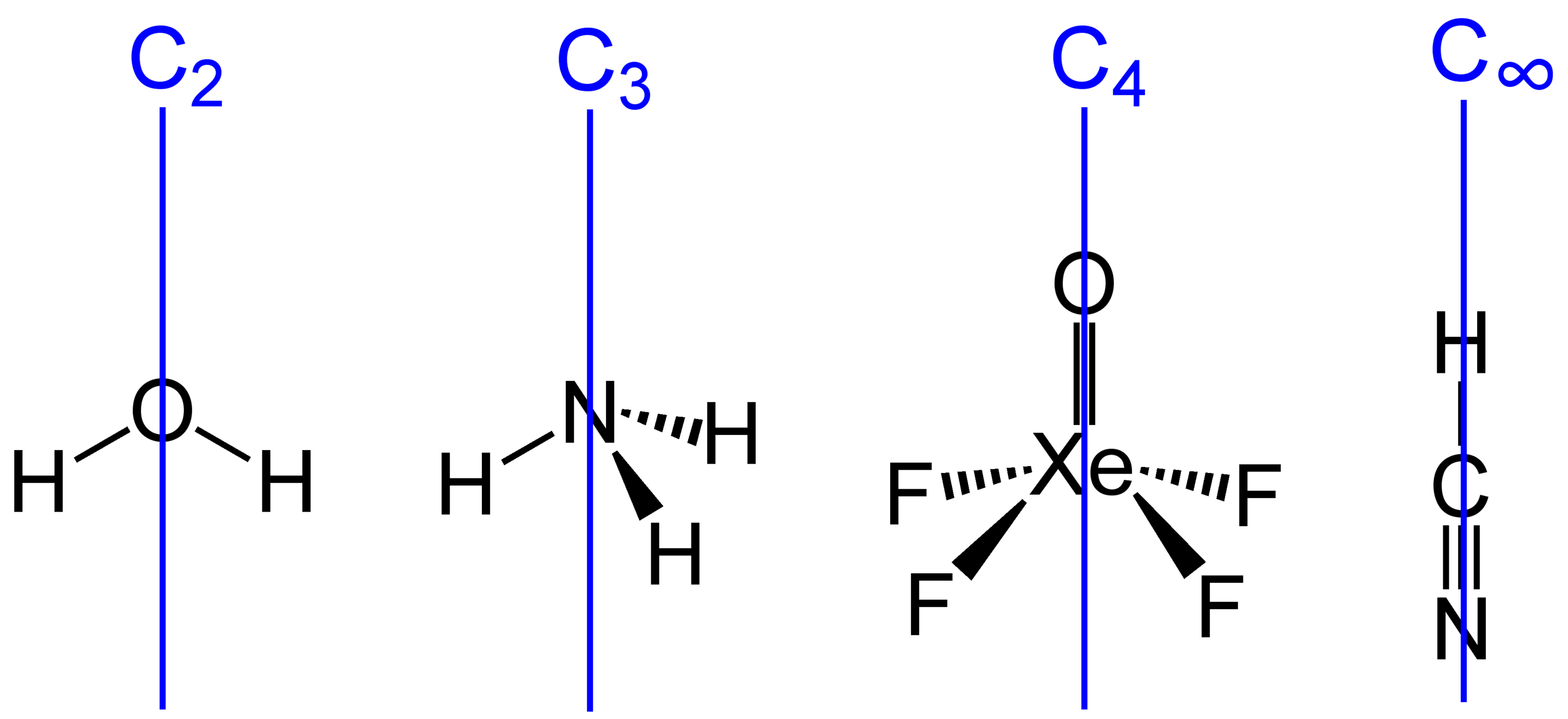
Wiskunde van symmetrie: groepentheorie

Wat houdt groepentheorie ongeveer in? We beginnen met een voorbeeld. 
Op hoeveel verschillende manieren kun je een gelijkzijdige driehoek draaien of spiegelen zodat de resulterende driehoek samenvalt met de originele? Je kunt hem draaien over $0^{\rm o}$ (de ’identiteit’), $120^{\rm o}$ of $240^{\rm o}$ rond zijn zwaartepunt en spiegelen in drie verschillende assen. In totaal geeft dit zes ‘transformaties’ waarna de driehoek er hetzelfde uitziet. Veel moleculen, die samengesteld zijn uit verschillende atomen, hebben dit soort symmetrieën. De moleculaire symmetrie (zie figuur 1) geeft aan hoe vaak een molecuul geënverteerd, gedraaid, gespiegeld en gedraaispiegeld kan worden, met allerlei gevolgen voor de orbitaalstructuur, reactiviteit en fysische eigenschappen zoals het dipoolmoment.

$\color{red}{Figuur\ 1 -{}}$ Symmetrieën van een gelijkzijdige driehoek; draaisymmetrieën van vier moleculen met de draaias: water, ammoniak, xenonoxytetrafluoride en waterstofcyanide

Een verzameling objecten, met bewerkingen zoals draaiing en spiegeling, of optelling of vermenigvuldiging, vormt als de bewerking aan vier regels voldoet een ‘groep’. Objecten hoeven geen figuren te zijn men. De gehele getallen met als bewerking ‘optelling’ vormen bijvoorbeeld een groep. Het bestuderen van symmetrieën wordt in de wiskunde gedaan in de groepentheorie. Men bestudeert symmetrie binnen allerlei mogelijke wiskundige structuren en groepen kunnen heel groot en ingewikkeld zijn. Om ze beter te kunnen begrijpen hebben wiskundigen ‘representaties’ bedacht, waarmee groepen kunnen worden voorgesteld door $n\times n$ inverteerbare matrices. Matrices zijn veel makkelijker ommee te werken en te begrijpen. Dus je kunt willekeurige groepen beter begrijpen door ze als een matrixgroep voor te stellen. In de theoretische fysica spelen matrixgroepen een belangrijke rol. Een aantal decennia geleden is de classificatie van een specifiek soort symmetriegroepen - eindige enkelvoudige groepen - voltooid. Daarvan zijn er 26 zogenaamde ‘sporadische groepen’. De grootste van deze sporadische groepen is de ‘monstergroep’. En deze speelt een rol in de oudst bekende maneschijn, waardoor Cheng bij haar ontdekking werd ge¨ınspireerd.

Van monster naar j-functie via maneschijn

De monstergroep heeft $808\,017\,424\,794\,512\,875\,886\,459\,904\,961\,710\,757\,005\,754\,368\,000\,000\,000$ elementen. Dat is erg groot, ongeveer $8 × 10^{53}$ elementen! Ter vergelijking: het aantal atomen op aarde wordt geschat op $10^{50}$. Gelukkig is er de representatietheorie, waardoor het onderzoek ernaar kan worden beperkt tot bepaalde eigenschappen. Al toen wiskundigen nog niet zeker wisten of de monstergroep bestond, probeerden ze hem te begrijpen m.b.v. representaties. Ze wisten daardoor dat de monstergroep, als hij bestond, in bepaalde dimensies op een speciale manier zou werken. De kleinste van deze dimensies waren $1$ en $196\,883$. In 1978 merkte John McKay bijna per toeval op dat de eerste belangrijke coëfficiënt van de $j$-functie, $196\,884$, gelijk is aan de som van de eerste twee speciale dimensies. Nadat John Thompson ontdekte dat de tweede coëfficiënt van de $j$-functie, $21\,493\,760$, gelijk is aan de som van de eerste drie speciale dimensies van het monster: $1 + 196\,883 + 21\,296\,876$, vermoedden wiskundigen Conway (o.a. bekend van de Game of Life) en Norton dat hier iets bijzonders aan de hand was, en ze publiceerden hun vermoeden in een artikel ‘Monstrous moonshine’. Pas nadat Griess de monstergroep eindelijk had kunnen construeren bewees Borcherds in 1992 dat het vermoeden juist is, en dat de brug tussen beide onverwante gebieden wordt gevormd door snaartheorie. In deze theorie worden elementaire deeltjes voorgesteld door trillende snaren. En de $j$-functie beschrijft de trillingen in een specifiek snaartheoriemodel, terwijl de monstergroep de symmetrieën van de ruimtetijd beschrijft waarin deze snaren wonen. Zie figuur 3 voor een schematische voorstelling van de brug.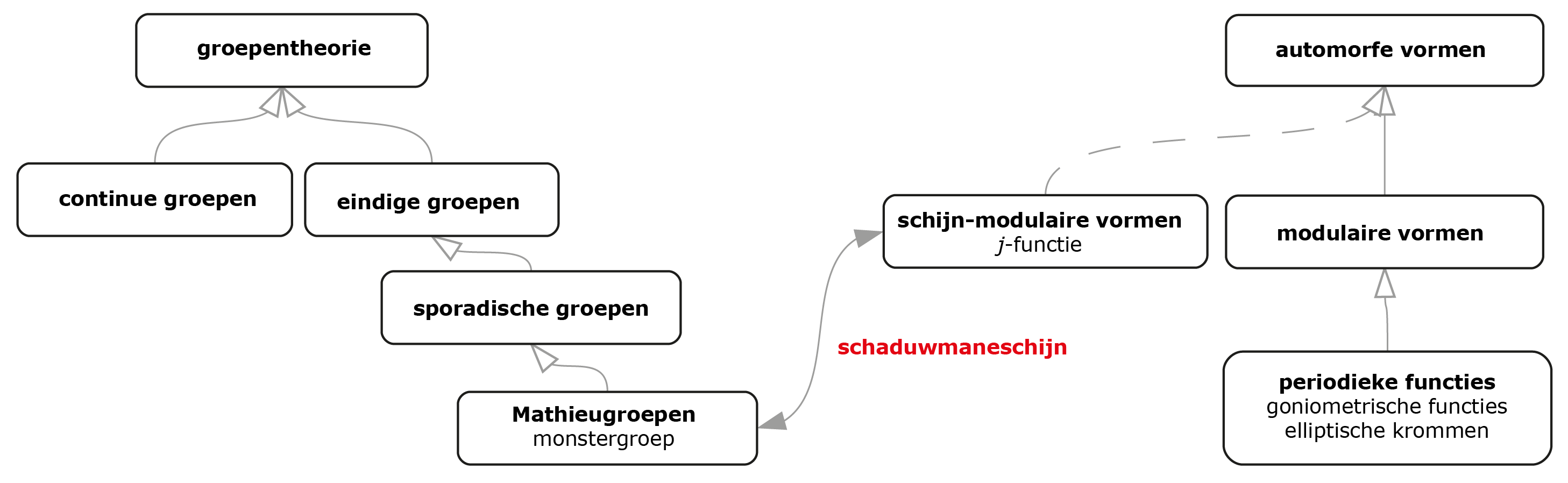

Grappig feitje: De monstergroep heeft 19 andere vrienden binnen de sporadische groepen, die samen een blije familie vormen. Een ander lid van de familie is het babymonster!

Toen Miranda Cheng in 2010 een artikel las over een vreemd verband tussen $K3$-oppervlakken en de sporadische Mathieugroep $M_{24}$ dacht zij dat er hier wellicht ook sprake zou zijn van een soort maneschijn. Een veel relevantere dan de vorige, omdat de $K3$-oppervlakken die hier de brug tussen de dimensies van een symmetriegroep en de coëfficiënten van een speciale functie zouden vormen, worden gebruikt als mogelijk model voor ‘echte’ ruimte-tijd. Dit in tegenstelling tot de snaartheorie die de link vormde tussen de monstergroep en de $j$-functie. Na haar eerste ontdekking vond Cheng met collega’s John Duncan en Jeff Harvey uiteindelijk sterke aanwijzingen voor het bestaan van 23 nieuwe soorten maneschijn! Deze noemden zij ‘schaduwmaneschijn’ (umbral moonshine).

Gezocht: theorie voor zwaartekracht op zeer kleine schaal

Zoals gezegd, beschrijft de $j$-functie trillingen in een bepaald snaartheoriemodel. Waar gaat snaartheorie over? Daar gaan we nu op in. Alle processen in dit heelal worden bepaald door vier fundamentele krachten in de natuurkunde: de elektromagnetische kracht, de sterke en zwakke kernkracht en de zwaartekracht. Voor de zwaartekracht is er Newtons beschrijving voor lage snelheden en massa’s en Einsteins relativiteitstheorie voor hoge snelheden en grote massa’s. Zwaartekracht is continu, maar de overige drie krachten zijn discreet: de zwakke en sterke kernkracht en elektromagnetische kracht worden het best beschreven m.b.v. deeltjes, en kwantumtheorieën voor hun gedrag. Volgens de huidige stand van zaken kunnen de laatste drie wisselwerkingen zo tezamen worden beschreven door het ‘standaardmodel van de deeltjesfysica’.

Vele onderzoekers zoeken naar een ‘theorie van alles’. Ze proberen de de theorie van zwaartekracht op grote schaal en hoge snelheden te verenigen met de kwantumtheorieën voor krachten op zeer kleine schaal, opdat zij ook zwaartekracht op zeer kleine schaal kunnen bestuderen, zoals bij zwarte gaten vlak na de oerknal.

Een aantal voorbeelden van kwantumzwaartekrachtstheorieën zijn causale dynamische driehoeksmeting (causal dynamical triangulation, CDT), de luskwantumzwaartekracht die inmiddels op basis van ESA waarnemingen verworpen is, twistortheorie en snaartheorie. Voor geen van de theorieën is er experimenteel bewijs, maar zolang alles overeen lijkt te komen met experimenten kunnen we theorie¨en gebruiken die we wel hebben gevonden. De snaartheorie is een interessante kandidaat voor de ‘theorie van alles’ en de gebruikte wiskunde voor de theorie bekoort vele wiskundigen en natuurkundigen, onder wie Cheng.

Volgens een versie van snaartheorie zijn er 10 ruimtetijd-dimensies. Hiervan nemen we er 4 waar: ruimte in 3 dimensies en de tijdsdimensie. Volgens deze snaartheorie moeten de overige 6 dimensies ergens ‘opgerold’ zijn. Hiervoor hebben onderzoekers een model nodig dat niet te ingewikkeld en niet te simpel is. Het $K3$-oppervlak komt hiervoor in aanmerking (zie figuur 3). In de $K3$-versie van snaartheorie, welke ten grondslag zou liggen aan de 23 vermoede verbanden, heeft ruimtetijd de meetkunde van een 4-dimensionaal $K3$-oppervlak. Volgens Cheng is dit relevant voor bijvoorbeeld zwarte gaten. Zij werkte al tijdens haar promotie aan vragen over zwarte gaten en samen met o.a. Sarah Harrison aan $K3$-oppervlakken. Met een dergelijke theorie kun je bijvoorbeeld de vraag proberen te beantwoorden wat er met kwantuminformatie gebeurt als die in een zwart gat valt.

Een driedimensionale voorstelling van een $K3$-oppervlak. Bron: Wikipedia

Hoewel de maneschijn veelbelovend is, zijn er ook nog veel mysteries. De belangrijkste zijn de ontbrekende modules met de juiste dimensies in de kandidaat symmetriegroepen: er zijn verschillende voorbeelden van schaduw-maneschijnmodules die wel door onderzoekers zijn gevonden, maar een algemene constructie ontbreekt nog steeds. Zelfs de benodigde module voor de $M_{24}$ maneschijn die de bron was van Chengs vermoeden is nog steeds niet ontdekt.

Verder lezen 

Natalie Wolchover, "Moonshine master toys with string theory".

Marcus du Sautoy, Het symmetriemonster, Uitgeverij Nieuwezijds.

Roel Andringa-Boxum, Schitterende Symmetrieën, Epsilon Uitgaven.