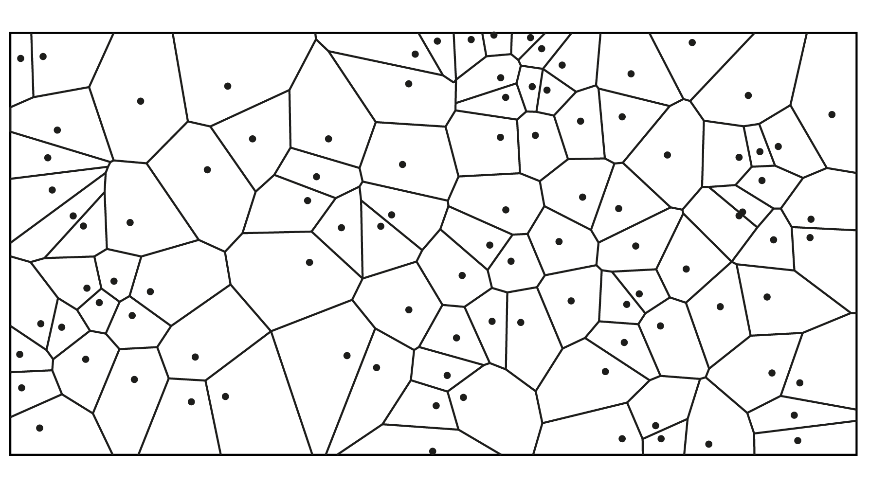
Een Voronoidiagram is een opdeling van het platte vlak in veelhoeken. Die opdeling wordt bepaald door de afstand tot een aantal gegeven punten in dat vlak. Elke veelhoek 'rondom' zo'n punt is dan het gebied van punten waarvoor de afstand tot dat ene punt korter is dan de afstand tot elk ander punt. Het diagram is vernoemd naar de Oekraïense wiskundige Georgy Voronoi (1816-1908). De veelhoeken in een Voronoidiagram zijn altijd convex, dat wil zeggen: zonder gaten of instulpingen. Voronoidiagrammen worden gebruikt in vele uiteenlopende gebieden, van informatica tot biologie, of bij het vinden van bijvoorbeeld het dichtstbijzijnde benzinestation of ziekenhuis. In figuur 1 staat een voorbeeld van een Voronoidiagram.

 

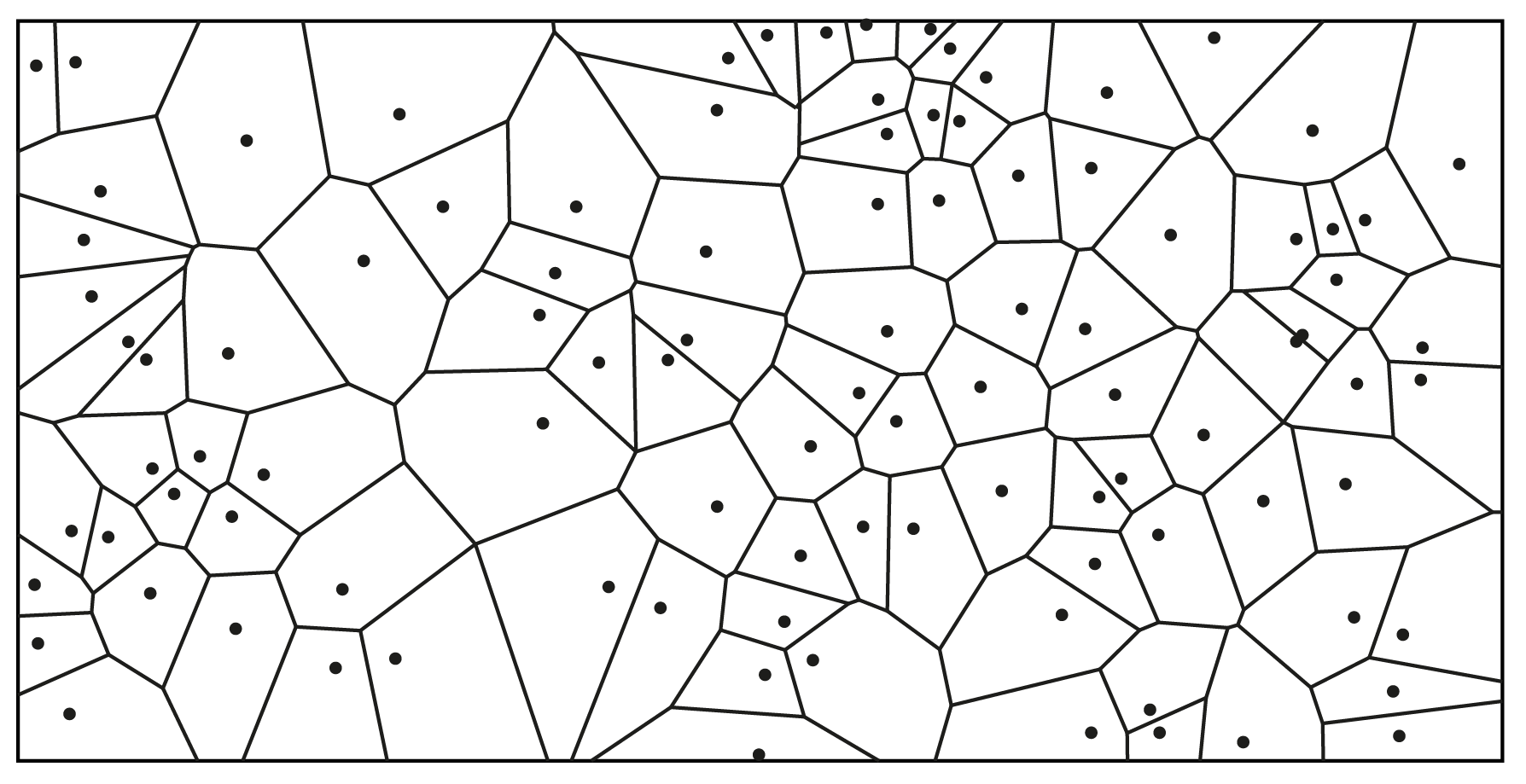
Opgave 1 Teken voor de vijf punten het bijbehorende Voronoidiagram met behulp van middelloodlijnen. Hint: als je de figuur $30^{\rm o}$ tegen de klok draait krijg je 'mooie' roosterpunten.

Maar hoe zit het met een Voronoidiagram als er landen in het spel zijn in plaats van punten? In januari 2023 kwam ik een illustratie in de Volkskrant tegen (figuur 2), bij de zoveelste ruzie tussen een aantal landen rondom de Zuid-Chinese Zee (onder andere China, Taiwan, Maleisië en de Filipijnen). Dat leek me een mooie aanleiding om te proberen Voronoidagrammen in de praktijk toe te passen.

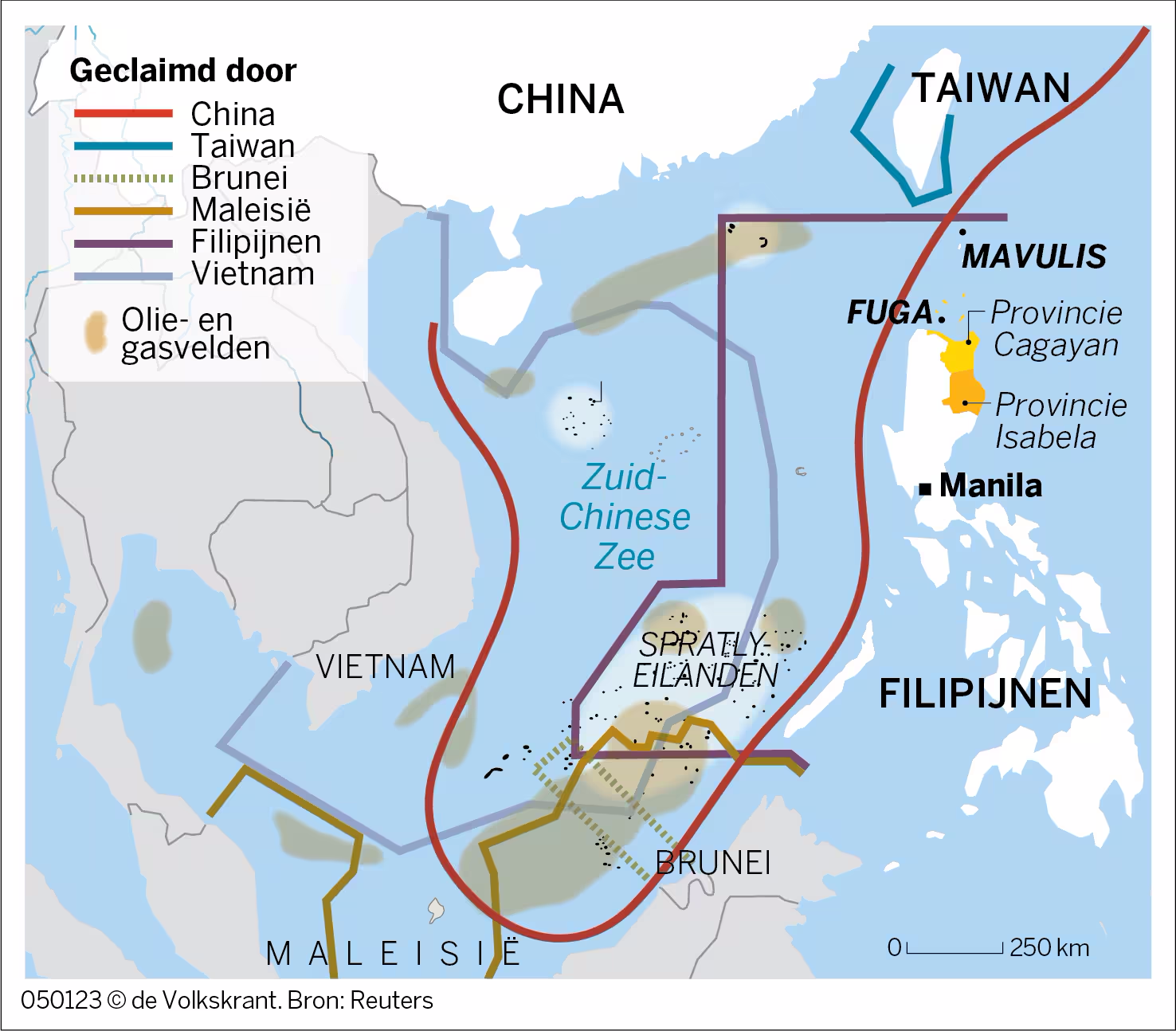
Het zou het eerlijkst zijn om van elk punt in de Zuid-Chinese Zee te bepalen wat de kortste afstand is tot een van de betrokken landen. Tot dát land behoort dan het punt in een Voronoiveelhoek. Alleen: omdat de landen geen punten zijn, worden de Voronoi-veelhoeken nu 'Voronoigebieden', niet noodzakelijkerwijs begrensd door alleen maar rechte lijnen.

Het idee is nu als volgt: ik geef je hieronder in figuur 3 drie gestileerde landen $A$, $B$ en $C$, beter gezegd gestileerde 'eilanden'. Daarmee moet jij de Voronoigebieden berekenen. Dan is bijvoorbeeld ook het 'equidistante punt' van deze drie (ei)landen exact bepaald: het punt dat even ver van alle drie de eilanden ligt.

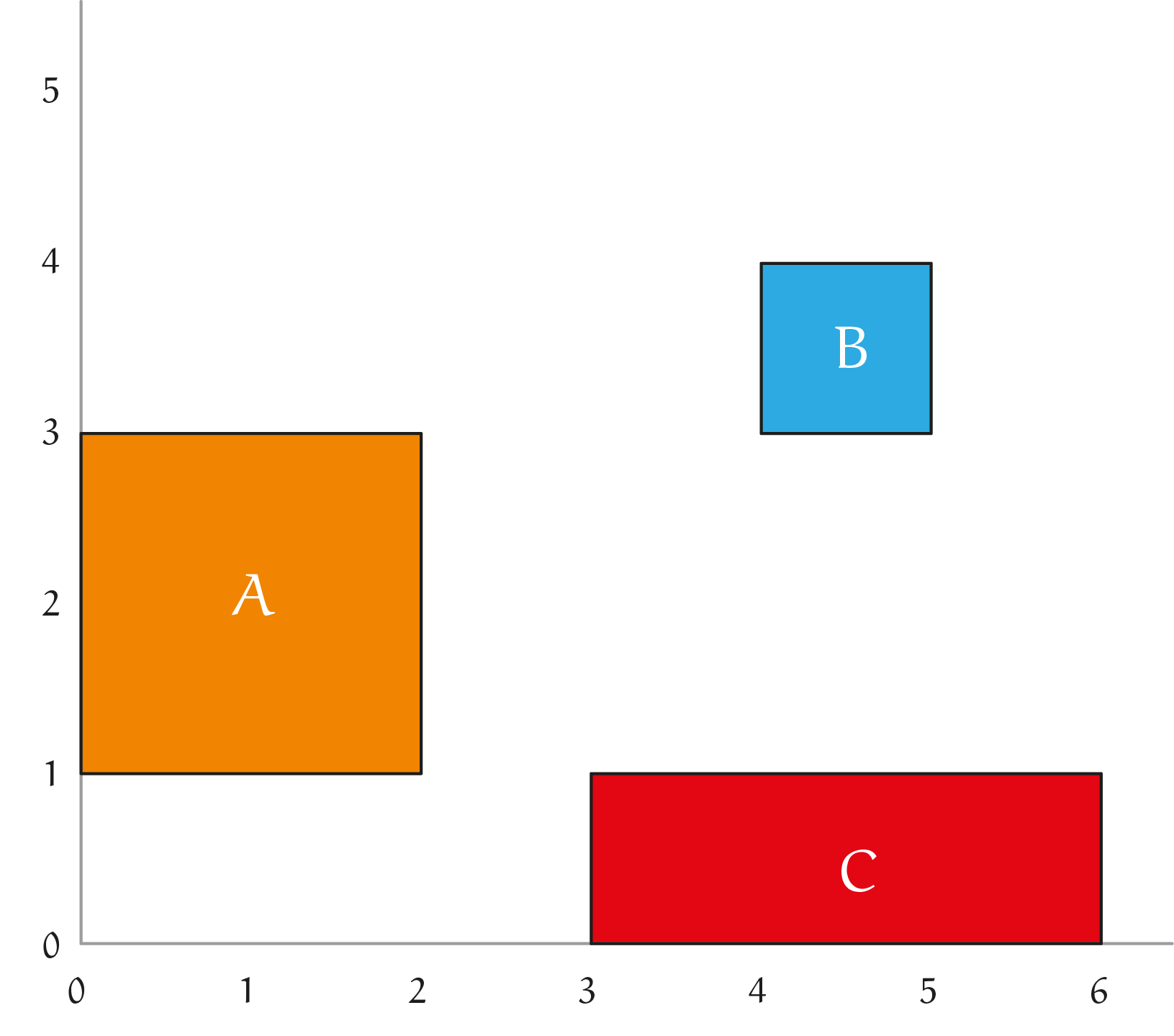
Hoe loopt bijvoorbeeld de 'Voronoikromme' tussen $A$ en $C$? Drie punten daarvan zijn direct duidelijk: $(2\tfrac{1}{2}, 1), (3, 2)$ en $(4, 3)$. Maar deze drie punten liggen niet op een rechte lijn, zoals bij het Voronoidiagram.

Opgave 2 Bepaal de exacte Voronoigebieden van $A$, $B$ en $C$. Opgave 3 Geef de coördinaten van het equidistante punt van de drie eilanden.

Hieronder nog wat hulp bij het oplossen van de opgaven 2 en 3.

Voor een punt $P = (x, y)$, op de Voronoikromme van $A$ en $C$, tussen de eerste twee gegeven punten, dus voor $2\tfrac{1}{2} \le x \le 3$, moet gelden dat de afstand tussen $A$ en $P$ gelijk is aan die tussen $C$ en $P$. Het dichtsbijzijnde punt in $C$ is $(3,1)$ en de kortste afstand tot $A$ is $x - 2$, dus moet gelden

$x - 2 = \sqrt{(x - 3)^2 + (y - 1)^2}$.

Links en rechts kwadrateren en vereenvoudigen levert

$x = \tfrac{1}{2}y^2 - y + 3$

of, met $y$ als functie van $x$ geschreven:

$y = 1 + \sqrt{2x - 5}$.

Tussen de punten $(2\tfrac{1}{2}, 1)$ en $(3, 2)$ heeft de Voronoikromme van $A$ en $C$ dus een parabolisch verloop!

Tussen de punten $(3, 2)$ en $(4, 3)$ is de Voronoikromme van $A$ en $C$ rechtlijnig. Hoe gaat dit verder?

Verder lezen Deze drie opgaven zijn onlangs gepubliceerd in het boek Denkstof. De oplossingen van de opgaven vind je hieronder bij [Bekijk oplossing]

Bekijk oplossing