
Worteltrekken in het graan
In het juninummer hebben we gezien hoe in Friesland, in Bildtse graanakkers, kunstwerken werden gemaakt, geïnspireerd door het werk van Escher. Deze keer bekijken we de wiskunde achter één van die kunstwerken: Conform schaakbord.
In het juninummer werd het kunstwerk, Conform schaakbord, als volgt gemaakt. Begin met een schaakbord, snij het in als in figuur 1 en vouw het zó dat het beeld ontstaat uit figuur 2.
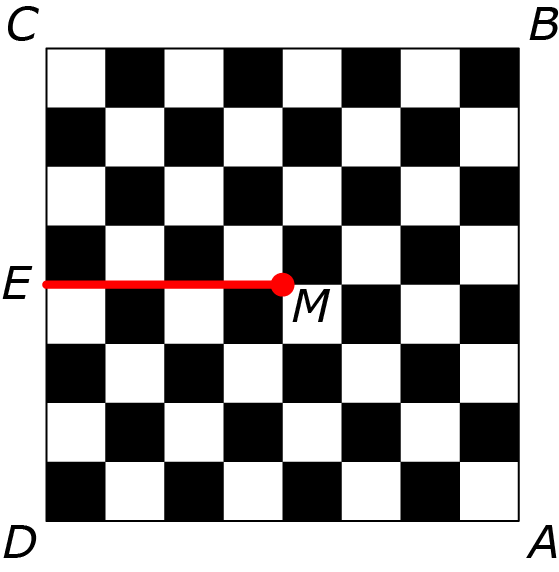
Figuur 1
|
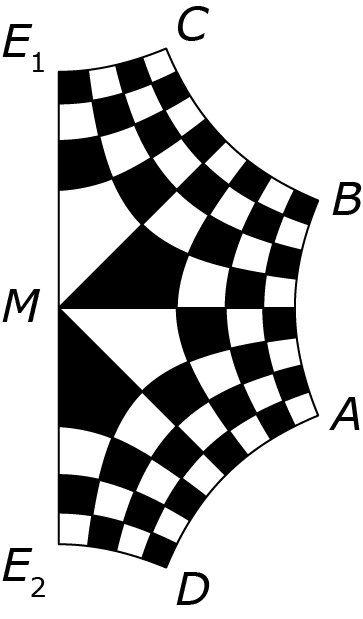
Figuur 2
|
We hebben de zaak hier ten opzichte van het juninummer een kwartslag gedraaid. Straks wordt duidelijk waarom.
Er werd niet uitgelegd hoe dat uitvouwen in zijn werk zou moeten gaan. In ieder geval niet door de hoeken die de lijnen door $M$ maken te halveren, zoals in een waaier. Dat zou figuur 3 geven.

Figuur 3
Hoe dan wel?
Vervormd schaakbord
In wiskundige termen is de vervorming van het schaakbord als volgt te beschrijven. Daartoe leggen we het schaakbord in een normaal $(x, y)$-assenstelsel zó dat het middelpunt $M$ samenvalt met de oorsprong $O.$ Als eenheid wordt de afmeting van een veld van het schaakbord gekozen, zodat alle hoekpunten samenvallen met roosterpunten van het assenstelsel. De vier uiterste hoekpunten van het bord hebben dan achtereenvolgens de coördinaten $(4, 4), (−4, 4), (−4, −4)$ en $(4, −4).$
In plaats van een punt vast te leggen met zijn $(x, y)$-coördinaten, kan dat ook met poolcoördinaten $(r, \vartheta).$
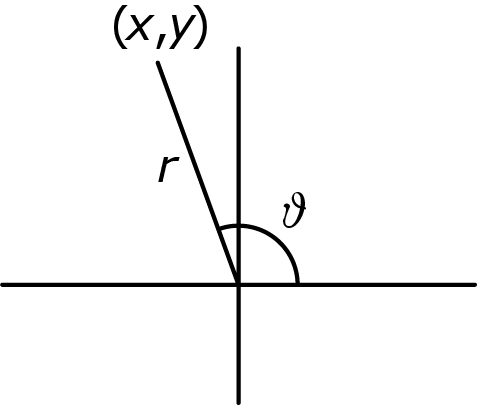
Figuur 4
Daarbij is $r$ de afstand van de oorsprong tot een punt, en $\vartheta$ de hoek tussen de plaatsvector van het punt en de positieve $x$-as. De hoek $\vartheta$ wordt uitgedrukt in radialen en loopt van $-\pi$ tot $\pi;$ positief boven de $x$-as, negatief onder de $x$-as.
De vier aangegeven uiterste hoekpunten van het bord hebben dan achtereenvolgens de coördinaten $(4\sqrt{2},\frac{\pi}{4})$, $(4\sqrt{2},\frac{3\pi}{4})$, $(4\sqrt{2},-\frac{3\pi}{4})$ en $(4\sqrt{2},-\frac{\pi}{4})$.
Ons derde plaatje, de waaier, ontstaat uit ons eerste plaatje door de volgende transformatie uit te voeren:
| $(r,\vartheta) \mapsto (r,\frac{1}{2}\vartheta)$ |
|
Dat is dus niet conform, want conform betekent dat na de transformatie alle hoeken tussen lijnen gelijk zijn gebleven.
Wat wel conform is is de volgende transformatie:
| $(r,\vartheta) \mapsto (\sqrt{r},\frac{1}{2}\vartheta)$ |
|
dus de hoek halveren èn de wortel uit de afstand tot $M$ trekken.
De vier hoekpunten worden dan overgevoerd in $(2\sqrt{\sqrt{2}},\frac{\pi}{8})$, $(2\sqrt{\sqrt{2}},\frac{3\pi}{8})$, $(2\sqrt{\sqrt{2}},-\frac{3\pi}{8})$ en $(2\sqrt{\sqrt{2}},-\frac{\pi}{8})$. Het resultaat hiervan is dus figuur 2.
De tweede helft van het patroon in het graan krijgen we door het resultaat een halve slag te draaien, in feite dus door deze transformatie toe te passen:
| $(r,\vartheta) \mapsto (\sqrt r,\frac12\vartheta+\pi).$ |
|
Over de transformatie
We zullen straks zien hoe je de transformatie ook in termen van gewone coördinaten kunt uitdrukken (dat ziet er wel wat ingewikkelder uit) maar een paar dingen kun je wel al opmerken. Punten op de eenheidscirkel, die met $r = 1$ dus, hebben hun beeldpunt op de eenheidscirkel, want $\sqrt{1}=1.$ Punten op de positieve $x$-as, die met $\vartheta = 0,$ hebben hun beeldpunt op de positieve $x$-as, want $0/2 = 0.$ Omdat $r<\sqrt{r}$ als $r < 1$ worden punten binnen de eenheidscirkel verder van de oorsprong afgebeeld; dat zie je aan de grote blokken binnen de eenheidscirkel. Buiten de eenheidscirkel, als $r > 1,$ hebben we $\sqrt{r}<r$ en dat veroorzaakt de krimp van de blokjes die verder weg liggen van $M.$
Rekenen
Het rekenen met poolcoördinaten lijkt lastig omdat we van niet veel punten makkelijk de bijbehorende hoek kunnen bepalen.
Hoe zou je bijvoorbeeld het beeldpunt van het punt met gewone coördinaten $(3, -4)$ berekenen? Er geldt $r=\sqrt{3^2+4^2}=5$, dat is makkelijk. Maar de hoek?
Die hoek hebben we eigenlijk niet nodig. Om dit te zien drukken we $x$ en $y$ uit in $r$ en $\vartheta:$
| $x=r\cos(\vartheta)\text{ en }y=r\sin(\vartheta)$ |
|
Zie figuur 5.
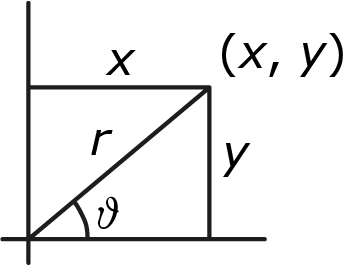
Figuur 5
Het beeldpunt onder de transformatie noemen we $(u, v).$ Dus
| $u=\sqrt r\cos\left(\frac{\vartheta}{2}\right)\text{ en }v=\sqrt r\left(\sin\frac{\vartheta}{2}\right).$ |
|
We hebben dus genoeg aan de cosinussen en de sinussen van de hoeken. Voor ons punt $(3, -4)$ hebben we $\cos(\vartheta) =\frac{3}{5}$ en $\sin(\vartheta) =-\frac{4}{5}.$
We kunnen gonioformules gebruiken om $u$ en $v$ uit te drukken in $x$ en $y.$ We gebruiken hierbij
| $\cos(2t) = \cos^2(t) - \sin^2(t)$ |
(1) |
en
| $\sin(2t) = 2\sin(t)\cdot\cos(t)$ |
(2) |
In formule (1) nemen we $t=\frac{1}{2}\vartheta$ en vermenigvuldigen links en rechts met $r=\sqrt{r^2}$, dan staat er
| $x = u^2 - v^2$ |
($*$) |
In formule (2) doen we hetzelfde, dan komt er
| $y = 2uv$ |
($**$) |
Ga dit zorgvuldig na.
We kunnen nog een vergelijking maken door ons recept ook toe te passen op
| $1 = \cos^2(t) + \sin^2(t)$ |
|
dan komt er namelijk
| $\sqrt{x^2+y^2} = u^2 + v^2$ |
($***$) |
Voor het punt $(3, -4)$ leidt dit dus achtereenvolgens tot $u^2-v^2=3, 2uv=-4$ en $u^2+v^2=5.$
Als je vergelijkingen ($*$) en ($***$)samen neemt kun je ze oplossen naar $u^2$ en $v^2:$
| $u^2=\frac{1}{2}(\sqrt{x^2+y^2}+x)$ |
|
en
| $v^2=\frac{1}{2}(\sqrt{x^2+y^2}-x).$ |
|
In ons voorbeeld: $u^2 = \frac{1}{2}(5+3)=4,$ en $v^2=\frac{1}{2}(5-3)=1.$ Dat geeft vier mogelijke combinaties: $u = \pm 2$ en $v = \pm 1.$ Uit het plaatje wordt duidelijk dat we het punt $(2, -1)$ moeten hebben:
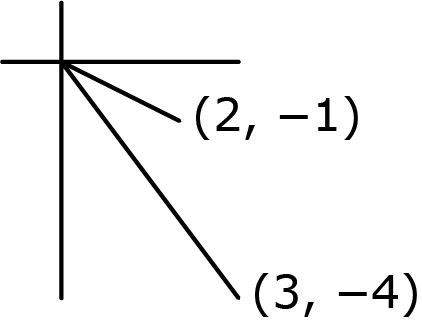
Figuur 6
Hadden we dat ook aan de formules kunnen zien? Ja: omdat $2uv = -4$ weten we dat $u$ en $v$ tegengesteld teken moeten hebben, dus $(2, -1)$ of $(-2, 1).$ En omdat $(3, -4)$ onder de $x$-as ligt moeten we de mogelijkheid onder de $x$-as hebben, $(2, -1)$ dus.
Hyperbolen
Formules ($*$) en ($**$) helpen ook bij het tekenen van het patroon. Het beeld van de verticale lijn $x = 3$ rekenen we snel uit: er moet gelden dat $u^2-v^2=3.$ Dat is de vergelijking van een hyperbool, hiervan moeten we de rechtertak hebben.
Het beeld van de horizontale lijn $y = -4$ heeft als vergelijking $2uv=-4$ en dat geeft ook een hyperbool, nu moeten we de tak in het vierde kwadrant hebben.
De keuze voor de tak wordt in beide gevallen bepaald door de eis dat $u > 0.$
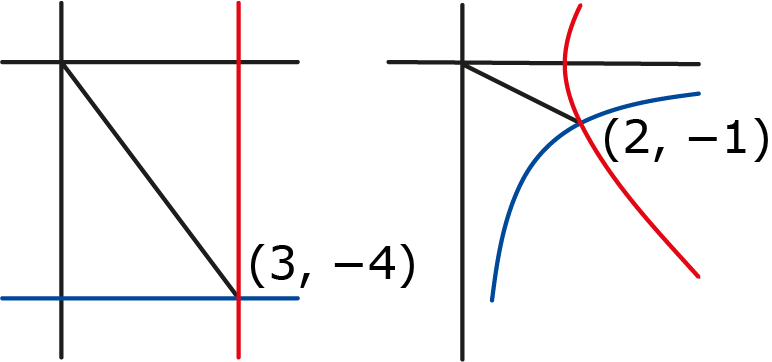
Figuur 7
En als je goed in figuur 7 kijkt zie je dat de rode en blauwe hyperbool elkaar loodrecht snijden. Dit kun je natuurlijk ook nagaan:
Opgave 1
Bereken de richtingscoëfficiënten van de raaklijnen aan de hyperbolen in $(2, -1)$ en ga na dat hun product gelijk is aan $-1.$
Opgave 2
Neem twee getallen $a$ en $b$ ongelijk aan $0.$ Laat zien dat de hyperbolen met vergelijkingen $u^2-v^2=a$ en $2uv = b$ elkaar loodrecht snijden.
Waarom worteltrekken?
Waarom hebben we het over worteltrekken in het graan?
Wie bij Wiskunde D kennis heeft gemaakt met complexe getallen weet dit al: de relatie tussen de punten $(x, y)$ en $(u, v)$ kun je door complexe vermenigvuldiging weergeven: $x + yi = (u + v{\rm i})^2.$ Je zou dus $u + v{\rm i}$ een vierkantswortel van $x + y{\rm i}$ kunnen noemen.
Voor wie dit nog niet gezien heeft: je kunt de punten in het platte vlak met elkaar vermenigvuldigen. De definitie is
| $(a,b)\cdot(c,d)=(ac-bd,ad+bc)$ |
|
Je kunt dit ook met behulp van lengte en hoek doen, dit werd in 1797 door de Noorse wiskundige Caspar Wessel gedaan. Hij nam van twee punten de poolcoördinaten en hoek, $(r, \vartheta)$ en $(s, \varphi),$ en definieerde het product als het punt met poolcoördinaten
| $(rs,\vartheta+\varphi).$ |
|
Dat dit werkt kunnen we met behulp van gonioformules narekenen.
Bepaal de gewone coördinaten van het product:
| $(rs\cos(\vartheta+\varphi,rs\sin(\vartheta+\varphi)).$ |
|
Werk beide coördinaten om:
| $rs\cos(\vartheta+\varphi)=r\cos(\vartheta)\cdot s\cos(\varphi)-r\sin(\vartheta)\cdot s\sin(\varphi)$ |
|
en
| $rs\sin(\vartheta+\varphi)=r\cos(\vartheta)\cdot s\sin\varphi+r\sin(\vartheta)\cdot s\cos(\varphi)$ |
|
dat komt precies overeen met de eerste definitie van het product van de punten $(r\cos(\vartheta),r\sin(\vartheta))$ en $(s\cos(\varphi),s\sin(\varphi))$.
Als we de methode van Wessel gebruiken kunnen we de transformatie ‘kwadrateren’ dus als volgt noteren:
| $(r,\vartheta) \mapsto (r^2,2\vartheta).$ |
|
De conforme transformatie van het schaakbord is daar precies de inverse van
| $(r,\vartheta) \mapsto (\sqrt r,\frac{1}{2}\vartheta).$ |
|
Vandaar dat dit artikel Worteltrekken in het Graan heet.
Door middel van deze twee manieren om tegen het vermenigvuldigen van punten in het vlak getallen aan te kijken kun je een heleboel meetkunde op algebraïsche wijze aanpakken, en omgekeerd.
Kijk maar eens op de website van Math4All voor materiaal over Complexe Getallen.
Caspar Wessel: Om directionens analytiske betegning, et forsog, anvendt fornemmelig til plane og sphaeriske polygoners oplosning. Zie https://archive.org/stream/nyesamlingafdetk5179kong#page/468/mode/2up
