De stelling van Ptolemaeus is een veralgemenisering van de stelling van Pythagoras die we denk ik allemaal wel kennen. Het bewijs voor de stelling van Ptolemaeus is ook een stuk ingewikkelder dan het bewijs voor de stelling van Pythagoras, maar dat is te verwachten als een stelling veralgemeniseerd wordt. Toch kwam ik een YouTube filmpje tegen dat die stelling op zeer elegante wijze bewijst, A Miraculous Proof (Ptolemy’s Theorem) van Zvezdelina Stankova. Het geeft niet alleen een mooi bewijs, maar laat ook zien hoe door geometrische inversie rechte lijnen veranderen in cirkels, iets dat we ook tegenkomen bij functieanalyse in het complexe vlak, maar daarover een andere keer meer. Overigens laat het filmpje zien
dat rechte lijnen door de oorsprong rechte lijnen blijven, maar een rechte lijn is in feite niets anders dan een cirkelsegment van een cirkel met oneindig grote straal. Hoe dichter een rechte lijn bij de oorsprong komt, hoe groter de straal van de cirkel wordt na inversie, met als resultaat dat die straal oneindig wordt als de lijn door de oorsprong gaat. 

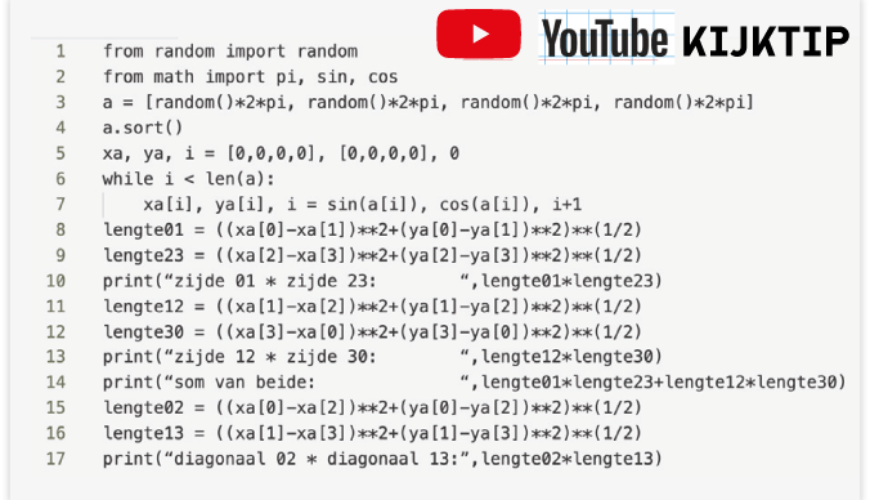
Voor wie ook proefondervindelijk wil zien dat de stelling van Ptolemaeus correct is, heb ik ook een Pythonprogramma geschreven, waar een willekeurige vierhoek met punten op de eenheidscirkel wordt gegenereerd. Onder de knop [Bekijk oplossing], hieronder, staat het uitgeschreven. Bekijk zelf maar regel voor regel hoe het programma werkt, raadpleeg daarvoor eventueel een Python tutorial op internet als dat nodig blijkt. 

Nu zal de vraag misschien zijn, "wat kun je met die stelling van Ptolemaeus?". Twee leuke voorbeeldjes worden je gegeven in het filmpje Pentagons and the Golden Ratio eveneens van Zvezdelina Stankova.

• A Miraculous Proof (Prolemy's Theorem): www.youtube.com/watch?v=bJOuzqu3MUQ
• Voorbeeld: Pentagons and the Golden Ratio: www.youtube.com/watch?v=o3QBgkQi_HA
• Wil je een toegift? www.youtube.com/watch?v=p7oGGSwUFwM

Veel kijk- en leerplezier!

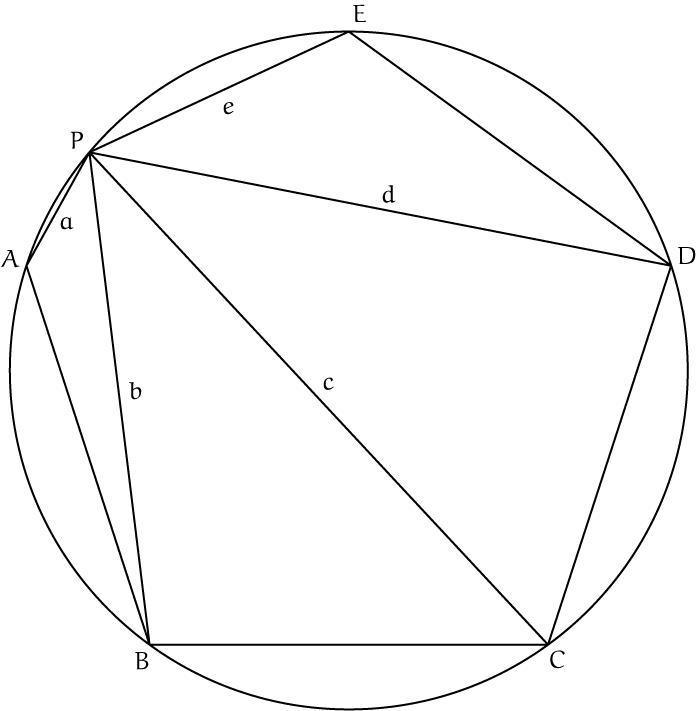
Opgave Laat $ABCDE$ een gelijkzijdige vijfhoek zijn, en $P$ een willikeurig punt tussen $A$ en $E$ op de cirkel die de vijfhoek omschrijft. Toon aan dat $a+c+e = b+d$.

 

Bekijk oplossing