De zelfbeschrijvende vergelijking van Tupper, of eigenlijk de ongelijkheid van Tupper, luidt als volgt:

$$\frac{1}{2} < \left\lfloor{\rm mod}\left(\left\lfloor\frac{y}{17}\right\rfloor\cdot 2^{-17\lfloor x\rfloor-{\rm mod}(\lfloor y\rfloor,17)},2\right)\right\rfloor.$$

Geen zorgen als dit er eng uitziet vanwege ${\rm mod}$ en de haakjes $\lfloor \ \ \rfloor$, alles wat je moet weten wordt zo uitgelegd. Waarom heet dit de zelfbeschrijvende formule van Tupper? Wel, beschouw het volgende $543$-cijferige getal:

$K$		$=$		$960$		$939$		$379$		$918$		$958$		$884$		$971$		$672$		$962$		$127$		$852$		$754$		$715$		$004$
$339$		$660$		$129$		$306$		$651$		$505$		$519$		$271$		$702$		$802$		$395$		$266$		$424$		$689$		$642$		$842$
$174$		$350$		$718$		$121$		$267$		$153$		$782$		$770$		$623$		$355$		$993$		$237$		$280$		$874$		$144$		$307$
$891$		$325$		$963$		$941$		$337$		$723$		$487$		$857$		$735$		$749$		$823$		$926$		$629$		$715$		$517$		$173$
$716$		$995$		$165$		$232$		$890$		$538$		$221$		$612$		$403$		$238$		$855$		$866$		$184$		$013$		$235$		$585$
$136$		$048$		$828$		$693$		$337$		$902$		$491$		$454$		$229$		$288$		$667$		$081$		$096$		$184$		$496$		$091$
$705$		$183$		$454$		$067$		$827$		$731$		$551$		$705$		$405$		$381$		$627$		$380$		$967$		$602$		$565$		$625$
$016$		$981$		$482$		$083$		$418$		$783$		$163$		$849$		$115$		$590$		$225$		$610$		$003$		$652$		$351$		$370$
$343$		$874$		$461$		$848$		$378$		$737$		$238$		$198$		$224$		$849$		$863$		$465$		$033$		$159$		$410$		$054$
$974$		$700$		$593$		$138$		$339$		$226$		$497$		$249$		$461$		$751$		$545$		$728$		$366$		$702$		$369$		$745$
$461$		$014$		$655$		$997$		$933$		$798$		$537$		$483$		$143$		$786$		$841$		$806$		$593$		$422$		$227$		$898$
$388$		$722$		$980$		$000$		$748$		$404$		$719$

Als nu de punten $(x, y)$ worden geplot die voldoen aan de ongelijkheid van Tupper in het frame $0 \le x < 106$ en $K \le y < K + 17$, dan krijgen we de grafiek in figuur 1. Merk op dat de richting van de assen is omgedraaid, daar straks meer over. 

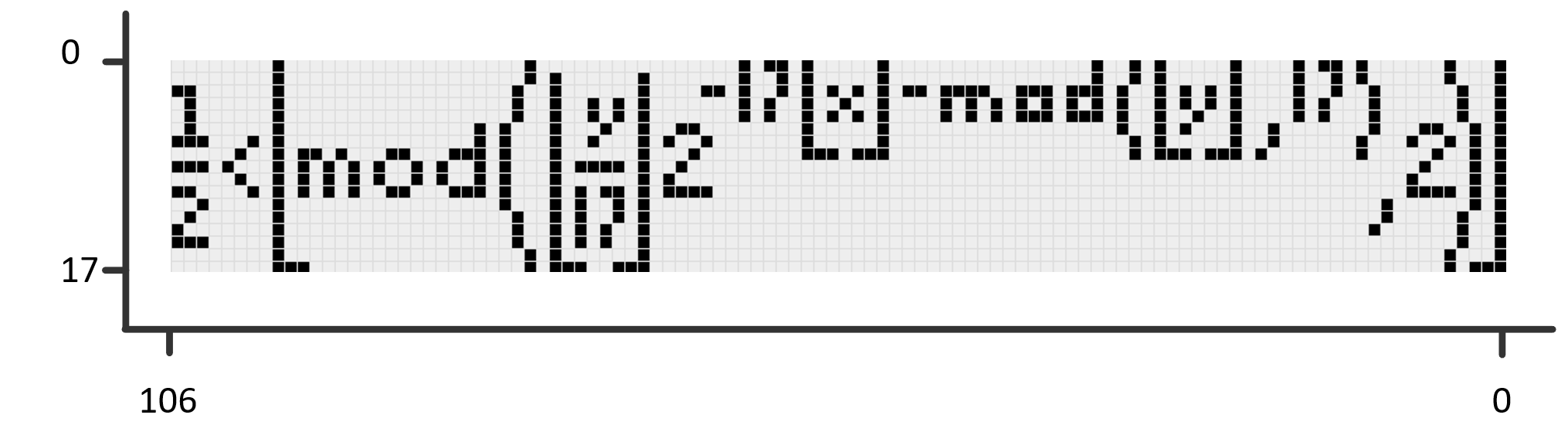
En inderdaad, we zien zowaar de ongelijkheid van Tupper geplot als punten die voldoen aan de ongelijkheid van Tupper in een specifiek $x$ en $y$ frame. Hoe krankzinnig is dat! En een dergelijke plot kunnen we vinden voor elk mogelijk plaatje van $106$ bij $17$ pixels. We zullen in dit artikel leren hoe we een dergelijke plot vinden, en dat zal voornamelijk neerkomen op het juiste getal $K$ vinden. Eerst gaan we echter zoals beloofd kijken naar wat begrippen die nodig zijn om deze vergelijking te begrijpen en die nodig zullen zijn bij de zoektocht naar de $K$'s.

Begrippen

Modulorekenen. Laten we allereerst kijken naar de betekenis van ${\rm mod}$. Eigenlijk gebruik je dit elke dag al wanneer je naar een digitale klok kijkt. Als je ziet dat het 17:00 uur is, dan zou je dat uitspreken als 'vijf uur' en zo zou je 21:00 uitspreken als 'negen uur'. Wat je hier dus doet is $17$ en $21$ verminderen met $12$ of ook wel  delen door twaalf met rest en dan de rest uitspreken. Voornamelijk dit laatste is waar je aan moet denken bij modulorekenen. Modulorekenen is eigenlijk niets anders dan delen met rest. Deel je $17$ door $3$ met rest, dan zul je vinden dat de rest gelijk is aan $2$, er geldt immers $17 = 5 \cdot 3 + 2$. Bij modulo rekenen noteren we dit als $17 {\rm\ mod\ } 3 = 2$ of als ${\rm mod}(17, 3) = 2$. Nog een voorbeeld: $89 {\rm\ mod\ } 7 = 5$ want $89 = 12 \cdot 7 + 5$ dus delen van $89$ door $7$ geeft rest $5$.

Afronden. Naast modulo rekenen hebben we ook een stukje notatie nodig dat wellicht niet bekend is. Als $x$ een reëel getal is, dan noteren we $\lfloor x\rfloor$ voor het grootste gehele getal dat kleiner dan of gelijk is aan $x$. Zo hebben we $\lfloor\pi\rfloor = 3$, $\lfloor-3{,}75\rfloor = -4$ en $\lfloor\frac{4}{3}\rfloor=1$, om een aantal voorbeelden te geven. Dit is dus eigenlijk afronden naar beneden op gehele getallen.

Binaire getallen. Als laatste hebben we nog begrip van binaire getallen nodig. Deze zijn niet nodig bij het begrijpen van de vergelijking, maar ze zullen later belangrijk zijn bij het vinden van een getal $K$ als we zelf afbeeldingen gaan maken. Binaire getallen zijn getallen uitgedrukt met nullen en enen, in het tweetallig stelsel dus. In het tientallig stelsel weten we dat de rij cijfers $678$ het getal $6 \cdot 10^2 + 7 \cdot 10^1 + 8 \cdot 10^0$ uitdrukt. Hebben we nu een binair getal $1101$, dan kunnen we deze begrijpen als $1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0$. De tientallige of ook wel decimale representatie van $1101$ vinden we dan simpelweg door $1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0$ uit te rekenen, we krijgen $13$.

De formule

Nu zijn we klaar om Tuppers ongelijkheid wat beter te begrijpen. We kijken dus naar punten $(x, y)$ in het $xy$-vlak waarbij we ons beperken tot de $106$ bij $17$ rechthoek binnen $0 \le x < 106$ en $K \le y < K + 17$, voor een zekere $K$. Zoals gezegd worden alle punten $(x, y)$ geplot die voldoen aan Tuppers ongelijkheid.
Laten wij nu voor het gemak eens kijken naar het geval dat $K = 0$. Een punt dat nu in het $106$ bij $17$ vlak ligt met $0 \le x < 106$ en $0 \le y < 0 + 17$ ligt is  bijvoorbeeld $(1, 1)$. Als we willen controleren of dit punt wordt geplot moeten we kijken of de uitdrukking in de rechterkant van Tuppers ongelijkheid bij invullen van dit punt groter is dan $\frac{1}{2}$. Invullen geeft

$$\begin{align*} \left\lfloor{\rm mod}\left(\left\lfloor\frac{1}{17}\right\rfloor\cdot 2^{-17\lfloor 1\rfloor-{\rm mod}(\lfloor 1\rfloor,17)},2\right)\right\rfloor &= \left\lfloor{\rm mod}\left(0\cdot 2^{-17\cdot 1-{\rm mod}(1,17)},2\right)\right\rfloor\\ &= \left\lfloor{\rm mod}\left(0,2\right)\right\rfloor\\ &= \left\lfloor 0\right\rfloor = 0. \end{align*}$$

Er geldt dat $\frac{1}{2} > 0$ dus het punt $(1, 1)$ voldoet niet aan de ongelijkheid van Tupper en zal dus ook niet worden geplot. Sterker nog, omdat voor alle $y$ in de huidige rechthoek geldt $0 ≤ y < 17$, zullen we altijd hebben dat $\frac{y}{17} < 1$ en dus $\left\lfloor\frac{y}{17}\right\rfloor=0$. Geen enkel punt in deze rechthoek zal dus worden geplot, dit is dus een leeg plaatje! Echter als we grotere waarden voor $K$ kiezen, dan zal niet meer gelden $\frac{y}{17}<1$. We moeten voor $K$ namelijk een $17$-voud kiezen, precies de hoogte van de rechthoeken. Zo is er geen overlap tussen de rechthoeken en zal dus per $17$ stappen op de $y$-as een nieuwe rechthoek voorkomen. Welke $K$ we ook hebben, het is sowieso een goed idee om per rechthoek de computer een plot te laten maken, want anders moeten we de ongelijkheid $106 \times 17 = 1082$ keer controleren, geen pretje!

De zoektoCht naar k

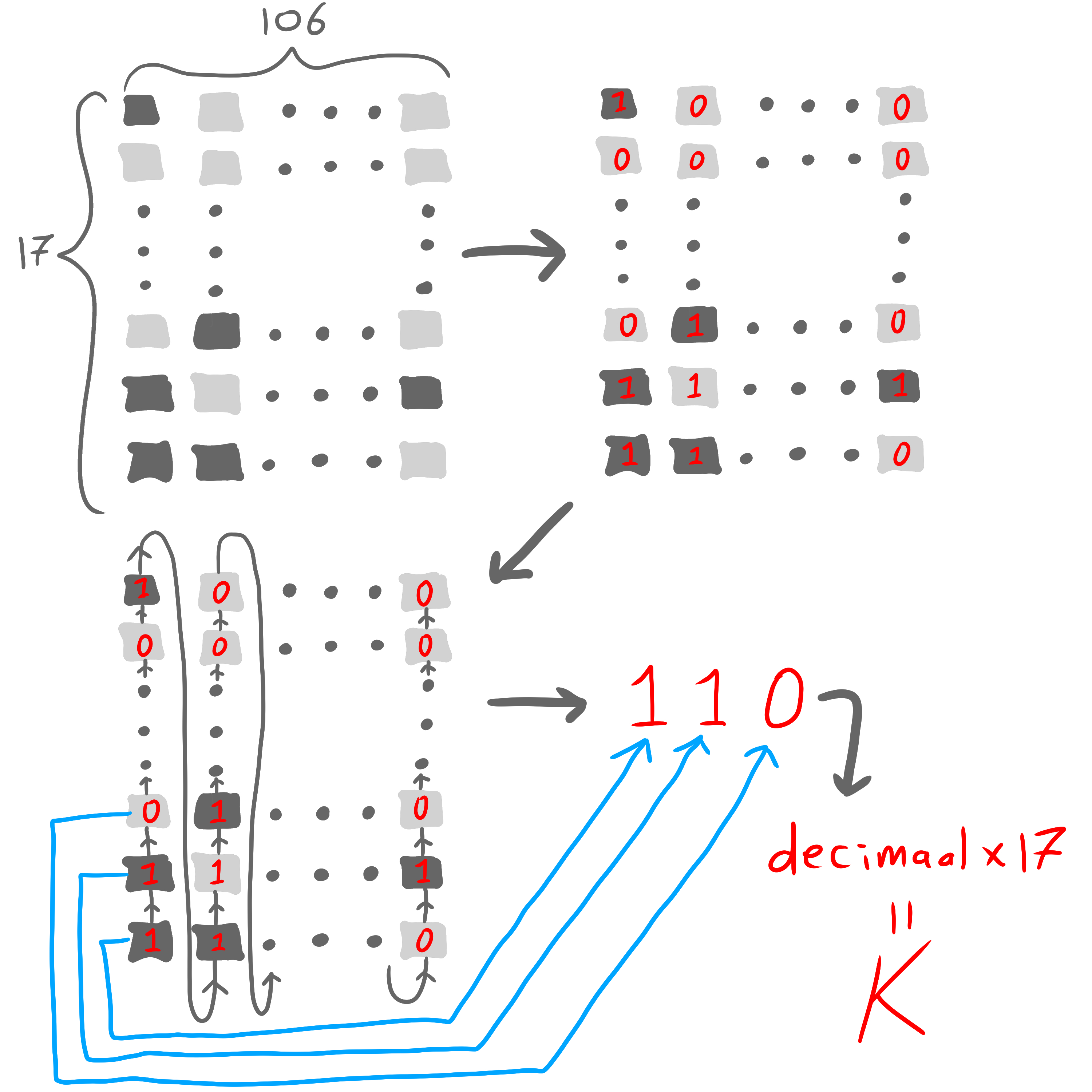
Laten we nu eens kijken hoe we die getallen $K$ kunnen vinden. Zoals gezegd kunnen we bij elk plaatje van $106$ bij $17$ pixels een getal $K$ vinden zodat het plaatje wordt geplot voor punten $(x, y)$ met $0 \le x < 106$ en $K \le y < K + 17$ die voldoen aan Tuppers ongelijkheid. Het volgende stappenplan legt uit hoe we $K$ bij een  plaatje kunnen vinden.

		Stappenplan Teken een plaatje van $106$ bij $17$ pixels. Gebruik enkel witte of zwarte pixels. Vul nu voor alle witte pixels een $0$ in en voor alle zwarte pixels een $1$. Nu zetten we het plaatje om in een binair getal. Begin links onderin je plaatje en lees van onder naar boven in de kolom de getallen  af die je ziet, $0$ of $1$. Als je klaar bent met de kolom, ga dan naar de eerstvolgende kolom aan de rechterkant en begin onderaan weer met lezen. Zo ga je door met lezen tot je rechts bovenaan in je plaatje eindigt.  Nu heb je een heel lang binair getal (deze heeft lengte $1082$, voor elke pixel in de rechthoek een $0$ of $1$). Zet dit binaire getal om in een decimaal getal (tientallig). Vermenigvuldig vervolgens het resultaat met $17$. En voilà, daar heb je je getal $K$ bij het  [laatje, zie ook de visualisatie van dit stappenplan in figuur 2.

Wat wel belangrijk is: het getal $K$ dat je zo krijgt zal een plaatje opleveren waarbij de $x$-as van rechts naar links loopt en de $y$-as van boven naar beneden, zoals we al zagen in figuur 1. De richtingen van de assen zijn dus omgekeerd. Dit komt door de manier waarop Tupper een rooster van pixels opslaat, het is anders dan we zijn gewend in de wiskunde. Om echt het goede plaatje te krijgen moet je je plot nog dus nog horizontaal en verticaal spiegelen, maar voor nu zullen wij de assen gewoon omgekeerd weergeven.

Waarschijnlijk is het lastig om het bovenstaande stappenplan te volgen met enkel je rekenmachine en zelfs met je computer moet je weten wat je doet, je werkt immers
met gigantische getallen. Er zijn echter mensen die hier al mooie programma’s voor hebben geschreven, zoek op internet bijvoorbeeld eens naar Tupper’s Self-Referential Formula Playground. Bij het eerste resultaat vind je een website die het mogelijk maakt om alle stappen in het stappenplan met gemak uit te voeren! Maar ook andersom, stel dat je al een getal $K$ hebt, dan is het op deze website mogelijk om de plot te zien. Op deze website zijn de assen van de plot ook in omgekeerde richting, dus de $K$ die we met het bovenstaande stappenplan vinden zou hier een normaal plaatje opleveren, het spiegelen is al voor ons gedaan. Met deze website hebben we bijvoorbeeld met gemak het volgende getal kunnen vinden.

$K$		=		$015$		$683$		$295$		$494$		$229$		$487$		$001$		$347$		$799$		$175$		$458$		$384$		$351$		$263$
$336$		$152$		$877$		$634$		$416$		$628$		$098$		$182$		$395$		$917$		$073$		$583$		$944$		$206$		$829$		$561$
$004$		$038$		$741$		$872$		$964$		$334$		$337$		$617$		$343$		$106$		$365$		$249$		$763$		$782$		$544$		$012$
$358$		$998$		$562$		$128$		$648$		$728$		$417$		$984$		$544$		$668$		$088$		$298$		$261$		$021$		$286$		$087$
$547$		$836$		$725$		$919$		$084$		$534$		$235$		$473$		$223$		$960$		$126$		$102$		$809$		$479$		$938$		$377$
$925$		$271$		$709$		$993$		$975$		$087$		$803$		$806$		$484$		$549$		$588$		$618$		$062$		$663$		$663$		$064$
$421$		$315$		$354$		$739$		$964$		$801$		$095$		$328$		$493$		$207$		$787$		$302$		$133$		$770$		$977$		$359$
$399$		$247$		$579$		$959$		$317$		$683$		$041$		$891$		$387$		$120$		$757$		$425$		$458$		$878$		$018$		$484$
$947$		$621$		$711$		$534$		$026$		$050$		$265$		$313$		$255$		$595$		$586$		$030$		$254$		$091$		$397$		$298$
$055$		$242$		$906$		$836$		$344$		$198$		$693$		$289$		$468$		$900$		$663$		$057$		$039$		$950$		$506$		$703$
$327$		$663$		$363$		$742$		$755$		$039$		$179$		$791$		$581$		$789$		$786$		$265$		$551$		$372$		$288$

wat het Pythagoras-logo geeft (figuur 3): 

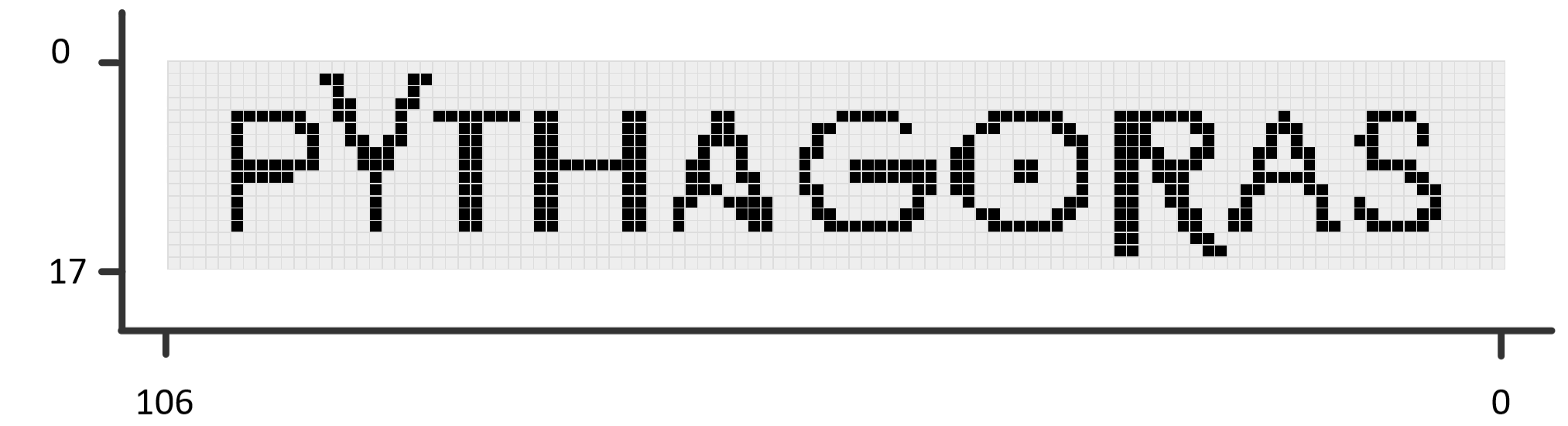
Dat is nog eens een manier om een lievelingsgetal te vinden, zet een mooi plaatje van $106$ bij $17$ pixels volgens het stappenplan om in een getal $K$. Maar je moet dan wel grondig de vraag naar jouw lievelingsgetal vermijden, anders sta je lang cijfers op te noemen!

 

Opgave 1 Welke boodschap hoort bij: $K$    =    $921$    $835$    $551$    $606$    $733$    $470$    $677$    $315$    $587$    $500$    $024$    $893$    $552$    $897$ $227$    $190$    $507$    $622$    $109$    $445$    $623$    $648$    $844$    $067$    $268$    $369$    $390$    $491$    $849$    $537$ $957$    $695$    $263$    $523$    $723$    $627$    $945$    $197$    $641$    $765$    $641$    $517$    $652$    $895$    $190$    $911$ $323$    $628$    $354$    $919$    $781$    $523$    $793$    $893$    $176$    $934$    $361$    $817$    $421$    $855$    $051$    $643$ $004$    $325$    $410$    $549$    $754$    $048$    $491$    $039$    $203$    $861$    $145$    $188$    $039$    $380$    $542$    $991$ $087$    $752$    $196$    $405$    $499$    $571$    $234$    $869$    $571$    $956$    $997$    $846$    $027$    $440$    $094$    $779$ $857$    $281$    $214$    $613$    $174$    $990$    $884$    $464$    $929$    $604$    $015$    $589$    $295$    $288$    $640$    $019$ $318$    $581$    $287$    $682$    $324$    $717$    $684$    $738$    $022$    $901$    $246$    $833$    $880$    $215$    $657$    $295$ $734$    $313$    $334$    $958$    $779$    $549$    $650$    $925$    $653$    $064$    $452$    $731$    $475$    $986$    $285$    $463$ $804$    $204$    $039$    $161$    $625$    $859$    $954$    $316$    $410$    $123$    $546$    $193$    $076$    $417$    $315$    $363$ $144$    $988$    $240$    $576$    $156$    $205$    $221$    $069$    $811$    $435$    $300$    $473$    $934$    $641$    $912$    $348$ $672$    ?