Opgave 1

sinusregel.

Opgave 2

cosinusregel.

Opgave 3

cosinusregel.

Opgave 4

tangensregel.

Opgave 5

$\alpha = 75^{\rm o}$ en $\beta = 47^{\rm o}$.

Opgave 6

$AB=3{,}5$.

Opgave 7

Tip: vermijd tussentijds afronden.

Opgave 8

Gegeven is driehoek $ABC$ met $a=BC=66$ en $c=AB=105$ en $\beta = \angle ABC=56\frac{50}{60}^{\rm o}$. Invullen in $\frac{c+a}{c-a}=\frac{\tan\left(\tfrac12(\gamma+\alpha)\right)}{\tan\left(\tfrac12(\gamma-\alpha)\right)}$ geeft $\frac{171}{39}=\frac{\tan\left(61\frac{3}{12}^{\rm o}\right)}{\tan\left(\tfrac12(\gamma-\alpha)\right)}$. $\tan\left(\tfrac12(\gamma+\alpha)\right)=1{,}8481\ldots$ en $\tan\left(\tfrac12(\gamma-\alpha)\right)=0{,}4215\ldots$ waardoor, afgerond op 2 decimalen, $\tfrac12(\gamma-\alpha)\approx22{,}86^{\rm o}$ zodat $\angle BAC\approx38{,}73^{\rm o}$ en $\angle BCA\approx 84{,}44^{\rm o}$.

Opgave 9

In gelijkbenige driehoek $BCD$ is $\angle BCD = \alpha + \beta = 180^{\rm o} - \gamma$ zodat $\angle BDC = \angle CBD = \tfrac12\gamma$.

Opgave 10

In gelijkbenige driehoek $ACO$ is $\angle ACO = \gamma$ zodat $\angle CAO = \angle COA = \tfrac12\left(180^{\rm o}-\gamma\right)=\tfrac12\alpha + \tfrac12\beta$.

Opgave 11

Omdat $\angle BOE = \angle AOC = \tfrac12\alpha+\tfrac12\beta$ en $\angle OBE = \angle CBD = \frac12\gamma$ en $\alpha + \beta + \gamma = 180^{\rm o}$ geldt $\angle BEO = 180^{\rm o}-\frac12\gamma-\tfrac12\alpha-\tfrac12\beta=90^{\rm o}$ en dus is driehoek $BEO$ rechthoekig.

Opgave 12

In rechthoekige driehoek $BEO$ is $\angle BOE=\frac12\alpha+\frac12\beta$. Vanuit hoekpunt $O$ gezien is zijde $BE$ de overstaande en zijde $EO$ de aanliggende. Daarom is $\tan\left(\frac12\alpha + \frac12\beta\right)=\frac{BE}{EO}$.

Opgave 13

In rechthoekige driehoek $ABE$ is $\angle BAE=\angle BAC-\angle CAO=\alpha-\left(\frac12\alpha+\frac12\beta\right)=\frac12\alpha-\frac12\beta$. Vanuit hoekpunt $A$ gezien is zijde $BE$ de overstaande en zijde $AE$ de aanliggende. Daarom is $\tan\left(\frac12\alpha-\frac12\beta\right) = \frac{BE}{AE}.$

Opgave 14

Gebruikmakend van de sinusregel $\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}=f$ kun je via $a=f\cdot\sin(\alpha)$ en $b=f\cdot\sin(\beta)$ de uitdrukking $\frac{a+b}{a-b}$ herleiden tot

$$\frac{f\cdot\sin(\alpha)+f\cdot\sin(\beta)}{f\cdot\sin(\alpha)-f\cdot\sin(\beta)}=\frac{\sin(\alpha)+\sin(\beta)}{\sin(\alpha)-\sin(\beta)}.$$

Opgave 15

Gebruikmakend van de som- en verschilformule kom je uit op de uitdrukking

$$\frac{2\sin\left(\frac12(\alpha+\beta)\right)\cos\left(\frac12(\alpha-\beta)\right)}{2\sin\left(\frac12(\alpha-\beta)\right)\cos\left(\frac12(\alpha+\beta)\right)}$$

dus 

$$\frac{\sin\left(\frac12(\alpha+\beta)\right)}{\cos\left(\frac12(\alpha+\beta)\right)}\cdot\frac{\sin\left(\frac12(\alpha-\beta)\right)}{\cos\left(\frac12(\alpha-\beta)\right)}$$

en dan tot

$$\tan\left(\frac12(\alpha+\beta)\right)\cdot\frac{1}{\tan\left(\frac12(\alpha-\beta)\right)}$$

en dus tot

$$\frac{\tan\left(\frac12(\alpha+\beta)\right)}{\tan\left(\frac12(\alpha-\beta)\right)}.$$

Daarom

$$\frac{a+b}{a-b}=\frac{\tan\left(\frac12(\alpha+\beta)\right)}{\tan\left(\frac12(\alpha-\beta)\right)}.$$

Opgave 16

Gegeven is driehoek $ABC$ met $a=BC=4$ en $b=AC=3$ en $\gamma=\angle ACB=58^{\rm o}$. De lengte van de hoogtelijn uit $A$ volgt uit $\frac{AC}{AC}=\sin(\gamma)$. Afgerond op twee decimalen is $AV\approx 2{,}54$. Het voetpunt verdeelt zijde $BC$. Uit $\frac{CV}{AC}=\cos(\gamma)$ volgt dat $CV\approx 1{,}59$ en dus is $BV = BC-CV\approx 2{,}41$. Zodoende volgt uit $\frac{AV}{BV}=\tan(\beta)$ dat $\beta\approx 46{,}5^{\rm o}$. Tot slot $\alpha = 180^{\rm o}-58^{\rm o}-46{,}5^{\rm o}=75{,}5^{\rm o}$.

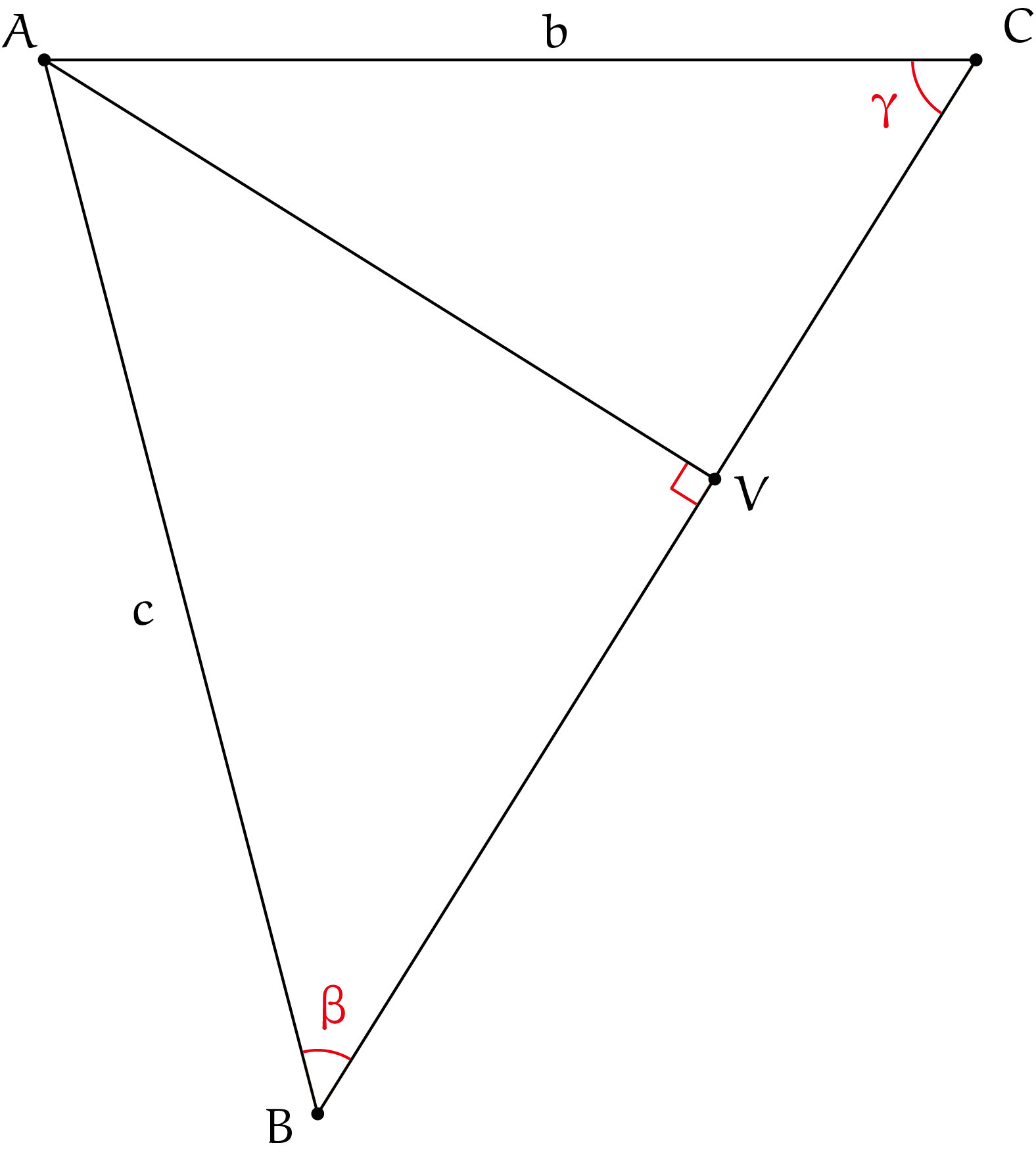
Opgave 17

Omdat $\tan(\beta)=\frac{AV}{BV}$ en $AV = b\cdot\sin(\gamma)$ en $BV=BC-CV=a-b\cdot\cos(\gamma)$, daarom is

$$\tan(\beta)=\frac{b\cdot\sin(\gamma)}{a-b\cdot\cos(\gamma)}.$$