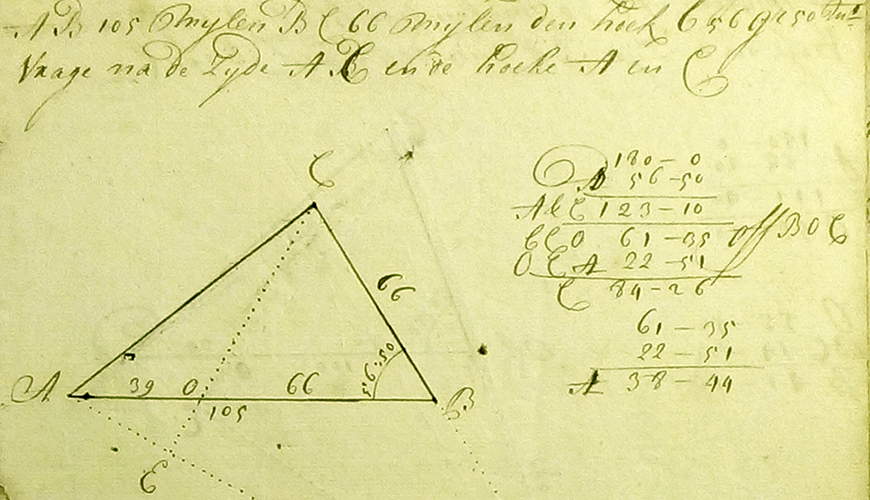
Tangensregel
Naast de bekende sinusregel en cosinusregel bestaat ook de tangensregel. De eerste twee staan, als je in de juiste klas zit, in je wiskundeboek, maar de laatste zul je daar niet meer vinden. In dit artikel wordt de tangensregel weer tevoorschijn gehaald en zie je onder meer wanneer die heel handig is.
De tangensregel is een voorbeeld van een regel die kwam en ging. In de zeventiende eeuw werd de tangensregel bewezen met meetkunde, in de negentiende eeuw met goniometrische verbanden en ergens in de twintigste eeuw werd de tangensregel uit de lesboeken geschrapt.
In dit artikel wordt eerst uitgelegd wat de tangensregel is en hoe je die kunt gebruiken. Daarna komt het zeventiende-eeuwse meetkundige bewijs. Vervolgens komen de goniometrische verbanden aan bod. Tot slot laten we professor Van der Waerden aan het woord over de vraag hoe zinvol het is om al die regels te onthouden.
Sinusregel, Cosinusregel en de tangensregel
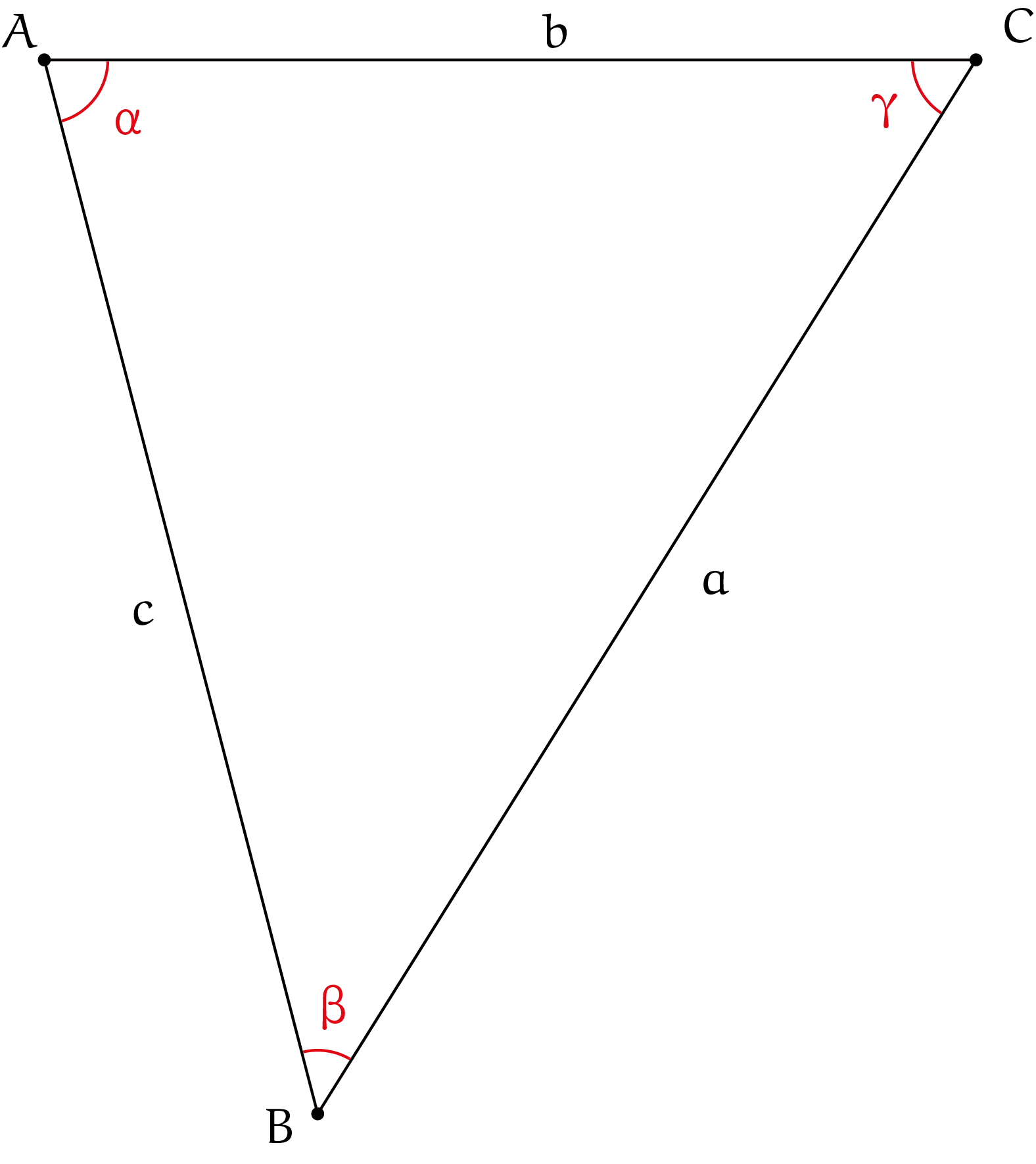
In iedere driehoek $ABC$ met hoekpunten $A$, $B$ en $C$, zijden $a$, $b$ en $c$ en hoeken $\alpha$, $\beta$ en $\gamma$ gelden de sinusregel, cosinusregel en de tangensregel. De eerste twee ken je wellicht:
$$\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}$$
en
$$a^2 = b^2+c^2-2bc\cos(\alpha).$$
De sinusregel heeft een mooi ritme, de cosinusregel heeft iets weg van de stelling van Pythagoras, maar de tangensregel heeft een andere vorm en is minder bekend:
$$\frac{\tan\left(\tfrac{1}{2}(\alpha+\beta)\right)}{\tan\left(\tfrac{1}{2}(\alpha-\beta)\right)}=\frac{a+b}{a-b}.$$
Als je de formule wilt onthouden, focus dan op som en verschil: de tangens van de halve som staat tot de tangens van het halve verschil als de som staat tot het verschil.
Kies de juiste regel
Wiskunde vraagt om de handigheid in iedere situatie snel de juiste formule te kiezen. Ieder van deze drie regels heeft zo zijn eigen toepassing. Hieronder staan enkele situaties. Vraag is welke van de drie regels je het best kunt gebruiken.
Opgave 1Gegeven zijn $a$, $b$ en $\alpha$, met welke regel bereken je $c$, $\beta$ en $\gamma$? Opgave 2Gegeven zijn $b$, $c$ en $\alpha$, met welke regel bereken je $a$? Opgave 3Gegeven zijn $a$, $b$ en $c$, met welke regel bereken je $\alpha$, $\beta$ en $\gamma$? Opgave 4Gegeven zijn $a$, $b$ en $\gamma$, met welke regel bereken je $\alpha$ en $\beta$? |
Toepassing
Wie de tangensregel niet kent zal bij opgave 4 eerst de cosinusregel toepassen om de lengte van zijde $c$ uit te rekenen en daarna de sinusregel voor de hoeken $\alpha$ en $\beta$. Dat kan korter met de tangensregel.
Misschien denk je dat je de tangens in de teller en de noemer niet kunt uitrekenen, maar bedenk dat als de grootte van hoek $\gamma$ gegeven is, dat dan de som van de hoeken $\alpha + \beta$ ook bekend is, want $\alpha + \beta = 180^{\rm o} - \gamma$.
De tangens in de teller kun je dus wel uitrekenen! Kortom, de tangensregel is erg efficiënt wanneer je alleen de onbekende hoeken $\alpha$ en $\beta$ wilt weten. Wanneer je het rekenschema zelf uit wilt vinden, dan kun je aan de slag met de driehoek $ABC$ met $a = BC = 4$, $b = AC = 3$ en $\gamma = \angle ACB = 58^{\rm o}$.
Rekenschema
Straks ga je rekenen, maar het is altijd zinvol om eerst een tekening te maken om de orde van grootte in te schatten. Teken bovenstaande driehoek $ABC$ met $a = 4$, $b = 3$ en $\gamma = 58^{\rm o}$ met potlood op papier of met GeoGebra.
Opgave 5Meet de grootte van de hoeken $\alpha$ en $\beta$ op. Opgave 6Meet ook de lengte van zijde $AB$ op. |
Hieronder staat een rekenschema dat gebaseerd is op een bladzijde uit een anoniem manuscript uit de 17de eeuw dat in het bezit is van Forum Rare Books. De anonieme auteur maakt de volgende stappen. De tangensregel luidt:
$$\frac{\tan\left(\tfrac{1}{2}(\alpha+\beta)\right)}{\tan\left(\tfrac{1}{2}(\alpha-\beta)\right)}=\frac{a+b}{a-b}.$$
Eerst som en verschil berekenen: $a + b = 7$ en $a - b = 1$. Daarna de som van de hoeken $\alpha + \beta = 180^{\rm o} - 58^{\rm o} = 122^{\rm o}$ zodat $(\alpha + \beta) = 61^{\rm o}$ met $\tan\left(\tfrac{1}{2}(\alpha + \beta)\right) = 1{,}8040\ldots$. Je hebt nu drie van de vier onderdelen van de tangensregel uitgerekend en kunt dus de onbekende tangens van het halve verschil uitrekenen: $\tan\left(\tfrac12(\alpha - \beta)\right) = 0{,}2577\ldots$ zodat $(\alpha - \beta) = 14{,}45^{\rm o}$.
Tot slot $\alpha = (\alpha + \beta) + (\alpha - \beta) \approx 74{,}45^{\rm o}$ en $\beta = (\alpha + \beta) - (\alpha - \beta) \approx 46{,}55^{\rm o}$.
Opgave 7Reken zelf het hele rekenschema na en controleer je antwoorden met je tekening. |
Bewijzen
Het aardige van wiskunde is dat je iedere regel kunt bewijzen, dus ook de tangensregel. Op WisFaq en Wikipedia staan bewijzen die gebruik maken van de regels van Simpson over de som of het verschil van twee hoeken. Deze regels krijg je meestal pas in het examenjaar. In die bewijzen wordt geen gebruik gemaakt van twee lijnstukken met lengte $a + b$ en $a - b$. In dit artikel bespreken we een meetkundig bewijs waar die lijnstukken wel in de tekening staan. Dit bewijs is te volgen wanneer je in 3 vwo iets van meetkundig redeneren hebt meegekregen en de goniometrie van de rechthoekige driehoek kent.
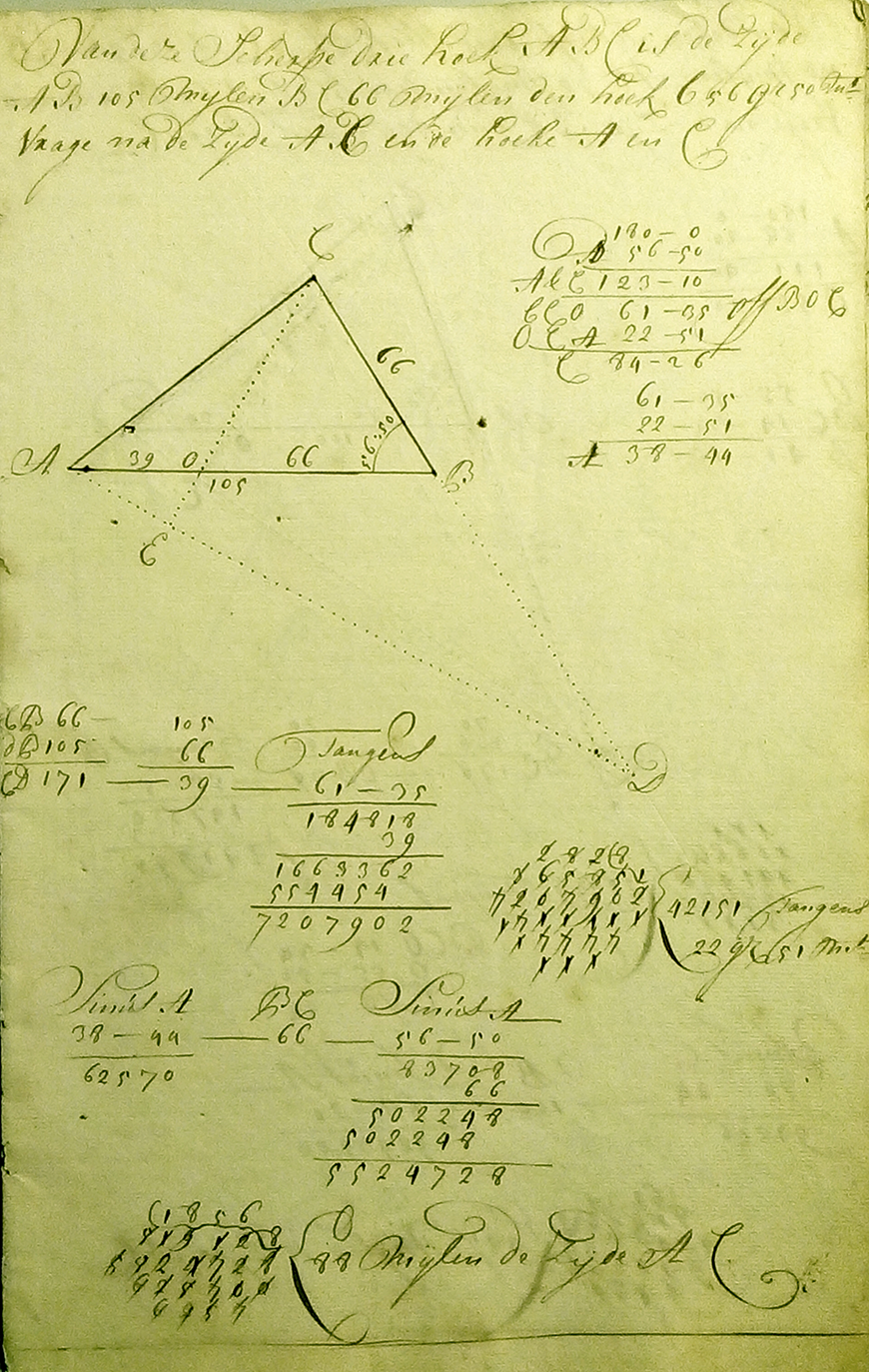
OpdraCht uit het mAnusCript
In figuur 2 zie je een bladzijde uit dat manuscript uit de 17de eeuw. Je ziet de driehoek en alle berekeningen. Gegeven is driehoek $ABC$ met $BC = 66$, $AB = 105$ en $\angle ABC = 56\frac{50}{60}^{\rm o}$.
Opgave 8Bereken met de tangensregel de grootte van de hoeken bij de punten $A$ en $C$. |
Merk op dat de lettering van de punten anders is dan bij de vorige opgave. Gegeven zijn $a$, $c$ en $\beta$. Je kunt in deze situatie de tangensregel herschrijven als
$$\frac{c+a}{c-a}=\frac{\tan\left(\tfrac12(\gamma+\alpha)\right)}{\tan\left(\tfrac12(\gamma-\alpha)\right)}.$$
Invullen geeft $\frac{171}{39}=\frac{\tan\left(61\frac{7}{12}^{\rm o}\right)}{\tan\left(\frac12(\gamma-\alpha)\right)}$.
Afgerond op twee decimalen is $(\gamma - \alpha) \approx 22{,}86^{\rm o}$ zodat $\angle BAC \approx 61\frac{7}{12}^{\rm o} - 22{,}86^{\rm o} = 38{,}73^{\rm o}$ en $\angle BCA\approx 61\frac{7}{12}^{\rm o}+22{,}86^{\rm o} = 84{,}44^{\rm o}$.
MeEtkundig beWijs
In de tekening van het manuscript uit de 17de eeuw zijn hulplijnen getekend. Die hulplijnen construeren twee gelijkbenige driehoeken. Helaas zijn in het manuscript de punten niet zo handig gekozen voor ons doel. Daarom keren we terug naar figuur 3 van driehoek $ABC$ met gegeven zijden $a$, $b$ en hoek $\gamma$. Gemakshalve is $a > b$ waardoor ook $\alpha > \beta$.
We beginnen met een hulplijn. We verlengen lijnstuk $AC$ tot punt $D$ met $BC = CD$ zodat de lengte van $AD$ gelijk is aan $a + b$. Zodoende is driehoek $BCD$ gelijkbenig.

Opgave 9Druk de hoeken van driehoek $BCD$ uit in $\gamma$. |
Lijnstuk $AOE$ is de tweede hulplijn met $AC = CO$, waardoor $BO = a - b$. Zodoende is driehoek $ACO$ ook gelijkbenig.

Opgave 10Druk de hoeken van driehoek $ACO$ uit in $\alpha$ en $\beta$. |
Dankzij deze twee hulplijnen zijn lijnstukken geconstrueerd met lengte $a + b$ en $a - b$, twee hoeken met grootte $\frac12\gamma$ en twee hoeken met grootte $(\alpha + \beta$). Eerst ga je aantonen dat $\angle E$ recht is, vervolgens ga je op zoek naar uitdrukkingen voor $\tan\left(\frac12(\alpha + \beta)\right)$ en $\tan\left(\frac12(\alpha - \beta)\right)$.

Opgave 11Onderzoek driehoek $BEO$ en toon aan dat $\angle E=90^{\rm o}$. Ga daarvoor na in figuur 4 hoe groot $\angle AOC$ is. Opgave 12Toon aan tan $\tan\left(\frac12\alpha + \frac12\beta\right)=\frac{BE}{EO}$. Opgave 13Toon aan dat $\tan\left(\frac12(\alpha-\beta)\right)=\frac{BE}{AE}$. |
De driehoeken $BEO$ en $DEA$ zijn gelijkvormig vanwege die gelijke rechte hoek en die gelijke basishoek $\gamma$ waardoor
$$\frac{AE}{EO}=\frac{AD}{BO}=\frac{a+b}{a-b}.$$
Uit
$$\frac{\tan\left(\frac12(\alpha+\beta)\right)}{\tan\left(\tfrac12(\alpha -\beta)\right)} = \frac{\frac{BE}{EO}}{\frac{BE}{AE}}=\frac{AE}{OE}$$
volgt tot slot het gevraagde, namelijk de tangensregel:
$$\frac{\tan\left(\tfrac{1}{2}(\alpha+\beta)\right)}{\tan\left(\tfrac{1}{2}(\alpha-\beta)\right)}=\frac{a+b}{a-b}.$$
GesChiEdenis
Kort voor 1600 waren wiskundigen op zoek naar nieuwe goniometrische verbanden. Langzaam maar zeker kwamen ze op nieuwe uitdrukkingen. Latijn was toen de wetenschappelijke taal. Uiteindelijk geeft Viète de tangensregel in woorden, maar het is een hele prestatie om in onderstaande zin de moderne uitdrukking te herkennen. Om te beginnen moet je weten dat er voor de tangens nog geen woord was. Viète heeft het over de prosinus!

Rond 1900 verschoof de aandacht van meetkunde naar algebra. Het bewijs voor de tangensregel werd verlegd naar het toepassen van goniometrische regels als de som en verschilregel. Die regels krijg je meestal pas in 6 vwo. Het bewijs slaan we daarom over. Let wel goed op de plus- en mintekens.
$$\begin{matrix}
\sin(\alpha)+\sin(\beta) & = & 2\sin\left(\tfrac12(\alpha+\beta)\right)\cos\left(\tfrac12(\alpha-\beta) \right ) \\
\sin(\alpha)-\sin(\beta) & = & 2\sin\left(\tfrac12(\alpha-\beta)\right)\cos\left(\tfrac12(\alpha+\beta) \right )
\end{matrix}$$
Opgave 14Laat zien dat je de uitdrukking $\frac{a+b}{a-b}$ met de sinusregel kunt herleiden tot de som en het verschil van de sinussen. Opgave 15Pas de som- en verschilregel toe en bewijs zo de tangensregel. |
Kan het simpeler?
In 1930 vroeg Van der Waerden zich af waarom in de schoolboeken de aandacht uitging naar de tangensregel en dat goniometrische bewijs. Zijn standpunt was dat leerlingen wiskunde leren door zelf na te denken over triviale hulplijnen als de
hoogtelijn. Probeer zelf maar.
Opgave 16Ga terug naar de opgave over driehoek $ABC$ met $a=BC=4$, $b=AC=3$ en $\gamma=\angle ACB=58^{\rm o}$. Teken de hoogtelijn uit punt $A$ met voetpunt $V$ op zijde $BC$. Bereken achtereenvolgens de lengte van de zijden van de driehoeken $ACV$ en $ABV$ en tot slot de grootte van de hoek bij de punten $A$ en $B$. Opgave 17Toon nu aan dat $\tan(\beta)=\frac{b\cdot \sin(\gamma)}{a-b\cdot\cos(\gamma)}$. |
ConClusie
De tangensregel is een logische aanvulling op de sinusregel en de cosinusregel. Het aardige is dat juist dat anonieme manuscript duidelijkheid verschafte over de meetkundige redenering achter de tangensregel. Je hebt ontdekt dat er elegante,
ritmische formules zijn, maar ook heb je gezien dat je met hoogtelijnen en de goniometrie van de rechthoekige driehoek net zo ver komt.
| |
||||
| Op de site fransvanschooten.nl/tangensregel.htm staat meer over de tangensregel, waaronder meer voorbeelden uit het genoemde manuscript en meer verwijzingen en details over de geschiedenis. |
|
|||
| |
||||
| Henk Hietbrink gaf vorig schooljaar wiskunde op het Hermann Wesselink College in Amstelveen. Momenteel doet hij onderzoek naar de wiskunde van Simon Stevin, (Vestingbouw en Interest) en verzorgt workshops over zonnewijzers en muqarnas. |
|
|||
Bekijk oplossing
