In zijn werk De methode van de mechanische stellingen (of kortweg De methode) staat een heel bijzonder gedachte-experiment. Om het volume van een bol te vinden, sneed Archimedes die in flinterdunne sneetjes, die hij dan ‘woog’ op een denkbeeldige balans samen met sneetjes van een kegel en van een cilinder. Van kegels en cilinders was het volume hem al bekend. Hieruit leidde hij dan het volume van de bol af. Hoe? Dit bekijken we zo dadelijk in alle details. Maar om deze redenering ten volle te kunnen appreciëren, moet je iets weten over Archimedes’ principe van de balans en over hoe de Oude Grieken over oppervlakten en volumes dachten. 

Principe van de balans

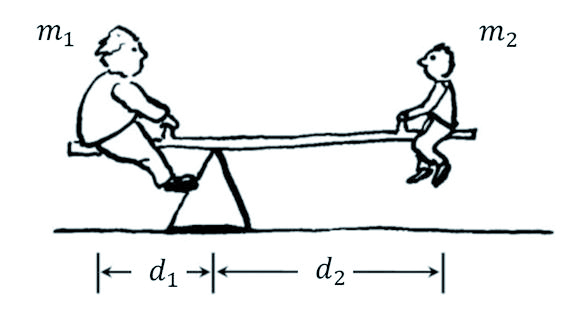
Archimedes was gefascineerd door hefbomen en balansen. Hij formuleerde het principe dat een balans in evenwicht is wanneer het product van de massa en de afstand tot het steunpunt hetzelfde is aan beide kanten van dat steunpunt (figuur $1$). Noemen we de massa’s $m_1$ en $m_2$ en hun afstanden tot het steunpunt $d_1$ en $d_2$, dan geeft dit de formule $d_1\cdot m_1 = d_2\cdot m_2$. In de natuurkunde wordt dit tegenwoordig uitgedrukt met het begrip ‘moment’. Als bijvoorbeeld een vader van $75$ kg en zijn dochter van $25$ kg in een speeltuin op een wipplank spelen, moet de dochter drie keer zo ver van het steunpunt plaatsnemen als de vader om de wipplank in evenwicht te hebben. Het is ook met dat principe dat je kracht kunt zetten met een hefboom of koevoet. Zoals aangehaald in Archimedes en de lauwerkrans (Pythagoras 57-3), schrijft men aan Archimedes in dit verband de uitspraak toe: “Geef mij een steunpunt en ik verplaats de aarde.”

 

Oppervlakte en volume in die tijd

Als iemand je vraagt “Wat is het volume van een kegel?” dan antwoord je wellicht meteen “de oppervlakte van het grondvlak maal de hoogte gedeeld door drie”. Of in formulevorm: $V_{\rm kegel}=\frac{\pi r^2h}{3}.$ Jij en ik bekijken oppervlakten en volumes als zaken die we kunnen uitrekenen door de juiste afmetingen in te vullen in bepaalde formules. Zo bekeken de Oude Grieken het niet! Zij vergeleken altijd twee oppervlakten of twee volumes. Bovendien bekeken ze de figuren zelf als grootheden: ze schreven “de oppervlakte van” of “het volume van” er nooit bij. Ze zeiden bv. “Twee piramides met gelijke grondvlakken verhouden zich tot elkaar zoals hun hoogtes.” Of nog: “een kegel en een cilinder met gelijke grondvlakken en gelijke hoogtes verhouden zich tot elkaar zoals de getallen $1$ en $3$”. Dit verschil in benadering houdt verband met het getalbegrip. Ons begrip reëel getal is geschikt om maatgetallen van willekeurige grootheden weer te geven. Voor de Oude Grieken waren de enige getallen $1, 2, 3, 4, ...$ Verder bestudeerden zij wel verhoudingen van getallen en verhoudingen van grootheden, maar deze verhoudingen zelf werden niet als getallen bekeken.

Het volume van een bol met een denkbeeldige balans

De verhouding van de volumes van een kegel en de omgeschreven cilinder (namelijk $1 : 3$) was al gekend vóór Archimedes. Hij vermeldt dat dit resultaat ontdekt is door Democritos van Abdera (4^e eeuw v.C.) en bewezen door Eudoxos van Knidos (4^e eeuw v.C.).
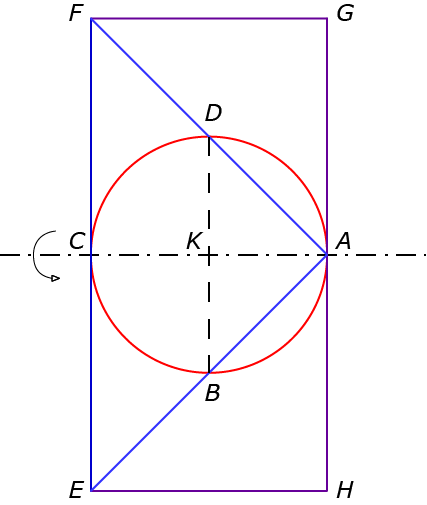
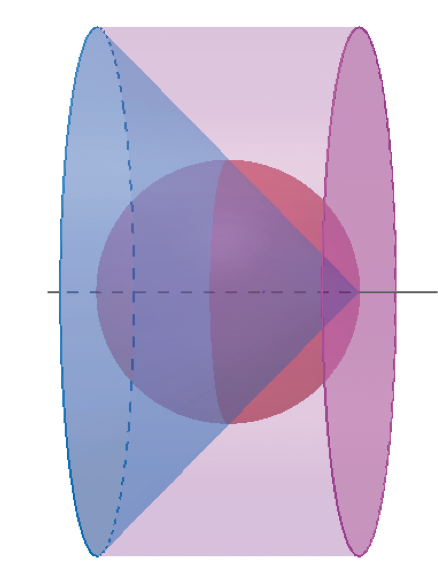
Om hier het volume van een bol uit af te leiden (of liever: de verhouding van het volume van een bol tot het volume van een kegel of een cilinder), gebruikt hij in De methode een denkbeeldige weegschaal waarmee hij deze drie ruimtelichamen met elkaar in balans brengt. We doorlopen deze redenering. Figuur $2a$ is die van Archimedes, maar we hebben de Griekse letters vervangen door Latijnse. Deze figuur moet je in $3$D interpreteren: alles wentelt rond de as $AC$. De cirkel $ABCD$ stelt dus een bol voor, de driehoek $AEF$ een kegel en de rechthoek $EFGH$ een cilinder (zie figuur $2b$).

Opgave 1

Op het einde van de redenering wil Archimedes de verhouding vinden tussen (het volume van) de bol $ABCD$ en (het volume van) de kegel $AEF$. Aan welke verhouding van getallen moet deze verhouding gelijk zijn? Ter herinnering: onze huidige formule voor het volume van een bol met straal $r$ is: $V_{\rm bol}=\frac{4\pi r^3}{3}.$

 

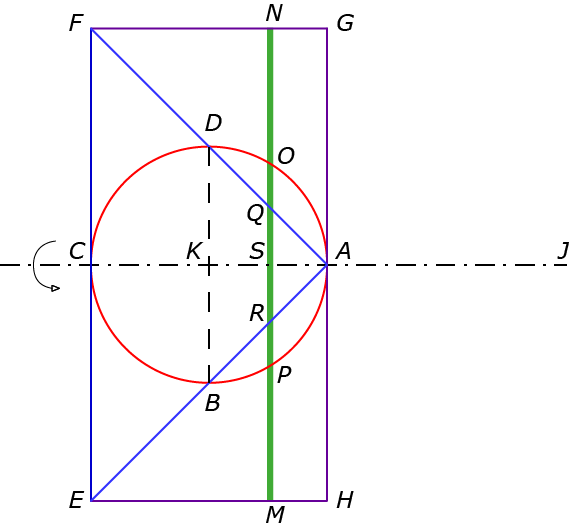
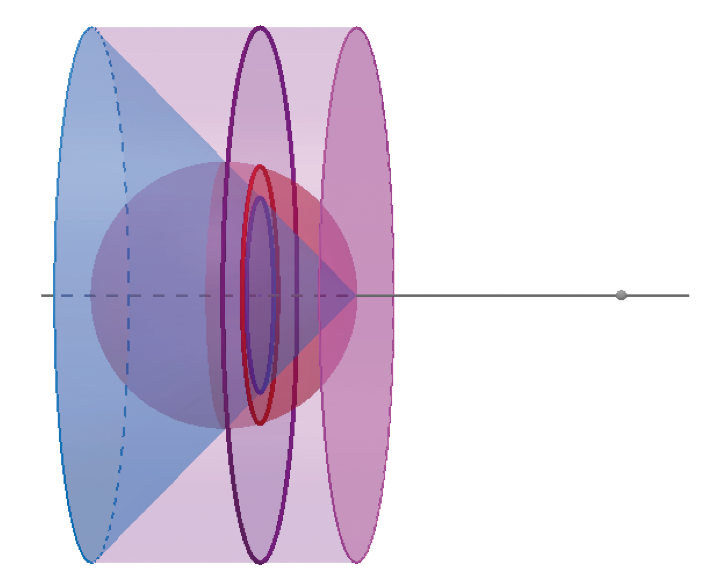
Hij verlengt $AC$ aan de kant van $A$ en hij neemt hierop een punt $J$ zo dat $AJ = CA$. De as $AJ$ bekijkt Archimedes als een balans met steunpunt $A$. Dan neemt hij een willekeurig vlak $MN$ loodrecht op de wentelas $AJ$. De drie lichamen worden gesneden en er ontstaan aldus drie cirkels (zie figuren $3a$ en $3b$).

 

 

 

 

 

 

Opgave 2

Druk de oppervlakten van deze cirkels uit in functie van de straal $r$ van de bol en de afstand $x = AS$ tot het steunpunt $A$.

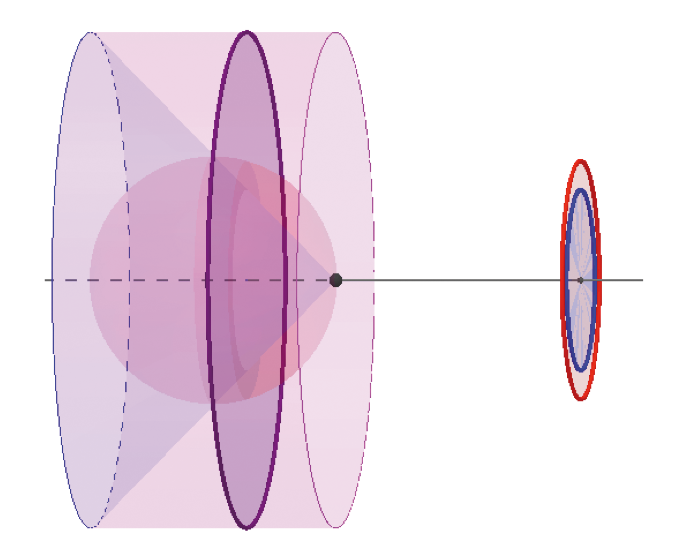
Nu gaat Archimedes deze cirkels wegen op zijn denkbeeldige balans met steunpunt $A$. De snijcirkel van de cilinder laat Archimedes daar staan in het punt $S$; de snijcirkels van de bol en van de kegel verschuift hij naar het punt $J$ (zie figuur $4$). 

Dan toont hij aan dat (de oppervlakten van) deze drie cirkels de balans in evenwicht brengen als je deze oppervlakten als massa’s opvat. Hiermee kleurt Archimedes duidelijk buiten de lijntjes: strikt genomen heeft oppervlakte natuurlijk geen massa... 

 

 

Opgave 3

Reken na dat de balans in evenwicht is. Anders gezegd: dat de formule $d_1 \cdot m_1 = d_2 \cdot m_2$ voldaan is voor $d_1$ gelijk aan de lengte $AS$, $m_1$ gelijk aan de oppervlakte van de cirkel met middellijn $MN$, $d_2$ gelijk aan de lengte $AJ$ en $m_2$ de som van de oppervlakten van de cirkels met middellijnen $OP$ en $QR$.

Dit geldt voor elke dwarsdoorsnede (voor elke waarde van $x$ tussen $0$ en $2r$). Nu beschouwt Archimedes al deze doorsneden samen. Links heeft hij alle dwarsdoorsneden van de cilinder, die hij vervangt door het volume van de cilinder in het zwaartepunt $K$. Rechts heeft hij alle dwarsdoorsneden van de kegel en van de bol, allemaal in dat ene punt $J$. Hij vervangt ze door de som van de volumes van de bol en de kegel, in $J$. Uit het evenwicht van de sneetjes besluit hij dat deze volumes nu in evenwicht zijn. Ook weer een gewaagde gedachte, die vooruitloopt op wat in de 17^e eeuw de integraalrekening zal worden: een volume kan gezien worden als een ‘som’ (integraal) van oneindig veel oppervlaktes... 

Uit het evenwicht van aan de ene kant (het volume van) de cilinder opgehangen in $K$ en aan de andere kant de som van (de volumes van) de kegel en de bol opgehangen in $J$ leidt hij af dat de verhouding van (het volume van) de bol tot (het volume van) de kegel de gewenste verhouding is (die je vond in opgave $1$).

Opgave 4

Ga dit na.

Hiermee is deze mooie redenering afgerond.

Hieruit de oppervlakte van de bol

De kleinere kegel $ABD$, die in de bol zit, heeft als volume één achtste van dat van de grote kegel $AEF$. Dus volgt uit opgave $4$ dat het volume van de bol gelijk is aan vier keer dat van de kegel $ABD$. Dit laat Archimedes vermoeden: “De oppervlakte van de bol moet gelijk zijn aan vier keer de oppervlakte van het grondvlak van deze kleine kegel $ABD$. Ik heb immers de intuïtie dat, aangezien elke cirkel gelijk is aan de driehoek met als basis de omtrek van de cirkel en als hoogte de straal, elke bol ook gelijk moet zijn aan de kegel met als grondvlak de oppervlakte van de bol en als hoogte de straal.” Is dit louter analogie of bekijkt Archimedes de bol als opgedeeld in kleine ‘kegels’? Als je immers de oppervlakte van de bol verdeelt in heel veel kleine stukjes, dan kun je de bol bekijken als samengesteld uit kleine ‘kegels’ waarvan de grondvlakken bijna vlak zijn en met als hoogte ongeveer de straal $r$ van de bol. De methode eindigt met dit vermoeden over de oppervlakte van een bol.

Bewijs zonder balans

Later in een ander werk, De bol en de cilinder, zal Archimedes dit vermoeden bewijzen. Dit doet hij met een zuiver meetkundig bewijs dat past in de euclidische traditie. Daarna bewijst hij, hierop steunend, zijn bevinding over het volume van een bol die hij in De methode met een denkbeeldige balans had ontdekt. 

De redenering met de balans beschouwt Archimedes als een trucje om het resultaat te vinden, maar niet als een volwaardig wiskundig bewijs. Het mengen van wiskunde met ideeën uit de mechanica past niet binnen het euclidische systeem van die tijd. Bovendien steunt de redenering op een dimensiesprong: uit verbanden tussen oppervlakten van doorsneden wordt een verband tussen volumes afgeleid. Het is een toepassing avant la lettre van wat in de zeventiende eeuw het principe van Cavalieri (Bonaventura Cavalieri, 17^e eeuw) en de integraalrekening (Isaac Newton, 17^e eeuw; Gottfried Wilhelm Leibniz, 17^e eeuw) zullen worden. Archimedes was zijn tijd vooruit!

Palimpsest

Archimedes stuurde zijn papyrusrol met De methode naar de beroemde bibliotheek van Alexandrië (in het huidige Egypte). Later werd het werk overgeschreven op perkamenten vellen zodat het beter bewaard kon worden. De vellen werden ingebonden tot een boekje, een codex. De codex waarin De methode en enkele andere werken van Archimedes opgenomen zijn, verdween en werd pas in 1906 in een klooster in Jeruzalem teruggevonden. In de 13^e eeuw hadden de monniken oorspronkelijke teksten en tekeningen van Archimedes afgeschraapt om er gebeden op te schrijven. De codex van Archimedes was een palimpsest geworden, een hergebruikt stuk perkament. De codex werd in de loop van de twintigste eeuw gestolen en dook in 1998 weer op in een verkoopzaal waar het per opbod werd verkocht. Een mysterieuze Mr. B deed het hoogste bod en kocht het aan voor 2.200.000 dollar. Niemand weet wie Mr. B is, al bestaan er wel speculaties. Gelukkig laat hij toe dat wetenschappers het werk met de modernste methoden bestuderen. 

Over de avontuurlijke geschiedenis van deze codex is een mooi boek geschreven: De Archimedes-codex, de geheimen van een opzienbarende palimpsest ontsluierd, door R. Netz en W. Noel.

 

Bekijk oplossing