Het artikel Mok = donut uit Pythagoras 61-4 is de voorganger van dit artikel. Het is makkelijker als je dat artikel ook hebt gelezen. Als je intuïtief begrijpt wat een oppervlak is en wat de Eulerkarakteristiek en het genus van een oppervlak zijn, dan is dit artikel ook prima te begrijpen. Voor de zekerheid: de Eulerkarakteristiek is een getal kenmerkend voor een oppervlak; zo is die van een sfeer gelijk aan $2$ en die van een donut $0$. Het genus van een oppervlak is het aantal gaten van een oppervlak. Hier later meer over.

We zullen allereerst het idee van 'behaarde oppervlakken' vertalen in wiskunde, namelijk oppervlakken met daarop pijltjes, of nog formeler: oppervlakken met een vectorveld. Daarna zullen we kijken naar punten in de beharing waar de beharing niet netjes zit. Denk aan de kruin: het kale plekje midden in het haar dat sommige mensen hebben. Wiskundig verstaan we dat als singulariteiten van de vectorvelden. Als laatst kijken we naar een belangrijke stelling uit de topologie: de Poincaré-Hopf stelling. Deze stelling kan worden gebruikt om te bepalen of een vectorveld op een oppervlak singulariteiten moet bevatten, oftewel: of de beharing op een oppervlak netjes plat te kammen is of niet.

Vectorveld op oppervlak

Beharing en vectorvelden

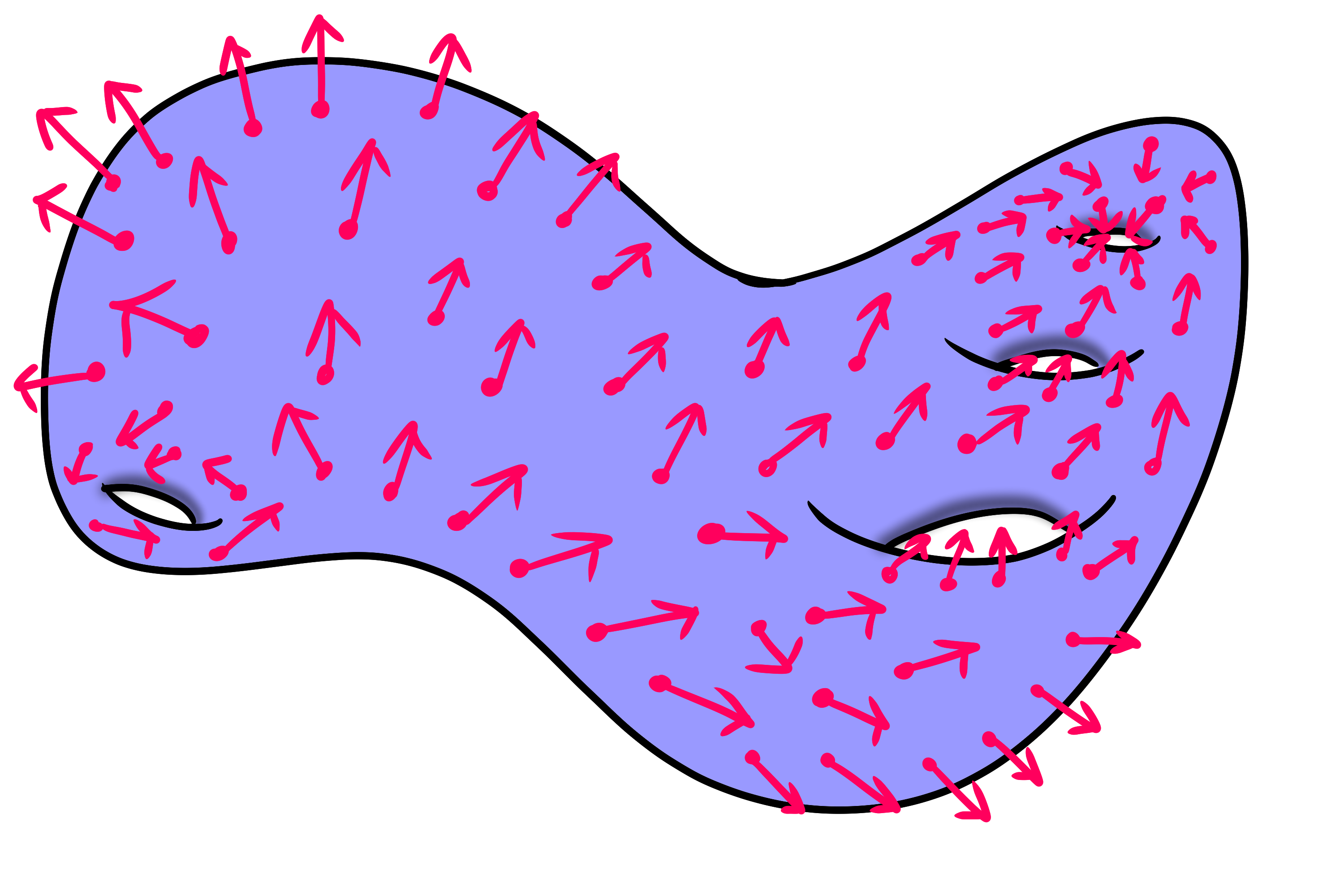
Laten we eens bekijken wat nou wordt bedoeld met 'behaarde oppervlakken'. Wiskundigen staan wel bekend als gebruikers van creatieve namen, maar hier is toch echt meer serieuze terminologie voor bedacht: een vectorveld op een oppervlak. Een vectorveld op een oppervlak is een verzameling vectoren of pijlen op dat oppervlak: aan elk punt van het oppervlak bevestigen we een pijl, zie figuur 1.

Laten we nu eens kijken wat het betekent om de haren op een oppervlak plat te kammen. Het platkammen van haren op een oppervlak betekent eigenlijk dat we de vectoren op het oppervlak 'plat' kammen. Maar wat bedoelen we met 'plat'? We noemen een vector plat als deze het oppervlak raakt in het punt waar hij aan het oppervlak vastzit. Dit is zoiets als de raaklijn van een kromme, deze raakt de kromme in een zeker punt, wat betekent dat hij lokaal plat lijkt te liggen op de kromme. Een vectorveld waarbij elke vector plat op het oppervlak ligt heet een raakvectorveld. Zie figuur 2 voor een voorbeeld van een raakvectorveld op een oppervlak.

Platgekamd vectorveld op oppervlak

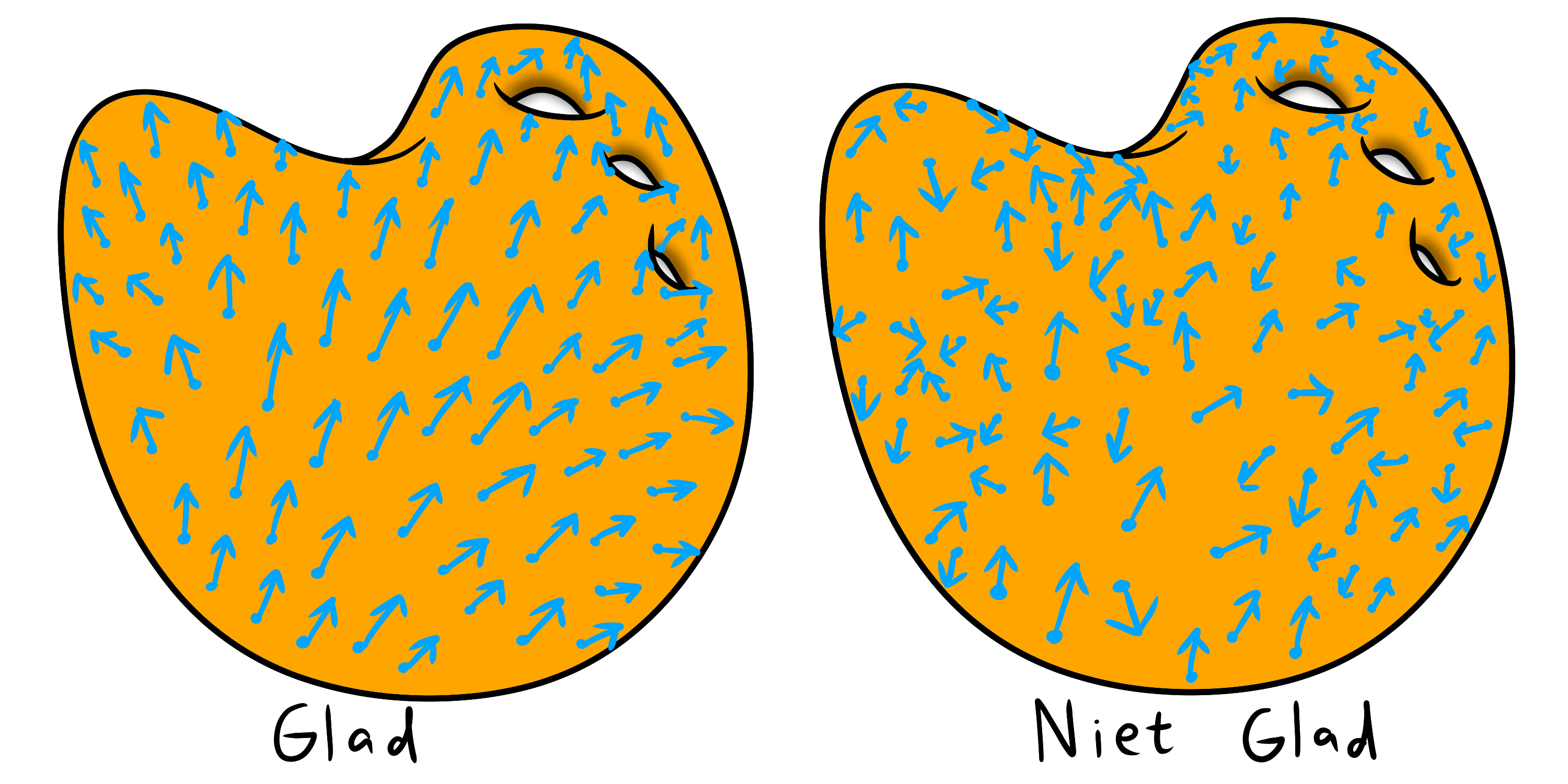
Uiteindelijk gaat het dan om het platkammen van haren op een oppervlak in een 'vloeiende' beweging. In de wiskunde heet een raakvectorveld op een oppervlak dat op vloeiende wijze is plat gekamd een glad raakvectorveld. Dit betekent grof gezegd dat de vectoren op punten die dicht bij elkaar liggen in dezelfde richting wijzen. Zodra je punten bekijkt die verder uit elkaar liggen kunnen de vectoren ook geleidelijk een andere richting op wijzen. 

Zie figuur 3 voor een voorbeeld van een glad en niet-glad raakvectorveld.

Een glad versus een niet-glad raakvectorveld

Singulariteit en index

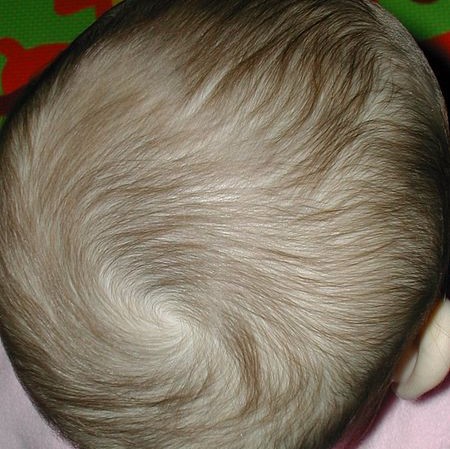
Singulariteit in het kapsel van een baby

Maar wanneer gaat het nou 'fout' tijdens het platkammen van haren op een oppervlak in een vloeiende beweging? Wiskundig geformuleerd: hoe definiëren we punten op een oppervlak waarop een raakvectorveld 'niet bestaat'? Met 'niet bestaat' bedoelen we zoiets als de vector op dat punt moet een lengte van $0$ hebben en dat is afwijkend omdat we een behaard oppervlak bekijken en dus eigenlijk alle haren van lengte ongelijk aan $0$ willen hebben. Dit soort punten op een oppervlak noemen we ook wel singulariteiten van het gladde raakvectorveld. Zie als voorbeeld het kapsel van de baby in figuur 4 uit het Wikipedia-artikel over de Hairy ball theorem. Hier is een 'kaal' plekje te zien in het midden van de spiraal van haren, een singulariteit van het kapsel.

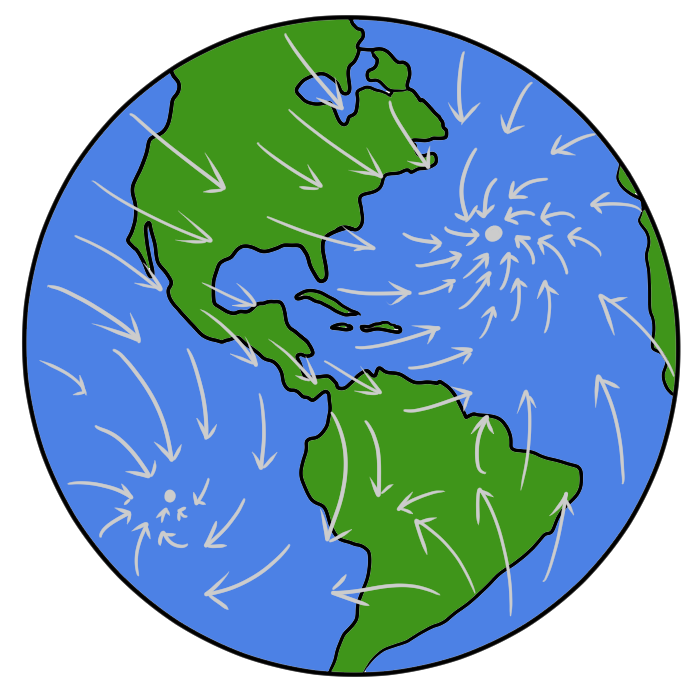
Waarom zijn we geïnteresseerd in singulariteiten? Dit zijn punten van vectorvelden waar bijzonder gedrag te zien is. Vectoren geven vaak de richtingen van beweging aan en singulariteiten kunnen punten zijn waar veel beweging naartoe is of juist veel beweging vanaf komt. Denk bijvoorbeeld aan het oog van een orkaan waarbij vectoren de windrichtingen aangeven, het oppervlak is in dit geval het oppervlak van onze planeet. Er is veel wind om het oog heen, maar in het oog is het nagenoeg windstil, dus daar hebben we te maken met een singulariteit in het gladde raakvectorveld van windrichtingen. Singulariteiten kunnen diverse vormen aannemen, zie figuur 5 voor een aantal voorbeelden.

Diverse voorbeelden van singulariteiten op vectorvelden

We kunnen singulariteiten zelfs onderscheiden op basis van hoe 'grillig' ze zijn. Met 'grillig' bedoelen we dan grof gezegd de hoeveelheid beweging in diverse richtingen rond de singulariteit. Dergelijke grilligheid van een singulariteit kunnen we berekenen en dat noemen we dan de index van de singulariteit. Als $p$ een singulariteit op een oppervlak met glad raakvectorveld is, dan zullen we de index noteren als $Index(p)$.

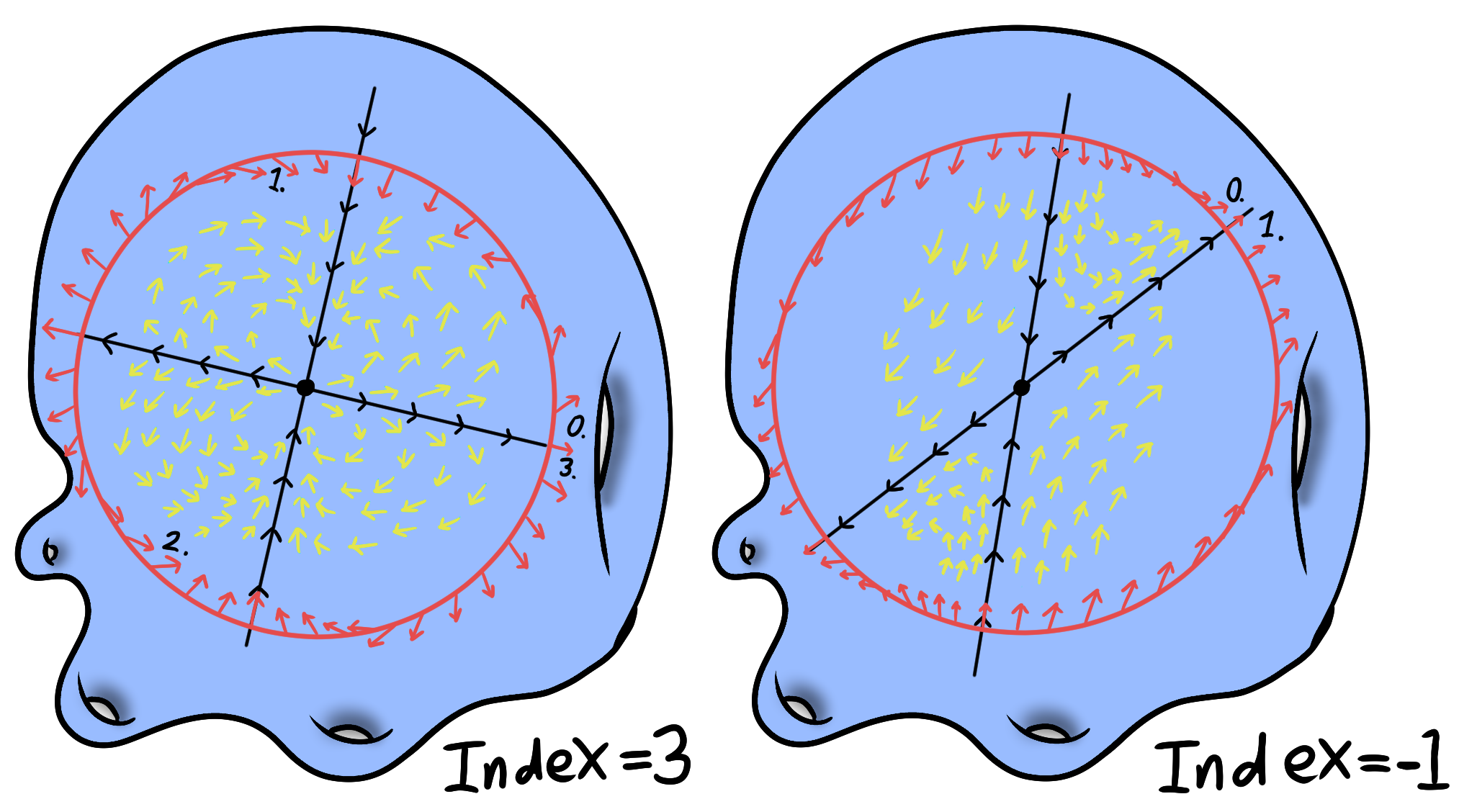
De index van een singulariteit zal op een glad raakvectorveld altijd een geheel getal zijn, positief of negatief, en we kunnen dit getal berekenen door te tellen hoe vaak het vectorveld om de singulariteit heen draait. Wat concreter: teken een cirkel om een singulariteit, maar wel zo dat de cirkel enkel die singulariteit bevat (een glad raakvectorveld op een oppervlak kan meerdere singulariteiten bevatten). Loop nu tegen de klok in over deze cirkel en hou steeds bij in welke richting te pijlen staan op de punten op de cirkel. Nu bereken je de singulariteit door te tellen hoe vaak de pijlen tegen de klok in draaien (of met de klok mee draaien, maar dan tel je ze als negatief). Een plaatje zegt natuurlijk meer dan duizend woorden, dus laten we naar een aantal voorbeelden kijken in figuur 6. Probeer ook zelf eens na te gaan dat een bron en een put beide index 1 hebben.

Twee voorbeelden waarin we de index bepalen. Bij de linker singulariteit draait het vectorveld drie keer tegen de klok in om de singulariteit, dus de index is $3$.  Evenzo bepalen we bij de rechter singulariteit een index $-1$.

PoinCarÉ-Hopf stelling

Nu hebben we alle puzzelstukjes verzameld die nodig zijn voor het formuleren van de Poincaré-Hopf stelling. Voor een oppervlak $M$ met een glad raakvectorveld zullen we de verzameling van singulariteiten noteren als $S(M)$.

 

	Stelling
		(Poincaré-Hopf stelling): Zij $M$ een oppervlak met een glad raadvectorveld. Dan geldt de volgende formule: $$\sum_{p \in S(M)}Index(p)=\chi(M)$$ waarbij $\chi(M)$ de Eulerkarakteristiek is van het oppervlak $M$.

Oke, maar waarom is dit interessant? Als we voor elke singulariteit van een glad raakvectorveld op een oppervlak $M$ de index bepalen en we tellen die op, dan is dat blijkbaar gelijk aan de Eulerkarakteristiek van het oppervlak? Nou dit is heel interessant! Allereerst, op een oppervlak bestaan er ontelbaar veel verschillende gladde raakvectorvelden. Maar blijkbaar maakt het niet uit welke je hebt, als je de singulariteiten vaststelt, de indices berekent en die bij elkaar optelt, dan krijg je altijd hetzelfde getal: de Eulerkarakteristiek. De Eulerkarakteristiek hangt immers enkel af van het oppervlak en niet van het vectorveld op dat oppervlak. Om terug naar de behaarde objecten te gaan, laten we maar direct kijken wat deze stelling daarover zegt.

Wel of geen kale plekjes?

Zoals gezegd kunnen we de haren op een behaard oppervlak in een vloeiende wijze platkammen en dan krijgen we iets wat hetzelfde is als een glad raakvectorveld aan dat oppervlak. Voor die platgekamde haren en dus het gladde raakvectorveld weten we dat de Poincaré-Hopf stelling waar is. Dus wat zijn dan de implicaties? Wellicht herinner je je van het Mok = donut artikel dat de Eulerkarakteristiek van een sfeer (buitenkant van bol) gelijk is aan $2$, dus ook van een kokosnoot. Wat de Poincaré-Hopf stelling nu zegt: het maakt niet uit hoe je de haren op de kokosnoot vloeiend platkamt, de som van de indices van de singulariteiten is gelijk aan $\chi({\rm kokosnoot}) = 2$. Wat zegt dit? Nou, de som van indices zou gelijk zijn aan $0$ als er geen singulariteiten zouden zijn in het vloeiend platgekamde haren vectorveld, maar de som is gelijk aan $2$ zoals Poincaré-Hopf zegt, dus er moeten wel singulariteiten zijn! Anders gezegd: het maakt niet uit op welke vloeiende wijze je de haren op een kokosnoot platkamt, je krijgt sowieso een 'kale' plek tussen de platgekamde haren, denk bijvoorbeeld aan de haren op het babyhoofd van figuur 4.

Twee singulariteiten op in het gladde raakvectorveld van windrichtingen op onze planeet, waar het windstil is

Zoals gezegd zijn windrichtingen op onze planeet ook een glad raakvectorveld aan het oppervlak van onze planeet (en dat oppervlak is een sfeer). De Poincaré-Hopf stelling zegt dat er tenminste één punt moet zijn waar het windstil is: er moet immers tenminste één singulariteit in het raakvectorveld van windrichtingen zijn op het oppervlak van de aarde, zie figuur 7.

Behaarde donut zonder singulariteiten

Het wordt nog interessanter. Wellicht weet je van het Mok = donut artikel nog dat de Eulerkarakteristiek $\chi(M)$ van een oppervlak $M$ gerelateerd is aan het aantal gaten of ook wel het genus $g(M)$ van dat oppervlak via de volgende vergelijking: $\chi(M) = 2 - 2g(M)$. Wat zegt dit? Nou, neem bijvoorbeeld een donut, die heeft één gat, dus genus $g({\rm donut}) = 1$. Zo weten we, door $\chi({\rm donut}) = 2 - 2g({\rm donut}) = 2 - 2 \cdot 1 = 0$, dat een donut Eulerkarakteristiek $0$ heeft. Wat zegt de Poincaré-Hopf stelling nu? Wel, de som van de indices van singulariteiten op een donut moet gelijk zijn aan $0$. Dit betekent nog niet dat we haren op een donut plat kunnen kammen zonder kale plekjes: indices van verschillende singulariteiten kunnen immers tegen elkaar wegvallen. We zien echter in figuur 8 dat het mogelijk is.

En een krakeling? Die heeft genus $g({\rm krakeling}) = 3$, dus $\chi({\rm krakeling}) = 2 - 2g({\rm krakeling}) = 2 - 2 \cdot 3 = -4$. Volgens Poincaré-Hopf is het op een krakeling dus niet mogelijk om haren
op een vloeiende wijze plat te kammen zonder kale plekjes te creëren. En zo kunnen we doorgaan voor een hoop andere behaarde gebakjes!